Table of Contents

Dimensionality Reduction

Dimensionality Reduction

Dimensionality Reduction is the process of reducing the number of random variables under consideration by obtaining a set of principal variables. It can be divided into feature selection and feature extraction.

Dimensionality Reduction Methods:

t-SNE | T-distributed Stochastic Neighbor Embeddings

Understanding t-SNE Part 1: SNE algorithm and its drawbacks
Understanding t-SNE Part 2: t-SNE improvements over SNE
t-SNE (statwiki)
t-SNE tutorial (video)
series (deleteme)

SNE - Stochastic Neighbor Embeddings:
SNE is a method that aims to match distributions of distances between points in high and low dimensional space via conditional probabilities.
It Assumes distances in both high and low dimensional space are Gaussian-distributed.

t-SNE:
t-SNE is a machine learning algorithm for visualization developed by Laurens van der Maaten and Geoffrey Hinton.
It is a nonlinear dimensionality reduction technique well-suited for embedding high-dimensional data for visualization in a low-dimensional space of two or three dimensions.
Specifically, it models each high-dimensional object by a two- or three-dimensional point in such a way that similar objects are modeled by nearby points and dissimilar objects are modeled by distant points with high probability.

It tends to preserve local structure, while at the same time, preserving the global structure as much as possible.


Stages:

  1. It Constructs a probability distribution over pairs of high-dimensional objects in such a way that similar objects have a high probability of being picked while dissimilar points have an extremely small probability of being picked.
  2. It Defines a similar probability distribution over the points in the low-dimensional map, and it minimizes the Kullback–Leibler divergence between the two distributions with respect to the locations of the points in the map.

Key Ideas:
It solves two big problems that SNE faces:

  1. The Crowding Problem:
    The “crowding problem” that are addressed in the paper is defined as: “the area of the two-dimensional map that is available to accommodate moderately distant datapoints will not be nearly large enough compared with the area available to accommodate nearby datepoints”. This happens when the datapoints are distributed in a region on a high-dimensional manifold around i, and we try to model the pairwise distances from i to the datapoints in a two-dimensional map. For example, it is possible to have 11 datapoints that are mutually equidistant in a ten-dimensional manifold but it is not possible to model this faithfully in a two-dimensional map. Therefore, if the small distances can be modeled accurately in a map, most of the moderately distant datapoints will be too far away in the two-dimensional map. In SNE, this will result in very small attractive force from datapoint i to these too-distant map points. The very large number of such forces collapses together the points in the center of the map and prevents gaps from forming between the natural clusters. This phenomena, crowding problem, is not specific to SNE and can be observed in other local techniques such as Sammon mapping as well.
    • Solution - Student t-distribution for \(q\):
      Student t-distribution is used to compute the similarities between data points in the low dimensional space \(q\).
  2. Optimization Difficulty of KL-div:
    The KL Divergence is used over the conditional probability to calculate the error in the low-dimensional representation. So, the algorithm will be trying to minimize this loss and will calculate its gradient:

    $$\frac{\delta C}{\delta y_{i}}=2 \sum_{j}\left(p_{j | i}-q_{j | i}+p_{i | j}-q_{i | j}\right)\left(y_{i}-y_{j}\right)$$

    This gradient involves all the probabilities for point \(i\) and \(j\). But, these probabilities were composed of the exponentials. The problem is that: We have all these exponentials in our gradient, which can explode (or display other unusual behavior) very quickly and hence the algorithm will take a long time to converge.

    • Solution - Symmetric SNE:
      The Cost Function is a symmetrized version of that in SNE. i.e. \(p_{i\vert j} = p_{j\vert i}\) and \(q_{i\vert j} = q_{j\vert i}\).

Application:
It is often used to visualize high-level representations learned by an artificial neural network.

Motivation:
There are a lot of problems with traditional dimensionality reduction techniques that employ feature projection; e.g. PCA. These techniques attempt to preserve the global structure, and in that process they lose the local structure. Mainly, projecting the data on one axis or another, may (most likely) not preserve the neighborhood structure of the data; e.g. the clusters in the data:
img
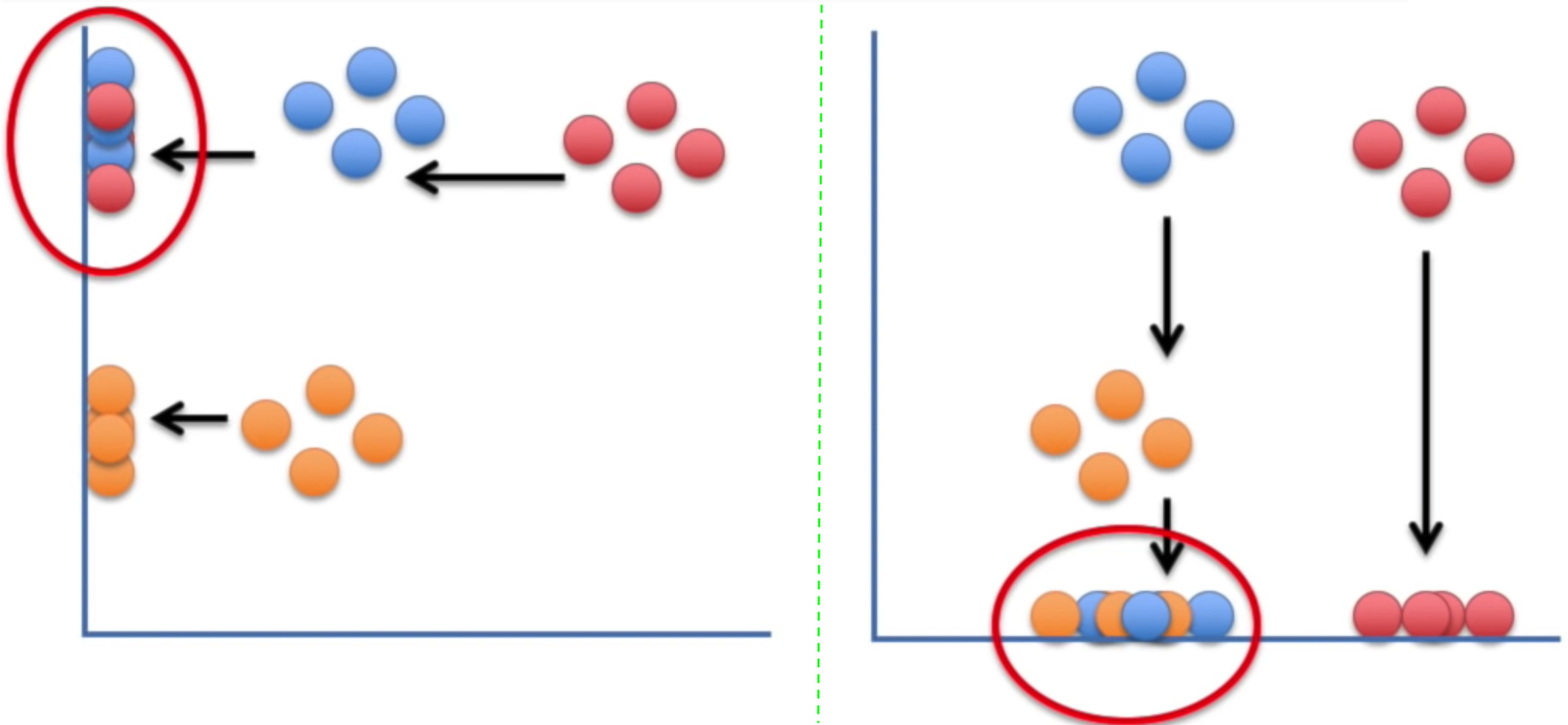
t-SNE finds a way to project data into a low dimensional space (1-d, in this case) such that the clustering (“local structure”) in the high dimensional space is preserved.

t-SNE Clusters:
While t-SNE plots often seem to display clusters, the visual clusters can be influenced strongly by the chosen parameterization and therefore a good understanding of the parameters for t-SNE is necessary. Such “clusters” can be shown to even appear in non-clustered data, and thus may be false findings.
It has been demonstrated that t-SNE is often able to recover well-separated clusters, and with special parameter choices, approximates a simple form of spectral clustering.

Properties:

Algorithm:


Issues/Weaknesses/Drawbacks:

  1. The paper only focuses on the date visualization using t-SNE, that is, embedding high-dimensional date into a two- or three-dimensional space. However, this behavior of t-SNE presented in the paper cannot readily be extrapolated to \(d>3\) dimensions due to the heavy tails of the Student t-distribution.
  2. It might be less successful when applied to data sets with a high intrinsic dimensionality. This is a result of the local linearity assumption on the manifold that t-SNE makes by employing Euclidean distance to present the similarity between the datapoints.
  3. The cost function is not convex. This leads to the problem that several optimization parameters (hyperparameters) need to be chosen (and tuned) and the constructed solutions depending on these parameters may be different each time t-SNE is run from an initial random configuration of the map points.
  4. It cannot work “online”. Since it learns a non-parametric mapping, which means that it does not learn an explicit function that maps data from the input space to the map. Therefore, it is not possible to embed test points in an existing map. You have to re-run t-SNE on the full dataset.
    A potential approach to deal with this would be to train a multivariate regressor to predict the map location from the input data.
    Alternatively, you could also make such a regressor minimize the t-SNE loss directly (parametric t-SNE).


t-SNE Optimization:


Discussion and Information:


Feature Selection

Feature Selection

Feature Selection is the process of selecting a subset of relevant features (variables, predictors) for use in model construction.

Applications:

Strategies/Approaches:


Correlation Feature Selection

The Correlation Feature Selection (CFS) measure evaluates subsets of features on the basis of the following hypothesis:
“Good feature subsets contain features highly correlated with the classification, yet uncorrelated to each other”.

The following equation gives the merit of a feature subset \(S\) consisting of \(k\) features:

$${\displaystyle \mathrm {Merit} _{S_{k}}={\frac {k{\overline {r_{cf}}}}{\sqrt {k+k(k-1){\overline {r_{ff}}}}}}.}$$

where, \({\displaystyle {\overline {r_{cf}}}}\) is the average value of all feature-classification correlations, and \({\displaystyle {\overline {r_{ff}}}}\) is the average value of all feature-feature correlations.

The CFS criterion is defined as follows:

$$\mathrm {CFS} =\max _{S_{k}}\left[{\frac {r_{cf_{1}}+r_{cf_{2}}+\cdots +r_{cf_{k}}}{\sqrt {k+2(r_{f_{1}f_{2}}+\cdots +r_{f_{i}f_{j}}+\cdots +r_{f_{k}f_{1}})}}}\right]$$


Feature Selection Embedded in Learning Algorithms


Information Theory Based Feature Selection Mechanisms

There are different Feature Selection mechanisms around that utilize mutual information for scoring the different features.
They all usually use the same algorithm:

  1. Calculate the mutual information as score for between all features (\({\displaystyle f_{i}\in F}\)) and the target class (\(c\))
  2. Select the feature with the largest score (e.g. \({\displaystyle argmax_{f_{i}\in F}(I(f_{i},c))}\)) and add it to the set of selected features (\(S\))
  3. Calculate the score which might be derived form the mutual information
  4. Select the feature with the largest score and add it to the set of select features (e.g. \({\displaystyle {\arg \max }_{f_{i}\in F}(I_{derived}(f_{i},c))}\))
  5. Repeat 3. and 4. until a certain number of features is selected (e.g. \({\displaystyle \vert S\vert =l}\))

Feature Extraction

Feature Extraction

Feature Extraction starts from an initial set of measured data and builds derived values (features) intended to be informative and non-redundant, facilitating the subsequent learning and generalization steps, and in some cases leading to better human interpretations.

In dimensionality reduction, feature extraction is also called Feature Projection, which is a method that transforms the data in the high-dimensional space to a space of fewer dimensions. The data transformation may be linear, as in principal component analysis (PCA), but many nonlinear dimensionality reduction techniques also exist.

Methods/Algorithms:


Data Imputation

Resources:

Outliers
Replacing Outliers
Data Transformation - Outliers - Standardization
PreProcessing in DL - Data Normalization
Imputation and Feature Scaling
Missing Data - Imputation
Dim-Red - Random Projections
F-Selection - Relief
Box-Cox Transf - outliers
ANCOVA
Feature Selection Methods