Mathematical Background

1. Maps:

   We reserve the term map to refer to vector-valued functions. That is, maps are functions which return more than a single value.

2. Graph:
   Consider a function \(f : \mathbf{R}^n \rightarrow \mathbf{R}\).
   The graph of \(f\) is the set of input-output pairs that \(f\) can attain, that is: \(G(f) := \left \{ (x,f(x)) \in \mathbf{R}^{n+1} : x \in \mathbf{R}^n \right \}.\)
   

   It is a subset of \(\mathbf{R}^{n+1}\).

3. Epigraph:
   Consider a function \(f : \mathbf{R}^n \rightarrow \mathbf{R}\).
   The epigraph, denoted \(\mathop{\bf epi} f\), describes the set of input-output pairs that \(f\) can achieve, as well as “anything above”:
   \(\mathop{\bf epi} f := \left \{ (x,t) \in \mathbf{R}^{n+1} ~:~ x \in \mathbf{R}^n, \ \ t \ge f(x) \right \}.\)

   epi in Greek means “above”

   Example [image]

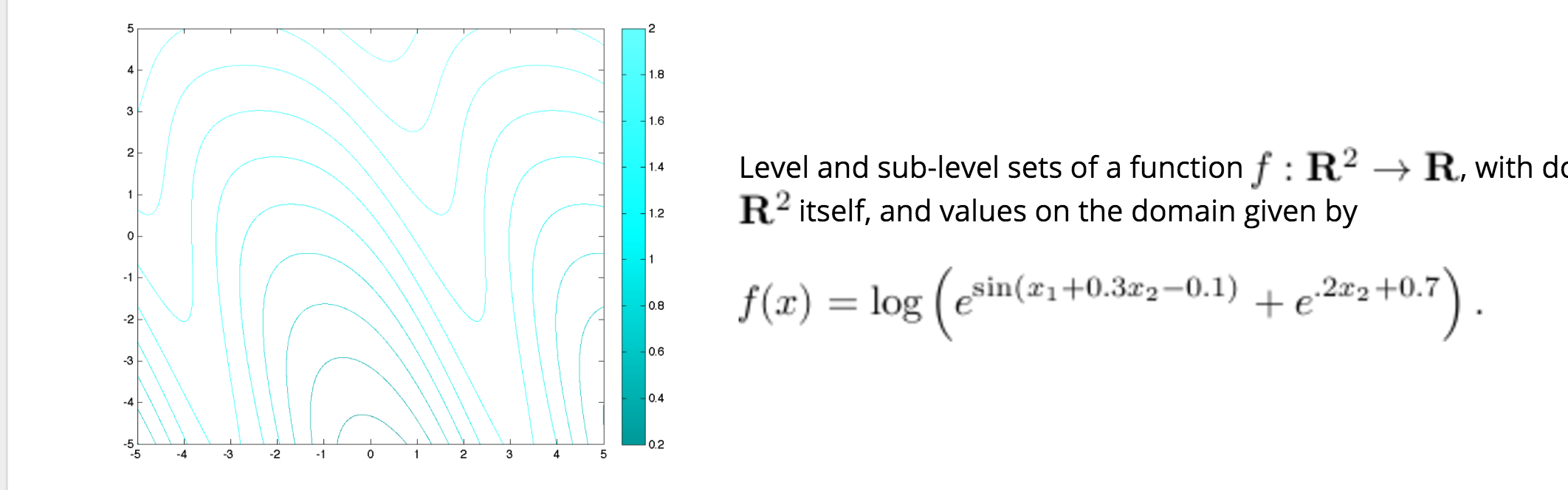
4. Level and Sub-level Sets:
   

   Level and sub-level sets correspond to the notion of contour of a function. Both are indexed on some scalar value \(t\).

   • Level sets: is simply the set of points that achieve exactly some value for the function \(f\).
     For \(t \in \mathbf{R}\), the \(t-\)level set of the function \(f\) is defined as:
     \(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{L}_t(f) := \left\{ x \in \mathbf{R}^{n} ~:~ x \in \mathbf{R}^n, \ \ t = f(x) \right \}.\)

   • Sub-level sets: is the set of points that achieve at most a certain value for \(f\), or below:
     \(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{S}_t(f) := \left\{ x \in \mathbf{R}^{n} ~:~ x \in \mathbf{R}^n, \ \ t \ge f(x) \right\}.\)

   Example [image]

Mathematical Formulation [Standard Forms]

1. Functional Form:

   An optimization problem is a problem of the form \(p^\ast := \displaystyle\min_x f_0(x) : f_i(x) \le 0, \ \ i=1,\ldots, m\),
   where:

   • \(x \in \mathbf{R}^n\) is the decision variable;

   • \(f_0 : \mathbf{R}^n \rightarrow \mathbf{R}\) is the objective function, or cost;

   • \(f_i : \mathbf{R}^n \rightarrow \mathbf{R}, \ \ i=1, \ldots, m\) represent the constraints;

   • \(p^\ast\) is the optimal value.

   • Example. Visit the Book

2. Epigraph form:

   TODO

3. Other Standard-Forms:

   TODO