


Linear Functions and Transformations, and Maps
-
- Linear Functions:
- Linear functions are functions which preserve scaling and addition of the input argument.
-
Formally,
- A function \(f: \mathbf{R}^n \rightarrow \mathbf{R}\) is linear if and only if \(f\) preserves scaling and addition of its arguments:
-
- for every \(x \in \mathbf{R}^n\), and \(\alpha \in \mathbf{R}, \ f(\alpha x) = \alpha f(x)\); and
-
- for every \(x_1, x_2 \in \mathbf{R}^n, f(x_1+x_2) = f(x_1)+f(x_2)\).
-
- Affine Functions:
- Affine functions are linear functions plus constant functions.
- Formally,
- A function f is affine if and only if the function \(\tilde{f}: \mathbf{R}^n \rightarrow \mathbf{R}\) with values \(\tilde{f}(x) = f(x)-f(0)\) is linear. \(\diamondsuit\)
-
Equivalently,
- A map \(f : \mathbf{R}^n \rightarrow \mathbf{R}^m\) is affine if and only if the map \(g : \mathbf{R}^n \rightarrow \mathbf{R}^m\) with values \(g(x) = f(x) - f(0)\) is linear.
-
- Quadratic Function
- A function \(q : \mathbf{R}^n \rightarrow \mathbf{R}\) is said to be a quadratic function if it can be expressed as
- \[q(x) = \sum_{i=1}^n \sum_{j=1}^n A_{ij} x_i x_j + 2 \sum_{i=1}^n b_i x_i + c,\]
- for numbers \(A_{ij}, b_i,\) and \(c, i, j \in {1, \ldots, n}\).
A quadratic function is thus an affine combination of the \(\ x_i\)’s and all the “cross-products” \(x_ix_j\).
-
We observe that the coefficient of \(x_ix_j\) is \((A_{ij} + A_{ji})\).
-
The function is said to be a quadratic form if there are no linear or constant terms in it: \(b_i = 0, c=0.\)
-
The Hessian of a quadratic function is always constant.
-
- Equivalent Definitions of Linear Functions [Theorem]:
- A map \(f : \mathbf{R}^n \rightarrow \mathbf{R}^m\) is linear if and only if either one of the following conditions hold:
-
- \(f\) preserves scaling and addition of its arguments:
- for every \(x \in \mathbf{R}^n\), and \(\alpha \in \mathbf{R}, f(\alpha x) = \alpha f(x)\); and
- for every \(x_1, x_2 \in \mathbf{R}^n, f(x_1+x_2) = f(x_1)+f(x_2).\)
- \(f\) preserves scaling and addition of its arguments:
-
- \(f\) vanishes at the origin:
- \(f(0) = 0\), and
- It transforms any line segment \(\in \mathbf{R}^n\) into another segment \(\in \mathbf{R}^m\):
\(\forall \: x, y \in \mathbf{R}^n, \; \forall \: \lambda \in [0,1] ~:~ f(\lambda x + (1-\lambda) y) = \lambda f(x) + (1-\lambda) f(y)\).
- \(f\) is differentiable, vanishes at the origin, and the matrix of its derivatives is constant.
- There exist \(A \in \mathbf{R}^{m \times n}\) such that, \(\ \forall x \in \mathbf{R}^n ~:~ f(x) = Ax\).
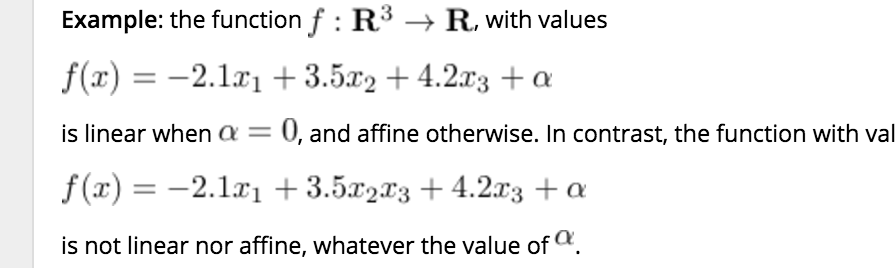
- \(f\) vanishes at the origin:
- Vector Form (and the scalar product):
Theorem: Representation of affine function via the scalar product.
\(\ \ \ \ \ \ \ \\) A function \(f: \mathbf{R}^n \rightarrow \mathbf{R}\) is affine if and only if it can be expressed via a scalar product:
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\) \(\ \ \ \ \ \ \ \ \ \\) \(f(x) = a^Tx + b\) ,
\(\ \ \ \ \ \ \ \\) for some unique pair \((a,b)\), with \(a \in \mathbf{R}^{n}\) and \(b \in \mathbf{R}\), given by \(a_i = f(e_i)-f(0)\), with \(e_i\) \(\ \ \ \ \ \ \ \ \\)the \(i-th\) unit vector \(\in \mathbf{R}^n, i=1, \ldots, n,\) and \(\ b = f(0)\).
The function is linear \(\iff b = 0\).
The theorem shows that a vector can be seen as a (linear) function from the “input” space \(\mathbf{R}^n\) to the “output” space \(\mathbf{R}\).
Both points of view (matrices as simple collections of numbers, or as linear functions) are useful.
-
Gradient of a Linear Function:

-
- Gradient of an Affine Function:
- The gradient of a function \(f : \mathbf{R}^n \rightarrow \mathbf{R}\) at a point \(x\), denoted \(\nabla f(x)\), is the vector of first derivatives with respect to \(x_1, \ldots, x_n\).
-
When \(n=1\) (there is only one input variable), the gradient is simply the derivative.
- An affine function \(f : \mathbf{R}^n \rightarrow \mathbf{R}\), with values \(f(x) = a^Tx+b\) has the gradient:
- \(\nabla f(x) = a\).
-
i.e. For all Affine Functions, the gradient is the constant vector \(a\).
-
- Interpreting \(a\) and \(b\):
-
- The \(b=f(0)\) is the constant term. For this reason, it is sometimes referred to as the bias, or intercept.
as it is the point where \(f\) intercepts the vertical axis if we were to plot the graph of the function.
- The \(b=f(0)\) is the constant term. For this reason, it is sometimes referred to as the bias, or intercept.
-
- The terms \(a_j, j=1, \ldots, n,\) which correspond to the gradient of \(f\), give the coefficients of influence of \(x_j\) on \(f\).
For example, if \(a_1 >> a_3\), then the first component of \(x\) has much greater influence on the value of \(f(x)\) than the third.
- The terms \(a_j, j=1, \ldots, n,\) which correspond to the gradient of \(f\), give the coefficients of influence of \(x_j\) on \(f\).
-
- First-order approximation of non-linear functions:
-
- One-dimensional case:
Consider a function of one variable \(f : \mathbf{R} \rightarrow \mathbf{R}\), and assume it is differentiable everywhere.
Then we can approximate the values function at a point \(x\) near a point \(x_0\) as follows:
- One-dimensional case:
- \[f(x) \simeq l(x) := f(x_0) + f'(x_0) (x-x_0) ,\]
- \(\ \ \ \ \ \ \ \\) where \(f'(x)\) denotes the derivative of \(f\) at \(x\).
-
- Multi-dimensional:
Let us approximate a differentiable function \(f : \mathbf{R}^n \rightarrow \mathbf{R}\) by a linear function \(l\), so that \(f\) and \(l\) coincide up and including to the first derivatives.
The approximate function l must be of the form:
- Multi-dimensional:
- \[l(x) = a^Tx + b,\]
- \(\ \ \ \ \ \ \ \\) where \(a \in \mathbf{R}^n\) and \(b \in \mathbf{R}\).
-
The corresponding approximation \(l\) is called the first-order approximation to \(f\) at \(x_0\).
-
- Our condition that \(l\) coincides with \(f\) up and including to the first derivatives shows that we must have:
- \[\nabla l(x) = a = \nabla f(x_0), \;\; a^Tx_0 + b = f(x_0),\]
- \(\ \ \ \ \ \ \ \\) where \(\nabla f(x_0)\) is the gradient, of \(f\) at \(x_0\).
-
- First-order Expansion of a function [Theorem]:
- The first-order approximation of a differentiable function \(f\) at a point \(x_0\) is of the form:
- \[f(x) \approx l(x) = f(x_0) + \nabla f(x_0)^T (x-x_0)\]
- where \(\nabla f(x_0) \in \mathbf{R}^n\) is the gradient of \(f\) at \(x_0\).


Matrices
-
- Matrix Transpose:
- \[A_{ij} = A_{ji}^T, \; \forall i, j \in \mathbf{F}\]
- Properties:
- \[(AB)^T = B^TA^T.\]
-
- Matrix-vector product:
- \[(Ax)_i = \sum_{j=1}^n A_{ij}x_j , \;\; i=1, \ldots, m.\]
- Where the Matrix is \(\in {\mathbf{R}}^{m \times n}\) and the vector is \(\in {\mathbf{R}}^m\).
- Interpretations:
-
-
A linear combination of the columns of \(A\):
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Ax = \left( \begin{array}{c} a_1^Tx \ldots a_m^Tx \end{array} \right)^T\) .
where the columns of \(A\) are given by the vectors \(a_i, i=1, \ldots, n\), so that \(A = (a_1 , \ldots, a_n)\). -
Scalar Products of Rows of \(A\) with \(x\):
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Ax = \sum_{i=1}^n x_i a_i\) .
where the rows of \(A\) are given by the vectors \(a_i^T, i=1, \ldots, m\): \(A = \left( \begin{array}{c} a_1^T \ldots a_m^T \end{array} \right)^T\).
-

-
- Left Product:
- If \(z \in \mathbf{R}^m\), then the notation \(z^TA\) is the row vector of size \(n\) equal to the transpose of the column vector \(A^Tz \in \mathbf{R}^n\):
- \((z^TA)_j = \sum_{i=1}^m A_{ij}z_i , \;\; j=1, \ldots, n.\)
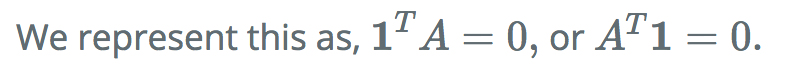
-
- Matrix-matrix product:
- \((AB)_{ij} = \sum_{k=1}^n A_{ik} B_{kj}\).
- where \(A \in \mathbf{R}^{m \times n}\) and \(B \in \mathbf{R}^{n \times p}\), and the notation \(AB\) denotes the \(m \times p\) matrix given above.
- Interpretations:
-
- Transforming the columns of \(B\) into \(Ab_i\):
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ AB = A \left( \begin{array}{ccc} b_1 & \ldots & b_n \end{array} \right) = \left( \begin{array}{ccc} Ab_1 & \ldots & Ab_n \end{array} \right)\) .
where the columns of \(B\) are given by the vectors \(b_i, i=1, \ldots, n\), so that \(B = (b_1 , \ldots, b_n)\). - Transforming the Rows of \(A\) into \(a_i^TB\):
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ AB = \left(\begin{array}{c} a_1^T \\ \vdots \\ a_m^T \end{array}\right) B = \left(\begin{array}{c} a_1^TB \\ \vdots \\ a_m^TB \end{array}\right)\).
where the rows of \(A\) are given by the vectors \(a_i^T, i=1, \ldots, m\): \(A = \left( \begin{array}{c} a_1^T \ldots a_m^T \end{array} \right)^T\).
- Transforming the columns of \(B\) into \(Ab_i\):
-
Block Matrix Products:

-
Outer Products:

-
- Trace:
- The trace of a square \(n \times n\) matrix \(A\), denoted by \(\mathbf{Tr} A\), is the sum of its diagonal elements:
- \(\mathbf{Tr} A = \sum_{i=1}^n A_{ii}\).
- Properties:
- \(\mathbf{Tr} A = \mathbf{Tr} A^T\).
- \(\mathbf{Tr} (AB) = \mathbf{Tr} (BA)\).
- \(\mathbf{Tr}(XYZ) = \mathbf{Tr}(ZXY) = \mathbf{Tr}(YZX)\).
- \({\displaystyle \operatorname{tr} (A+B) = \operatorname{tr} (A)+\operatorname{tr} (B)}\).
- \({\displaystyle \operatorname{tr} (cA) = c\operatorname{tr} (A)}\).
- \({\displaystyle \operatorname{tr} \left(X^{\mathrm {T} }Y\right)=\operatorname{tr} \left(XY^{\mathrm {T} }\right)=\operatorname{tr} \left(Y^{\mathrm {T} }X\right)=\operatorname{tr} \left(YX^{\mathrm {T} }\right)=\sum _{i,j}X_{ij}Y_{ij}}\).
- \({\displaystyle \operatorname{tr} \left(X^{\mathrm {T} }Y\right)=\sum _{ij}(X\circ Y)_{ij}}\ \ \ \\) (The Hadamard product).
- Arbitrary permutations of the product of matrices is not allowed. Only, cyclic permutations are.
However, if products of three symmetric matrices are considered, any permutation is allowed.
- The trace of an idempotent matrix \(A\), is the dimension of A.
- The trace of a nilpotent matrix is zero.
- If \(f(x) = (x − \lambda_1)^{d_1} \cdots (x − \lambda_k)^{d_k}\) is the characteristic polynomial of a matrix \(A\), then \({\displaystyle \operatorname{tr} (A)=d_{1}\lambda_{1} + \cdots + d_{k} \lambda_{k}}\).
- When both \(A\) and \(B\) are \(n \times n\), the trace of the (ring-theoretic) commutator of \(A\) and \(B\) vanishes: \(\mathbf{tr}([A, B]) = 0\); one can state this as “the trace is a map of Lie algebras \({\displaystyle \mathbf{GL_{n}} \to k}\) from operators to scalars”, as the commutator of scalars is trivial (it is an abelian Lie algebra).
- The trace of a projection matrix is the dimension of the target space. \({\displaystyle P_{X} = X\left(X^{\mathrm {T} }X\right)^{-1}X^{\mathrm {T} } \\ \Rightarrow \\ \operatorname {tr} \left(P_{X}\right) = \operatorname {rank} \left(X\right)}\)
-
- Scalar Product:
- \[\langle A, B \rangle := \mathbf{Tr}(A^TB) = \displaystyle\sum_{i=1}^m\sum_{j=1}^n A_{ij}B_{ij}.\]
-
The above definition is Symmetric:
- \[\implies \langle A,B \rangle = \mathbf{Tr} (A^TB) = \mathbf{Tr} (A^TB)^T = \mathbf{Tr} (B^TA) = \langle B,A \rangle .\]
-
We can interpret the matrix scalar product as the vector scalar product between two long vectors of length \(mn\) each, obtained by stacking all the columns of \(A, B\) on top of each other.
- Special Matrices:
- Diagonal matrices: are square matrices \(A\) with \(A_{ij} = 0\) when \(i \ne j\).
- Symmetric matrices: are square matrices that satisfy \(A_{ij} = A_{ji}\)for every pair \((i,j)\).
-
Triangular matrices: are square matrices that satisfy \(A_{ij} = A_{ji}\)for every pair \((i,j)\).
{F}}^{2}=|AR|{\rm {F}}^{2}=|RA|{\rm {F}}^{2}}\(for any rotation matrix\)R$$.-
Invariant under a unitary transformation for complex matrices.
-
\({\displaystyle \|A^{\rm {T}}A\|_{\rm {F}}=\|AA^{\rm {T}}\|_{\rm {F}}\leq \|A\|_{\rm {F}}^{2}}\).
-
\({\displaystyle \|A+B\|_{\rm {F}}^{2}=\|A\|_{\rm {F}}^{2}+\|B\|_{\rm {F}}^{2}+2\langle A,B\rangle _{\mathrm {F} }}\).
-
-
- \(l_{\infty,\infty}\) (Max Norm):
- \[\|A\|_{\max} = \max_{ij} |a_{ij}|.\]
- Properties:
- NOT Submultiplicative.
-
- The Spectral Norm:
- \({\displaystyle \|A\|_{2}={\sqrt {\lambda _{\max }(A^{^{*}}A)}}=\sigma _{\max }(A)} = {\displaystyle \max_{\|x\|_2!=0}(\|Ax\|_2)/(\|x\|_2)}.\)
The spectral norm of a matrix \({\displaystyle A}\) is the largest singular value of \({\displaystyle A}\). i.e. the square root of the largest eigenvalue of the positive-semidefinite matrix \({\displaystyle A^{*}A}.\)
-
- The Spectral Radius of \(A \\) [denoted \(\rho(A)\)]:
- \[\lim_{r\rightarrow\infty}\|A^r\|^{1/r}=\rho(A).\]
- Properties:
-
Submultiplicative.
-
Satisfies, \({\displaystyle \|A^{r}\|^{1/r}\geq \rho (A),}\), where \(\rho(A)\) is the spectral radius of \(A\).
-
It is an “induced vector-norm”.
-
-
Asynchronous:
-
Asynchronous:
-
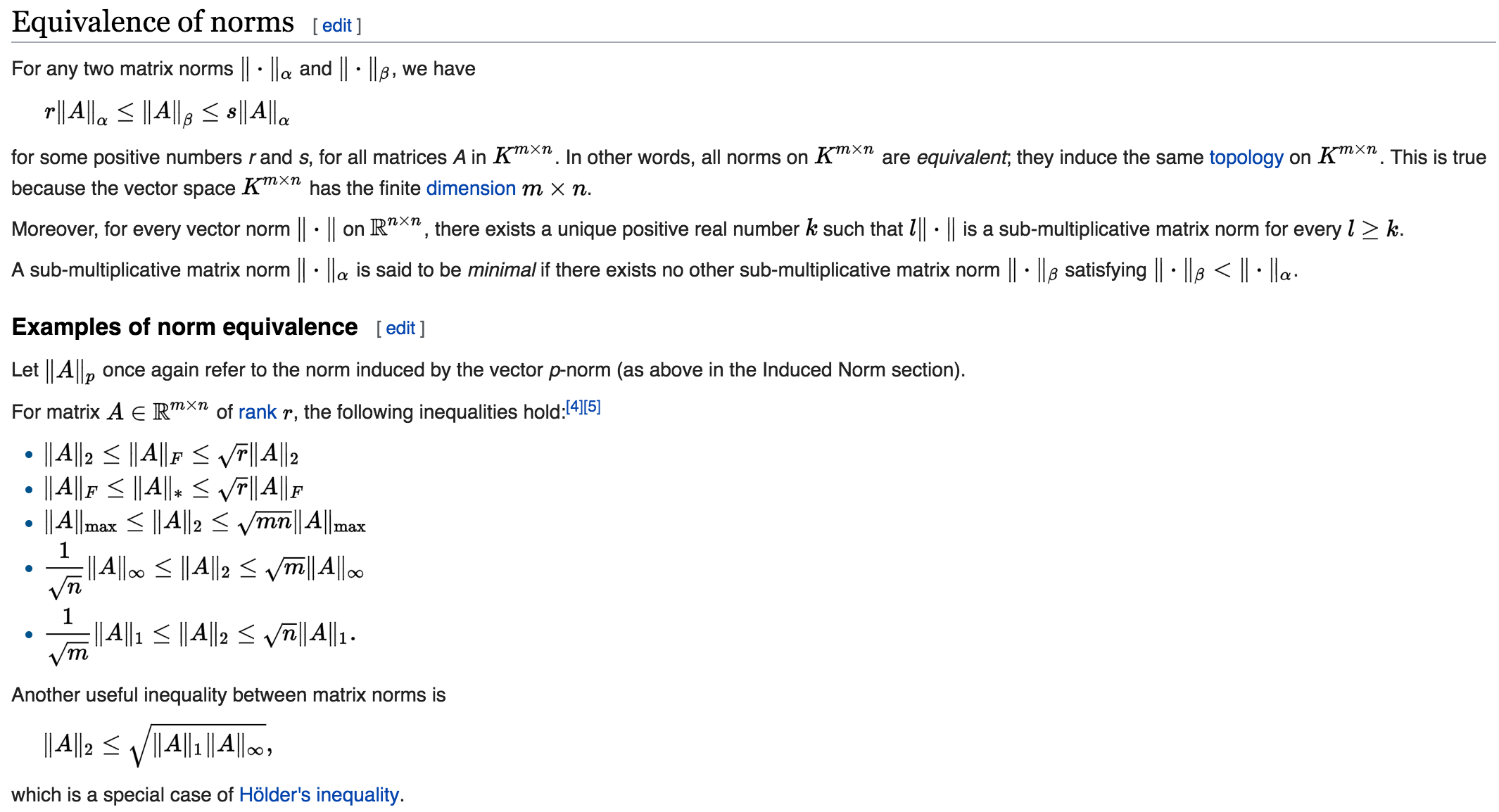
Equivalence of Norms:
- Applications:
-
RMS Gain: Frobenius Norm.
-
Peak Gain: Spectral Norm.
-
Distance between Matrices: Frobenius Norm.

-
Direction of Maximal Variance: Spectral Norm.

-