Table of Contents
Definitions
-
- Linear Independence:
- A set of vectors \(\{x_1, ... , x_m\} \in {\mathbf{R}}^n, i=1, \ldots, m\) is said to be independent if and only if the following condition on a vector \(\lambda \in {\mathbf{R}}^m\):
-
\[\sum_{i=1}^m \lambda_i x_i = 0 \ \ \ \implies \lambda = 0.\]
i.e. no vector in the set can be expressed as a linear combination of the others.
-
- Subspace:
- A subspace of \({\mathbf{R}}^n\) is a subset that is closed under addition and scalar multiplication. Geometrically, subspaces are “flat” (like a line or plane in 3D) and pass through the origin.
- A Subspace \(\mathbf{S}\) can always be represented as the span of a set of vectors \(x_i \in {\mathbf{R}}^n, i=1, \ldots, m\), that is, as a set of the form:
\(\mathbf{S} = \mbox{ span}(x_1, \ldots, x_m) := \left\{ \sum_{i=1}^m \lambda_i x_i ~:~ \lambda \in {\mathbf{R}}^m \right\}.\)
-
- Affine Sets (Cosets | Abstract Algebra):
- An affine set is a translation of a subspace — it is “flat” but does not necessarily pass through 0, as a subspace would.
(Think for example of a line, or a plane, that does not go through the origin.)
- An affine set \(\mathbf{A}\) can always be represented as the translation of the subspace spanned by some vectors:
- \(\mathbf{A} = \left\{ x_0 + \sum_{i=1}^m \lambda_i x_i ~:~ \lambda \in {\mathbf{R}}^m \right\}\ \ \\), for some vectors \(x_0, x_1, \ldots, x_m.\)
-
(Special case) lines: When \(\mathbf{S}\) is the span of a single non-zero vector, the set \(\mathbf{A}\) is called a line passing through the point \(x_0\). Thus, lines have the form \(\left\{ x_0 + tu ~:~ t \in \mathbf{R} \right\}\),
where \(u\) determines the direction of the line, and \(x_0\) is a point through which it passes. -

-
- Basis:
- A basis of \({\mathbf{R}}^n\) is a set of \(n\) independent vectors. If the vectors \(u_1, \ldots, u_n\) form a basis, we can express any vector as a linear combination of the \(u_i\)’s:
- \(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x = \sum_{i=1}^n \lambda_i u_i, \ \ \ \text{for appropriate numbers } \lambda_1, \ldots, \lambda_n\).
-
- Dimension:
- The number of vectors in the span of the (sub-)space.
Norms and Scalar Products
-
- Scalar Product:
- The scalar product (or, inner product, or dot product) between two vectors \(x,y \in \mathbf{R}^n\) is the scalar denoted \(x^Ty\), and defined as:
- \[x^Ty = \sum_{i=1}^n x_i y_i.\]
-
- Norms:
- A measure of the “length” of a vector in a given space.
- Theorem. A function from \(\chi\) to \(\mathbf{R}\) is a norm, if:
- \(\|x\| \geq 0, \: \forall x \in \chi\), and \(\|x\| = 0 \iff x = 0\).
- \(\|x+y\| \leq \|x\| + \|y\|,\) for any \(x, y \in \chi\) (triangle inequality).
- \(\|\alpha x\| = \|\alpha\| \|x\|\), for any scalar \(\alpha\) and any \(x\in \chi\).
-
\(l_p\) Norms: \(\|x\|_p = \left( \sum_{k=1}^n \|x_k\|^p \right)^{1/p}, \ 1 \leq p < \infty\)
-
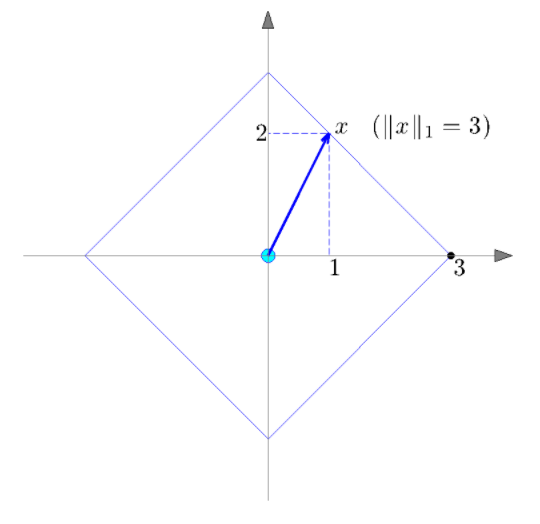
- The \(l_1-norm\):
- \[\|x\|_1 := \sum_{i=1}^n \| x_i \|\]
- Corresponds to the distance travelled on a rectangular grid to go from one point to another.
-
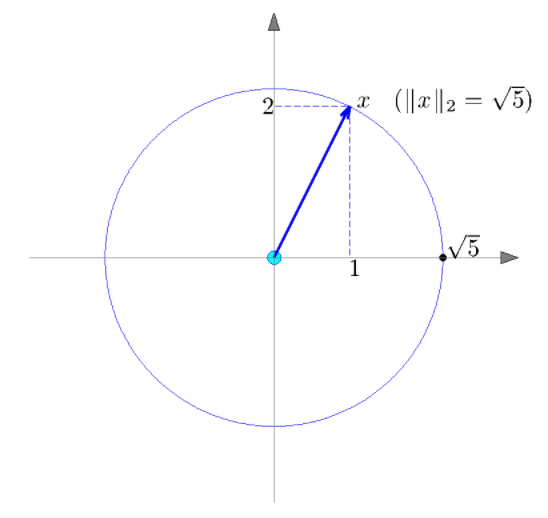
- The \(l_2-norm\) (Euclidean Norm):
- \(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \| x \|_2 := \sqrt{ \sum_{i=1}^n x_i^2 } = \sqrt{x^Tx}\).
- Corresponds to the usual notion of distance in two or three dimensions.
-
The \(l_2-norm\) is invariant under orthogonal transformations,
i.e., \(\|x\|_2 = \|Vz\|_2 = \|z\|_2,\) where \(V\) is an orthogonal matrix. -
The set of points with equal l_2-norm is a circle (in 2D), a sphere (in 3D), or a hyper-sphere in higher dimensions.
-
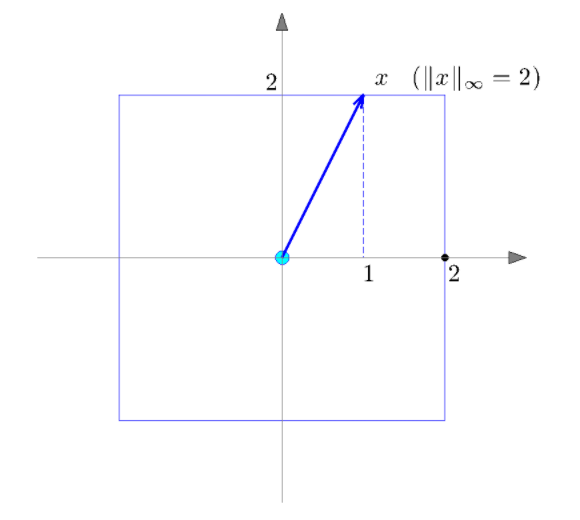
- The \(l_\infty-norm\):
- \[\| x \|_\infty := \displaystyle\max_{1 \le i \le n} \| x_i \|\]
-
useful in measuring peak values.
-
- The Cardinality:
- The Cardinality of a vector \(\vec{x}\) is often called the \(l_0\) (pseudo) norm and denoted with,
- \(\|\vec{x}\|_0\).
-
Defined as the number of non-zero entries in the vector.
-
- Cauchy-Schwartz inequality:
- For any two vectors \(x, y \in \mathbf{R}^n\), we have
- \(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\) \(\ \ \ \ \ \ \ \ \ \ \ \ \\) \(x^Ty \le \|x\|_2 \cdot \|y\|_2\).
- The above inequality is an equality if and only if \(x, y\) are collinear:
- \({\displaystyle \max_{x : \: \|x\|_2 \le 1} \: x^Ty = \|y\|_2,}\)
with optimal \(x\) given by
\(x^\ast = \dfrac{y}{\|y\|_ 2}, \\) if \(y\) is non-zero.
-
- Angles between vectors:
- When none of the vectors x,y is zero, we can define the corresponding angle as theta such that,
- \[\cos\ \theta = \dfrac{x^Ty}{\|x\|_ 2 \|y\|_ 2} .\]
Notes:
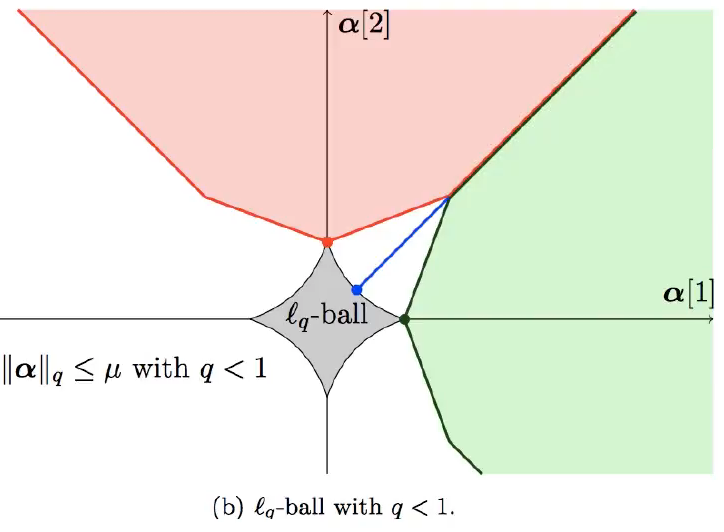
- \(L^q\) for \(q \in (0,1)\) are no longer Norms.
- They have non-convex contours; thus, using them makes the optimization much harder
- They, however, induce more sparsity than \(L^1\)
- \(L^1\) is the best, sparse norm, convex approximation to the \(L^q\) for \(q \in (0,1)\)
Orthogonality
-
- Orthogonal Vectors:
- We say that two vectors \(x, y \in \mathbf{R}^n\) are orthogonal if \(x^Ty = 0.\)
Projections
-
- Line:
- A line in \(\mathbf{R}^n\) passing through \(x_0 \in \mathbf{R}^n\) and with direction \(u \in \mathbf{R}^n\):
- \(\left\{ x_0 + tu ~:~ t \in \mathbf{R} \right\}\),
Re-Written:
A line in \(\mathbf{R}^n\) passing through the point \(x_0 \in \mathbf{R}^n\) and with direction \(\mathbf{u} \in \mathbb{R}^n\):$$\left\{ x_0 + c \mathbf{u} ~:~ c \in \mathbb{R} \right\}$$
-
- Projection on a line:
- The projection of a given point \(\vec{x}\) on the line is a vector \(\vec{z}\) located on the line, that is closest to \(\vec{x}\) (in Euclidean norm). This corresponds to a simple optimization problem:
- \(\min_t \: \|x - x_0 - tu\|_ 2^2\).
-
This particular problem is part of a general class of optimization problems known as least-squares.
-
It is also a special case of a Euclidean projection on a general set.
Re-Written:
The projection of a given point \(\mathbf{v}\) on the line is a vector \(\tilde{\mathbf{v}}\) located on the line, that is closest (distance-wise) to \(\mathbf{v}\) (in Euclidean norm). This corresponds to a simple optimization problem:$$\min_c \: \|\mathbf{v} - x_0 - c \mathbf{u}\|_ 2^2$$
-
- The Projection:
- Assuming that \(\vec{u}\) is normalized, so that \(\|\vec{u}\|_2 = 1\), the objecive function of the projection problem reads, after squaring:
- \[\|x - x_0 - tu\|_2^2 = t^2 - 2t u^T(x-x_0) + \|x-x_0\|_2^2 = (t - u^T(x-x_0))^2 + \mbox{constant}.\]
- \(\implies \\\) [the optimal solution to the projection problem is]
- \[t^\ast = u^T(x-x_0),\]
- and the expression for the projected vector is
- \[z^\ast = x_0 + t^\ast u = x_0 + u^T(x-x_0) u.\]
-
The scalar product \(u^T(x-x_0)\) is the component of \(x-x_0\) along \(\vec{u}\).
-
In the case when u is not normalized, the expression is obtained by replacing \(\vec{u}\) with its scaled version \(\dfrac{\vec{u}}{\|\vec{u}\|_2}\).
- The General Solution:
- \[\vec{z}^\ast = \vec{x_0} + \dfrac{\vec{u}^T(\vec{x}-\vec{x_0})}{\vec{u}^T\vec{u}} \vec{u} .\]
-
- Interpreting the scalar product:
- In general, the scalar product, \(u^Tx\), is simply,
the component of \(x\) along the normalized direction \(\dfrac{\vec{u}}{\|\vec{u}\|_2}\) defined by \(\vec{u}\).
- Projection:
A Projection is a linear transformation \(P\) from a vector-space to itself such that the matrix \(P\) is idempotent:$$P^2 = P$$
It leaves its image unchanged.
Mathematically:
A Projection on a vector space \({\displaystyle V}\) is a linear operator \({\displaystyle P:V\mapsto V}\) such that \({\displaystyle P^{2}=P}\)Properties:
- The Eigenvalues of a projection matrix must be \(0\) or \(1\)
From the equation \(P^2 = P \iff x^2 = x = x(x-1)\) has roots \(0, 1\)
- \({\displaystyle P}\) is always a positive semi-definite matrix
Follows from the fact that the eigenvalues are either \(0\) or \(1\)
- The corresponding eigenspaces are (respectively) the kernel and range of the projection
- If a projection is nontrivial it has minimal polynomial \({\displaystyle x^{2}-x=x(x-1)}\), which factors into distinct roots, and thus \({\displaystyle P}\) is diagonalizable
- The product of projections is not, in general, a projection, even if they are orthogonal.
- If projections commute, then their product is a projection.
Notes:
- The Centering Matrix: is an example of a projection matrix
- The Eigenvalues of a projection matrix must be \(0\) or \(1\)
- Orthogonal Projections:
An Orthogonal Projection is a projection \(P\) from a vector-space to itself such that the matrix \(P\) is symmetric:$$P = P^T$$
Mathematically:
- When \({\displaystyle V}\) has an inner product and is complete (i.e. when \({\displaystyle V}\) is a Hilbert space) the concept of orthogonality can be used.
Then \({\displaystyle P}\) is called an orthogonal projection if it satisfies \({\displaystyle \langle Px,y\rangle =\langle x,Py\rangle }\) for all \({\displaystyle x,y\in V}\) - A projection on a Hilbert space that is not orthogonal is called an oblique projection.
- A square matrix \({\displaystyle P}\) is called an orthogonal projection matrix if \({\displaystyle P^{2}=P=P^{\mathrm {T} }}\)
- The range \({\displaystyle U}\) and the null space \({\displaystyle V}\) are orthogonal subspaces:
$$\langle x,Py\rangle =\langle Px,Py\rangle =\langle Px,y\rangle$$
- An orthogonal projection is a bounded operator.
By Cauchy Schwartz:$${\displaystyle \|Pv\|^{2}=\langle Pv,Pv\rangle =\langle Pv,v\rangle \leq \|Pv\|\cdot \|v\|} \\ \iff \\ {\displaystyle \|Pv\|\leq \|v\|}$$
Orthogonal Projection onto a Line:
If \(\hat{u}\) is a unit vector on the line, then the projection is given by the outer-product:$$P_{\hat{u}} = \hat{u}\hat{u}^T$$
Orthogonal Projection onto Subspaces:
Generalize the above definition, if \({\displaystyle \hat{u}_{1},\ldots ,\hat{u}_{k}}\) are an orthonormal basis of the subspace \(U\), and \(A\) is the \(n \times k\) matrix with columns \({\displaystyle \hat{u}_{1},\ldots ,\hat{u}_{k}}\), then the projection is given by:$$P_A = AA^T$$
Equivalently:
$$P_{A}=\sum _{i}\langle u_{i},\cdot \rangle u_{i}$$
Dropping the Orthonormality condition on the basis, we get:
$$P_{A}=A(A^{\mathrm {T} }A)^{-1}A^{\mathrm {T} }$$
- When \({\displaystyle V}\) has an inner product and is complete (i.e. when \({\displaystyle V}\) is a Hilbert space) the concept of orthogonality can be used.
Hyperplanes
-
- Hyperplanes:
- A hyperplane is a set described by a single scalar product equality. Precisely, a hyperplane \(\in \mathbf{R}^n\) is a set of the form:
- \[\mathbf{H} = \left\{ x ~:~ a^Tx = b \right\},\]
- where a \(\in \mathbf{R}^n, a \ne 0\), and \(b \in \mathbf{R}\) are given.
-
When \(b=0\), the hyperplane is simply the set of points that are orthogonal to \(a\).
-
when \(b \ne 0\), the hyperplane is a translation, along direction \(a\), of that set.
-
If \(x_0 \in \mathbf{H}\), then for any other element \(x \in \mathbf{H}\), we have
- \[b = a^Tx_0 = a^Tx.\]
- Hence, the hyperplane can be characterized as the set of vectors \(x\) such that \(x-x_0\) is orthogonal to \(a\):
- \(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{H} = \left\{ x ~:~ a^T(x-x_0)=0 \right\}\).
-
- Hyper-Planes as Affine Sets:
- Hyper-planes are affine sets of degree \(n-1\).

-
Thus, they generalize the usual notion of a plane \(\in \mathbf{R}^3\).
-
Hyperplanes are very useful because they allows to separate the whole space in two regions.
-
- Geometry of Hyperplanes:
- Geometrically, an hyperplane \(\mathbf{H} = \left\{ x ~:~ a^Tx = b \right\}\), with \(\|a\|_2 = 1\), is a:
-
- Translation of the set of vectors orthogonal to a.
-
- The Direction of the translation is determined by a, and the amount by b.
-
- \(abs(b)\) is, Precisely, the length of the closest point \(x_0\) on \(\mathbf{H}\) from the origin.
-
- The sign of \(b\) determines if \(\mathbf{H}\) is away from the origin along the direction \(a\) or \(-a\).
-
- The magnitude of \(b\), determines the shifting of the hyperplane, as follows:
- Increasing the magnitude: shifts the hyperplane further away along \(\pm a\), depending on the sign of \(b\).
- Decreasing the magnitude: shifts the hyperplane closer along \(\pm a\), depending on the sign of \(b\).
- The magnitude of \(b\), determines the shifting of the hyperplane, as follows:
-
In the image below, the scalar b is positive, as \(x_0\) and a point to the same direction.
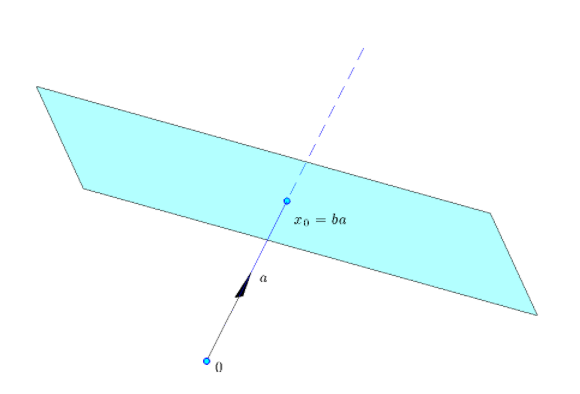
Half-Spaces
-
- Half-Space:
- A half-space is a subset of \(\mathbf{R}^n\) defined by a single inequality involving a scalar product. Precisely, a half-space \(\in \mathbf{R}^n\) is a set of the form:
- \[\mathbf{H} = \left\{ x ~:~ a^Tx \ge b \right\},\]
- where \(a \in \mathbf{R}^n, a \ne 0,\) and \(b \in \mathbf{R}\) are given.
-
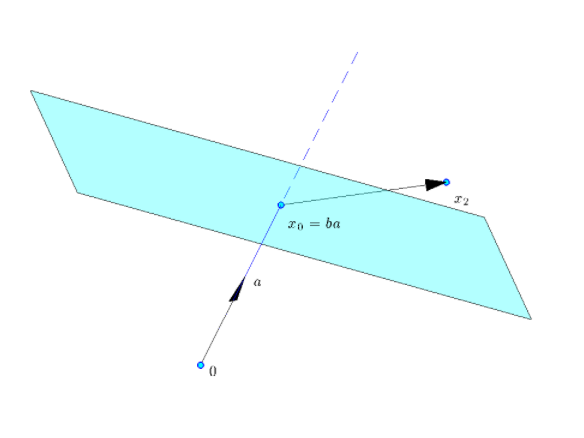
- Geometric Interptation:
- Geometrically, the half-space above is:
-
- The set of points such that \(a^T(x-x_0) \ge 0\).
-
i.e. The angle between \(x-x_0\) and \(a\) is acute \((\in [-90^\circ, +90^\circ])\).
-
- \(x_0\): is the point closest to the origin on the hyperplane defined by the equality \(a^Tx = b\).
-
When \(a\) is normalized, as in the picture, \(x_0 = ba\).
Linear Functions and Transformations, and Maps
-
- Linear Functions:
- Linear functions are functions which preserve scaling and addition of the input argument.
-
Formally,
- A function \(f: \mathbf{R}^n \rightarrow \mathbf{R}\) is linear if and only if \(f\) preserves scaling and addition of its arguments:
-
- for every \(x \in \mathbf{R}^n\), and \(\alpha \in \mathbf{R}, \ f(\alpha x) = \alpha f(x)\); and
-
- for every \(x_1, x_2 \in \mathbf{R}^n, f(x_1+x_2) = f(x_1)+f(x_2)\).
-
- Affine Functions:
- Affine functions are linear functions plus constant functions.
- Formally,
- A function f is affine if and only if the function \(\tilde{f}: \mathbf{R}^n \rightarrow \mathbf{R}\) with values \(\tilde{f}(x) = f(x)-f(0)\) is linear. \(\diamondsuit\)
-
Equivalently,
- A map \(f : \mathbf{R}^n \rightarrow \mathbf{R}^m\) is affine if and only if the map \(g : \mathbf{R}^n \rightarrow \mathbf{R}^m\) with values \(g(x) = f(x) - f(0)\) is linear.
-
- Equivalent Definitions of Linear Functions [Theorem]:
- A map \(f : \mathbf{R}^n \rightarrow \mathbf{R}^m\) is linear if and only if either one of the following conditions hold:
-
- \(f\) preserves scaling and addition of its arguments:
- for every \(x \in \mathbf{R}^n\), and \(\alpha \in \mathbf{R}, f(\alpha x) = \alpha f(x)\); and
- for every \(x_1, x_2 \in \mathbf{R}^n, f(x_1+x_2) = f(x_1)+f(x_2).\)
- \(f\) preserves scaling and addition of its arguments:
-
- \(f\) vanishes at the origin:
- \(f(0) = 0\), and
- It transforms any line segment \(\in \mathbf{R}^n\) into another segment \(\in \mathbf{R}^m\):
\(\forall \: x, y \in \mathbf{R}^n, \; \forall \: \lambda \in [0,1] ~:~ f(\lambda x + (1-\lambda) y) = \lambda f(x) + (1-\lambda) f(y)\).
- \(f\) is differentiable, vanishes at the origin, and the matrix of its derivatives is constant.
- There exist \(A \in \mathbf{R}^{m \times n}\) such that, \(\ \forall x \in \mathbf{R}^n ~:~ f(x) = Ax\).
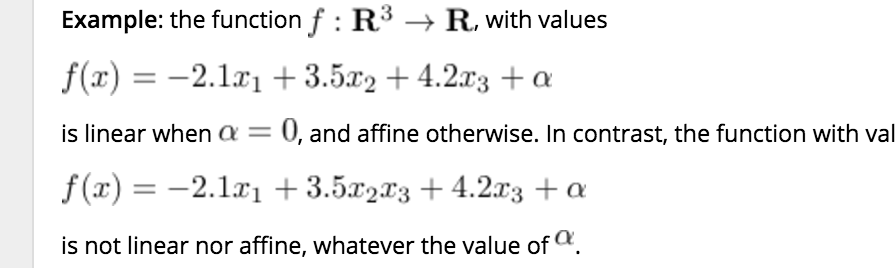
- \(f\) vanishes at the origin:
- Vector Form (and the scalar product):
Theorem: Representation of affine function via the scalar product.
\(\ \ \ \ \ \ \ \\) A function \(f: \mathbf{R}^n \rightarrow \mathbf{R}\) is affine if and only if it can be expressed via a scalar product:
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\) \(\ \ \ \ \ \ \ \ \ \\) \(f(x) = a^Tx + b\) ,
\(\ \ \ \ \ \ \ \\) for some unique pair \((a,b)\), with \(a \in \mathbf{R}^{n}\) and \(b \in \mathbf{R}\), given by \(a_i = f(e_i)-f(0)\), with \(e_i\) \(\ \ \ \ \ \ \ \ \\)the \(i-th\) unit vector \(\in \mathbf{R}^n, i=1, \ldots, n,\) and \(\ b = f(0)\).
The function is linear \(\iff b = 0\).
The theorem shows that a vector can be seen as a (linear) function from the “input” space \(\mathbf{R}^n\) to the “output” space \(\mathbf{R}\).
Both points of view (matrices as simple collections of numbers, or as linear functions) are useful.
-
Gradient of a Linear Function:

-
- Gradient of an Affine Function:
- The gradient of a function \(f : \mathbf{R}^n \rightarrow \mathbf{R}\) at a point \(x\), denoted \(\nabla f(x)\), is the vector of first derivatives with respect to \(x_1, \ldots, x_n\).
-
When \(n=1\) (there is only one input variable), the gradient is simply the derivative.
- An affine function \(f : \mathbf{R}^n \rightarrow \mathbf{R}\), with values \(f(x) = a^Tx+b\) has the gradient:
- \(\nabla f(x) = a\).
-
i.e. For all Affine Functions, the gradient is the constant vector \(a\).
-
- Interpreting \(a\) and \(b\):
-
- The \(b=f(0)\) is the constant term. For this reason, it is sometimes referred to as the bias, or intercept.
as it is the point where \(f\) intercepts the vertical axis if we were to plot the graph of the function.
- The \(b=f(0)\) is the constant term. For this reason, it is sometimes referred to as the bias, or intercept.
-
- The terms \(a_j, j=1, \ldots, n,\) which correspond to the gradient of \(f\), give the coefficients of influence of \(x_j\) on \(f\).
For example, if \(a_1 >> a_3\), then the first component of \(x\) has much greater influence on the value of \(f(x)\) than the third.
- The terms \(a_j, j=1, \ldots, n,\) which correspond to the gradient of \(f\), give the coefficients of influence of \(x_j\) on \(f\).
-
- First-order approximation of non-linear functions:
-
- One-dimensional case:
Consider a function of one variable \(f : \mathbf{R} \rightarrow \mathbf{R}\), and assume it is differentiable everywhere.
Then we can approximate the values function at a point \(x\) near a point \(x_0\) as follows:
- One-dimensional case:
- \[f(x) \simeq l(x) := f(x_0) + f'(x_0) (x-x_0) ,\]
- \(\ \ \ \ \ \ \ \\) where \(f'(x)\) denotes the derivative of \(f\) at \(x\).
-
- Multi-dimensional:
Let us approximate a differentiable function \(f : \mathbf{R}^n \rightarrow \mathbf{R}\) by a linear function \(l\), so that \(f\) and \(l\) coincide up and including to the first derivatives.
The approximate function l must be of the form:
- Multi-dimensional:
- \[l(x) = a^Tx + b,\]
- \(\ \ \ \ \ \ \ \\) where \(a \in \mathbf{R}^n\) and \(b \in \mathbf{R}\).
-
The corresponding approximation \(l\) is called the first-order approximation to \(f\) at \(x_0\).
-
- Our condition that \(l\) coincides with \(f\) up and including to the first derivatives shows that we must have:
- \[\nabla l(x) = a = \nabla f(x_0), \;\; a^Tx_0 + b = f(x_0),\]
- \(\ \ \ \ \ \ \ \\) where \(\nabla f(x_0)\) is the gradient, of \(f\) at \(x_0\).
-
- First-order Expansion of a function [Theorem]:
- The first-order approximation of a differentiable function \(f\) at a point \(x_0\) is of the form:
- \[f(x) \approx l(x) = f(x_0) + \nabla f(x_0)^T (x-x_0)\]
- where \(\nabla f(x_0) \in \mathbf{R}^n\) is the gradient of \(f\) at \(x_0\).

Matrices
-
- Matrix Transpose:
- \[A_{ij} = A_{ji}^T, \; \forall i, j \in \mathbf{F}\]
- Properties:
- \[(AB)^T = B^TA^T.\]
-
- Matrix-vector product:
- \[(Ax)_i = \sum_{j=1}^n A_{ij}x_j , \;\; i=1, \ldots, m.\]
- Where the Matrix is \(\in {\mathbf{R}}^{m \times n}\) and the vector is \(\in {\mathbf{R}}^m\).
- Interpretations:
-
-
A linear combination of the columns of \(A\):
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Ax = \left( \begin{array}{c} a_1^Tx \ldots a_m^Tx \end{array} \right)^T\) .
where the columns of \(A\) are given by the vectors \(a_i, i=1, \ldots, n\), so that \(A = (a_1 , \ldots, a_n)\). -
Scalar Products of Rows of \(A\) with \(x\):
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Ax = \sum_{i=1}^n x_i a_i\) .
where the rows of \(A\) are given by the vectors \(a_i^T, i=1, \ldots, m\): \(A = \left( \begin{array}{c} a_1^T \ldots a_m^T \end{array} \right)^T\).
-

-
- Left Product:
- If \(z \in \mathbf{R}^m\), then the notation \(z^TA\) is the row vector of size \(n\) equal to the transpose of the column vector \(A^Tz \in \mathbf{R}^n\):
- \((z^TA)_j = \sum_{i=1}^m A_{ij}z_i , \;\; j=1, \ldots, n.\)
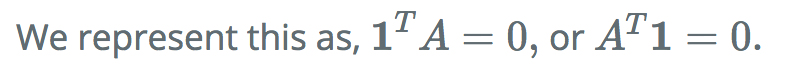
-
- Matrix-matrix product:
- \((AB)_{ij} = \sum_{k=1}^n A_{ik} B_{kj}\).
- where \(A \in \mathbf{R}^{m \times n}\) and \(B \in \mathbf{R}^{n \times p}\), and the notation \(AB\) denotes the \(m \times p\) matrix given above.
- Interpretations:
-
- Transforming the columns of \(B\) into \(Ab_i\):
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ AB = A \left( \begin{array}{ccc} b_1 & \ldots & b_n \end{array} \right) = \left( \begin{array}{ccc} Ab_1 & \ldots & Ab_n \end{array} \right)\) .
where the columns of \(B\) are given by the vectors \(b_i, i=1, \ldots, n\), so that \(B = (b_1 , \ldots, b_n)\). - Transforming the Rows of \(A\) into \(a_i^TB\):
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ AB = \left(\begin{array}{c} a_1^T \\ \vdots \\ a_m^T \end{array}\right) B = \left(\begin{array}{c} a_1^TB \\ \vdots \\ a_m^TB \end{array}\right)\).
where the rows of \(A\) are given by the vectors \(a_i^T, i=1, \ldots, m\): \(A = \left( \begin{array}{c} a_1^T \ldots a_m^T \end{array} \right)^T\).
- Transforming the columns of \(B\) into \(Ab_i\):
-
Block Matrix Products:

-
Outer Products:

-
- Trace:
- The trace of a square \(n \times n\) matrix \(A\), denoted by \(\mathbf{Tr} A\), is the sum of its diagonal elements:
- \(\mathbf{Tr} A = \sum_{i=1}^n A_{ii}\).
- Properties:
- \(\mathbf{Tr} A = \mathbf{Tr} A^T\).
- \(\mathbf{Tr} (AB) = \mathbf{Tr} (BA)\).
- \(\mathbf{Tr}(XYZ) = \mathbf{Tr}(ZXY) = \mathbf{Tr}(YZX)\).
- \({\displaystyle \operatorname{tr} (A+B) = \operatorname{tr} (A)+\operatorname{tr} (B)}\).
- \({\displaystyle \operatorname{tr} (cA) = c\operatorname{tr} (A)}\).
- \({\displaystyle \operatorname{tr} \left(X^{\mathrm {T} }Y\right)=\operatorname{tr} \left(XY^{\mathrm {T} }\right)=\operatorname{tr} \left(Y^{\mathrm {T} }X\right)=\operatorname{tr} \left(YX^{\mathrm {T} }\right)=\sum _{i,j}X_{ij}Y_{ij}}\).
- \({\displaystyle \operatorname{tr} \left(X^{\mathrm {T} }Y\right)=\sum _{ij}(X\circ Y)_{ij}}\ \ \ \\) (The Hadamard product).
- Arbitrary permutations of the product of matrices is not allowed. Only, cyclic permutations are.
However, if products of three symmetric matrices are considered, any permutation is allowed.
- The trace of an idempotent matrix \(A\), is the dimension of A.
- The trace of a nilpotent matrix is zero.
- If \(f(x) = (x − \lambda_1)^{d_1} \cdots (x − \lambda_k)^{d_k}\) is the characteristic polynomial of a matrix \(A\), then \({\displaystyle \operatorname{tr} (A)=d_{1}\lambda_{1} + \cdots + d_{k} \lambda_{k}}\).
- When both \(A\) and \(B\) are \(n \times n\), the trace of the (ring-theoretic) commutator of \(A\) and \(B\) vanishes: \(\mathbf{tr}([A, B]) = 0\); one can state this as “the trace is a map of Lie algebras \({\displaystyle \mathbf{GL_{n}} \to k}\) from operators to scalars”, as the commutator of scalars is trivial (it is an abelian Lie algebra).
- The trace of a projection matrix is the dimension of the target space. \({\displaystyle P_{X} = X\left(X^{\mathrm {T} }X\right)^{-1}X^{\mathrm {T} } \\ \Rightarrow \\ \operatorname {tr} \left(P_{X}\right) = \operatorname {rank} \left(X\right)}\)
-
- Scalar Product:
- \[\langle A, B \rangle := \mathbf{Tr}(A^TB) = \displaystyle\sum_{i=1}^m\sum_{j=1}^n A_{ij}B_{ij}.\]
-
The above definition is Symmetric:
- \[\implies \langle A,B \rangle = \mathbf{Tr} (A^TB) = \mathbf{Tr} (A^TB)^T = \mathbf{Tr} (B^TA) = \langle B,A \rangle .\]
-
We can interpret the matrix scalar product as the vector scalar product between two long vectors of length \(mn\) each, obtained by stacking all the columns of \(A, B\) on top of each other.
- Special Matrices:
- Diagonal matrices: are square matrices \(A\) with \(A_{ij} = 0\) when \(i \ne j\).
- Symmetric matrices: are square matrices that satisfy \(A_{ij} = A_{ji}\)for every pair \((i,j)\).
- Triangular matrices: are square matrices that satisfy \(A_{ij} = A_{ji}\)for every pair \((i,j)\).
Matrix Norms
-
- Norm:
- A matrix norm is a functional
- \[{\displaystyle \|\cdot \|:K^{m\times n}\to \mathbf{R} }\]
- on the vector space \({\displaystyle K^{m\times n}},\) that must satisfy the following properties:
- For all scalars \({\displaystyle \alpha } \in {\displaystyle K}\) and for all matrices \({\displaystyle A}\) and \({\displaystyle B} \in {\displaystyle K^{m\times n}}\),
-
- \(\|\alpha A\|=|\alpha| \|A\|\)
i.e. being absolutely homogeneous
- \(\|\alpha A\|=|\alpha| \|A\|\)
-
- \({\displaystyle \|A+B\|\leq \|A\|+\|B\|}\)
i.e. being sub-additive or satisfying the triangle inequality
- \({\displaystyle \|A+B\|\leq \|A\|+\|B\|}\)
-
- \({\displaystyle \|A\|\geq 0}\)
i.e. being positive-valued
- \({\displaystyle \|A\|\geq 0}\)
-
- \({\displaystyle \|A\|=0} \iff {\displaystyle A=0_{m,n}}\)
i.e. being definite
- \({\displaystyle \|A\|=0} \iff {\displaystyle A=0_{m,n}}\)
-
- \({\displaystyle \|AB\|\leq \|A\|\|B\|}\) for all square matrices \({\displaystyle A}\) and \({\displaystyle B} \in {\displaystyle K^{n\times n}}.\)
Submultiplicativity.
Not satisfied by all Norms.
- \({\displaystyle \|AB\|\leq \|A\|\|B\|}\) for all square matrices \({\displaystyle A}\) and \({\displaystyle B} \in {\displaystyle K^{n\times n}}.\)
-
- \(l_{p,q}\) norms:
- \[{\displaystyle \Vert A\Vert _{p,q}=\left(\sum _{j=1}^{n}\left(\sum _{i=1}^{m}|a_{ij}|^{p}\right)^{q/p}\right)^{1/q}}\]
-
- \(l_{2,1}\):
- \[{\displaystyle \Vert A\Vert _{2,1}= \sum _{j=1}^{n}\left(\sum _{i=1}^{m}|a_{ij}|^{2}\right)^{1/2}}\]
-
- \(l_{2,2}\) (Frobenius norm):
- \[{\displaystyle \|A\|_{\rm {F}}={\sqrt {\sum _{i=1}^{m}\sum _{j=1}^{n}|a_{ij}|^{2}}}={\sqrt {\operatorname {trace} (A^{\dagger }A)}}={\sqrt {\sum _{i=1}^{\min\{m,n\}}\sigma _{i}^{2}(A)}}},\]
- where \({\displaystyle A^{\dagger }}\) denotes the conjugate transpose of \({\displaystyle A}\), and \({\displaystyle \sigma _{i}(A)}\) are the singular values of \({\displaystyle A}\).
- Properties:
-
Submultiplicative.
- Invariant under rotations.
i.e. \({\displaystyle \|A\|_{\rm {F}}^{2}=\|AR\|_{\rm {F}}^{2}=\|RA\|_{\rm {F}}^{2}} {\displaystyle \|A\|_{\rm {F}}^{2}=\|AR\|_{\rm {F}}^{2}=\|RA\|_{\rm {F}}^{2}}\) for any rotation matrix \(R\).
-
Invariant under a unitary transformation for complex matrices.
-
\({\displaystyle \|A^{\rm {T}}A\|_{\rm {F}}=\|AA^{\rm {T}}\|_{\rm {F}}\leq \|A\|_{\rm {F}}^{2}}\).
- \({\displaystyle \|A+B\|_{\rm {F}}^{2}=\|A\|_{\rm {F}}^{2}+\|B\|_{\rm {F}}^{2}+2\langle A,B\rangle _{\mathrm {F} }}\).
-
-
- \(l_{\infty,\infty}\) (Max Norm):
- \[\|A\|_{\max} = \max_{ij} |a_{ij}|.\]
- Properties:
- NOT Submultiplicative.
-
- The Spectral Norm:
- \({\displaystyle \|A\|_{2}={\sqrt {\lambda _{\max }(A^{^{*}}A)}}=\sigma _{\max }(A)} = {\displaystyle \max_{\|x\|_2!=0}(\|Ax\|_2)/(\|x\|_2)}.\)
The spectral norm of a matrix \({\displaystyle A}\) is the largest singular value of \({\displaystyle A}\). i.e. the square root of the largest eigenvalue of the positive-semidefinite matrix \({\displaystyle A^{*}A}.\)
-
- The Spectral Radius of \(A \\) [denoted \(\rho(A)\)]:
- \[\lim_{r\rightarrow\infty}\|A^r\|^{1/r}=\rho(A).\]
- Properties:
-
Submultiplicative.
-
Satisfies, \({\displaystyle \|A^{r}\|^{1/r}\geq \rho (A),}\), where \(\rho(A)\) is the spectral radius of \(A\).
-
It is an “induced vector-norm”.
-
-
Asynchronous:
-
Asynchronous:
-
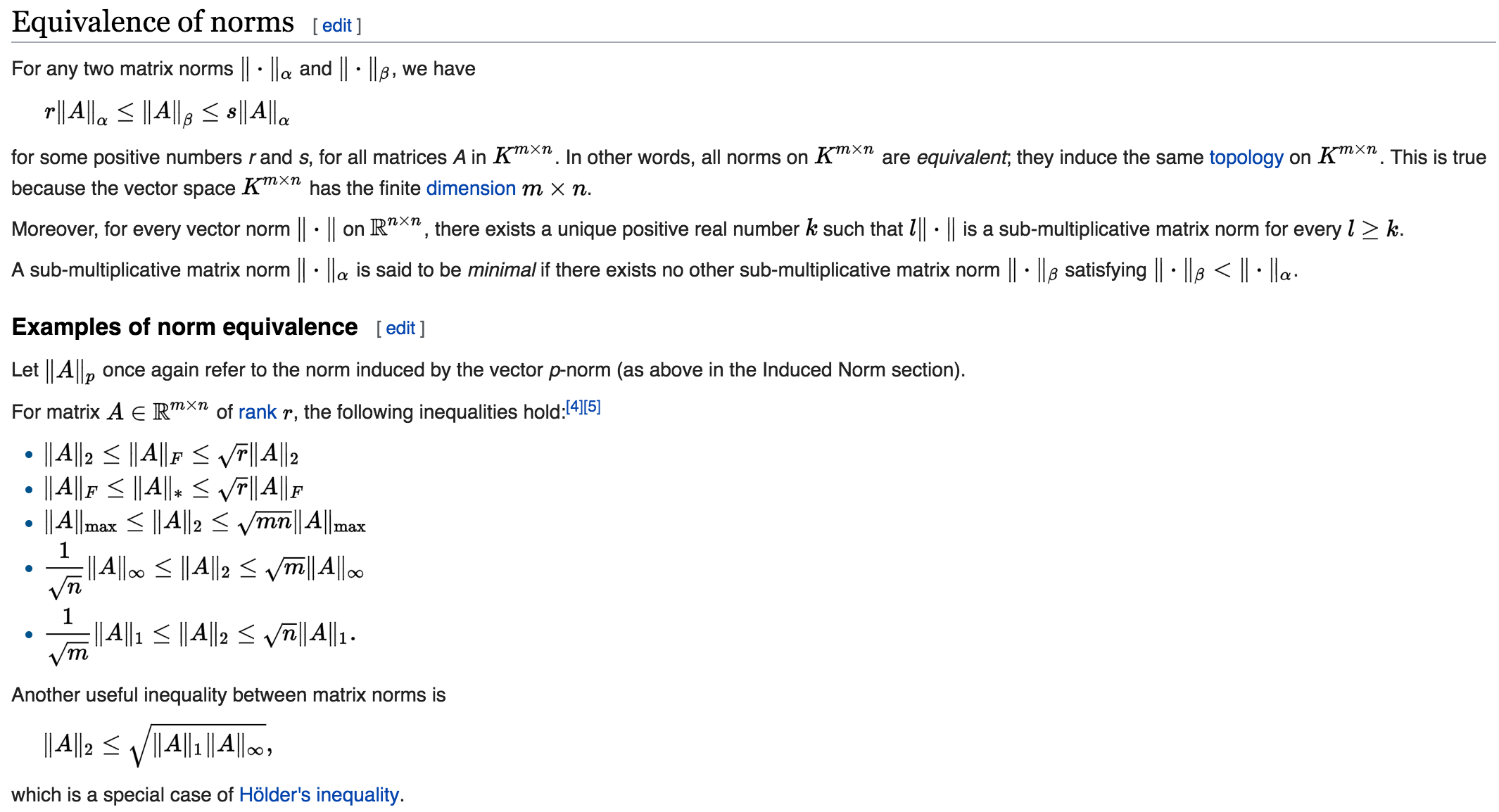
Equivalence of Norms:
- Applications:
-
RMS Gain: Frobenius Norm.
-
Peak Gain: Spectral Norm.
-
Distance between Matrices: Frobenius Norm.

-
Direction of Maximal Variance: Spectral Norm.

-
NOTES
- Distance between 2 vectors (from \(y\) to \(x\)):
\(d = \|x-y\|_2^2\)