Table of Contents

In situations respecting the following assumptions, Semi-Supervised Learning should improve performance: :

Introduction and Preliminaries

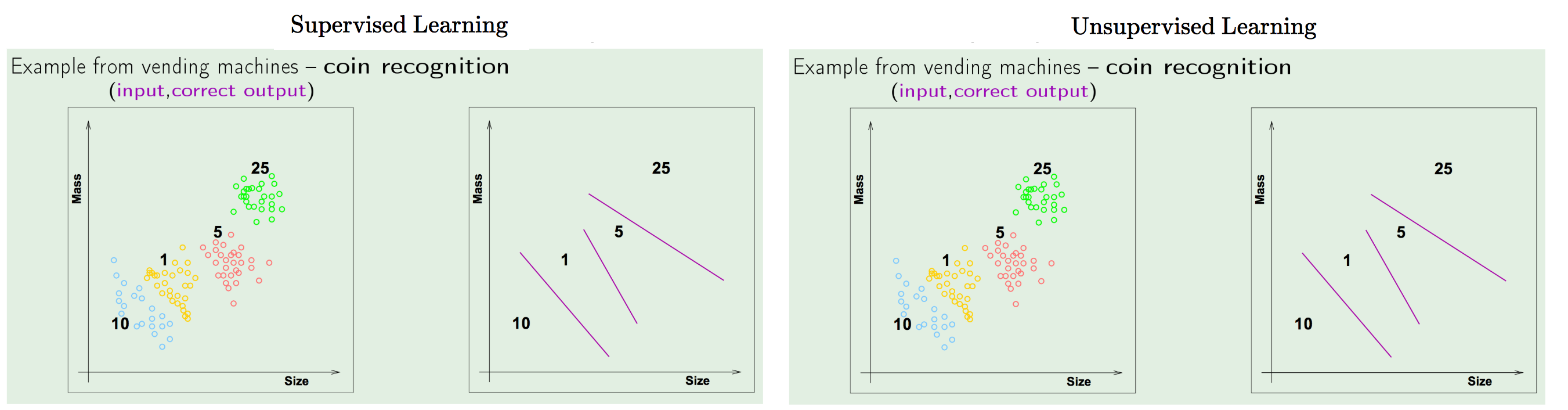
  1. Unsupervised Learning:
    Unsupervised Learning is the task of making inferences, by learning a better representation from some datapoints that do not have any labels associated with them.
    It intends to learn/infer an a priori probability distribution \(p_{X}(x)\); I.E. it solves a density estimation problem.
    It is a type of self-organized Hebbian learning that helps find previously unknown patterns in data set without pre-existing labels.
    img

  2. Density Estimation:
    Density Estimation is a problem in Machine Learning that requires learning a function \(p_{\text {model}} : \mathbb{R}^{n} \rightarrow \mathbb{R}\), where \(p_{\text {model}}(x)\) can be interpreted as a probability density function (if \(x\) is continuous) or a probability mass function (if \(x\) is discrete) on the space that the examples were drawn from.

    To perform such a task well, an algorithm needs to learn the structure of the data it has seen. It must know where examples cluster tightly and where they are unlikely to occur.

    • Types of Density Estimation:
      • Explicit: Explicitly define and solve for \(p_\text{model}(x)\)
      • Implicit: Learn model that can sample from \(p_\text{model}(x)\) without explicitly defining it


  3. Generative Models (GMs):
    A Generative Model is a statistical model of the joint probability distribution on \(X \times Y\):

    $${\displaystyle P(X,Y)}$$

    where \(X\) is an observable variable and \(Y\) is a target variable.

    In supervised settings, a Generative Model is a model of the conditional probability of the observable \(X,\) given a target \(y,\):

    $$P(X | Y=y)$$

    Application - Density Estimation:
    Generative Models address the Density Estimation problem, a core problem in unsupervised learning, since they model
    Given training data, GMs will generate new samples from the same distribution.

    • Types of Density Estimation:
      • Explicit: Explicitly define and solve for \(p_\text{model}(x)\)
      • Implicit: Learn model that can sample from \(p_\text{model}(x)\) without explicitly defining it

    Examples of Generative Models:

    • Gaussian Mixture Model (and other types of mixture model)
    • Hidden Markov Model
    • Probabilistic context-free grammar
    • Bayesian network (e.g. Naive Bayes, Autoregressive Model)
    • Averaged one-dependence estimators
    • Latent Dirichlet allocation (LDA)
    • Boltzmann machine (e.g. Restricted Boltzmann machine, Deep belief network)
    • Variational autoencoder
    • Generative Adversarial Networks
    • Flow-based Generative Model

    Notes:

    • Generative Models are Joint Models.
    • Latent Variables are Random Variables.

Deep Generative Models

  1. Generative Models (GMs):

  2. Deep Generative Models (DGMs):

    • DGMs represent probability distributions over multiple variables in some way:
      • Some allow the probability distribution function to be evaluated explicitly.
      • Others do not allow the evaluation of the probability distribution function but support operations that implicitly require knowledge of it, such as drawing samples from the distribution.
    • Structure/Representation:
      • Some of these models are structured probabilistic models described in terms of graphs and factors, using the language of (probabilistic) graphical models.
      • Others cannot be easily described in terms of factors but represent probability distributions nonetheless.

Likelihood-based Models

  1. Likelihood-based Models:
    Likelihood-based Model: is a statistical model of a joint distribution over data.
    It estimates \(\mathbf{p}_ {\text {data}}\) from samples \(\mathbf{x}^{(1)}, \ldots, \mathbf{x}^{(n)} \sim \mathbf{p}_ {\text {data}}(\mathbf{x})\).
    It Learns a distribution \(p\) that allows:
    • Computing probability of a sample \(p(x)\) for arbitrary \(x\)
    • Sampling \(x \sim p(x)\)
      Sampling is a computable efficient process that generates an RV \(x\) that has the same distribution as a \(p_{\text{data}}\).
      The distribution \(\mathbf{p}_ {\text {data}}\) is just a function that takes as an input a sample \(x\) and outputs the probability of \(x\) under the learned distribution.

    The Goal for Learning Likelihood-based Models:

    Motivation:

    • Solving Hard Problems:
      • Generating Data: synthesizing images, videos, speech, text
      • Compressing Data: constructing efficient codes
      • Anomaly Detection

  2. The Histogram Model:
    The Histogram Model is a very simple likelihood-based model.
    It is a model of discrete data where the samples can take on values in a finite set \(\{1, \ldots, \mathrm{k}\}\).

    The Goal: estimate \(\mathbf{p}_{\text {data}}\) from samples \(\mathbf{x}^{(1)}, \ldots, \mathbf{x}^{(n)} \sim \mathbf{p}_{\text {data}}(\mathbf{x})\).

    The Model: a Histogram

    • Described by \(k\) nonnegative numbers: \(\mathrm{p}_{1}, \ldots, \mathrm{p}_{\mathrm{k}}\)
    • Trained by counting frequencies

      $$\mathrm{p}_ {\mathrm{i}}=(\# \text { times } i \text { appears in the dataset) } /(\#\text { points in the dataset) }$$

    • At Runtime:
      • Inference (querying \(p_i\) for arbitrary \(i\)): simply a lookup into the array \(\mathrm{p}_{1}, \ldots, \mathrm{p}_{\mathrm{k}}\)
      • Sampling (lookup into the inverse cumulative distribution function):
        1. From the model probabilities \(p_{1}, \ldots, p_{k},\) compute the cumulative distribution:

          $$\mathrm{F}_{\mathrm{i}}=\mathrm{p}_ {1}+\cdots+\mathrm{p}_ {\mathrm{i}} \quad$ for all $\mathrm{i} \in\{1, \ldots, \mathrm{k}\}$$

        2. Draw a uniform random number \(u \sim[0,1]\)
        3. Return the smallest \(i\) such that \(u \leq F_{i}\)

    Generalization Problem:

    • The Curse of Dimensionality: Counting fails when there are too many bins and generalization is not achieved.
    • Solution: Function Approximation
      Instead of storing each probability store a parameterized function \(p_{\theta}(x)\).

  3. Achieving Generalization via Function Approximation:
    Function Approximation: Defines a mapping \(p_{\theta}\) from a parameter space to a space of probability distributions.
    E.g. \(\theta\) are the weights of a NN, \(p_{\theta}\) some NN architecture with those weights set.

    Instead of storing each probability store a parameterized function \(p_{\theta}(x)\).
    i.e. Instead of treating the probabilities \(p_1, ..., p_k\) themselves as parameters, we define them to be functions of other parameters \(\theta\).
    The probability of every data point \(p_i = p_{\theta}(x_i)\) will be a function of \(\theta\).
    The mapping is defined such that whenever we update \(\theta\) for any one particular data point, its likely to influence \(p_i\) for other data points that are similar to it.
    We constraint the dimension \(d\) of \(\theta \in \mathbb{R}^d\) to be much less than the number of possible images.
    Such that the parameter space \(\Theta\) is indexing into the low-dimensional space inside the set of all probability distributions.
    This is how we achieve Generalization through function approximation.

    The Revised Goal for Learning Likelihood-based Models - Function Approximation:

    • Original Goal: estimate \(\mathbf{p}_{\text {data}}\) from samples \(\mathbf{x}^{(1)}, \ldots, \mathbf{x}^{(n)} \sim \mathbf{p}_{\text {data}}(\mathbf{x})\).
    • Revised Goal - Function Approximation: Find \(\theta\) (the parameter vector indexing into the distribution space) so that you approximately get the data distribution.
      I.E. Learn \(\theta\) so that \(p_{\theta}(x) \approx p_{\text {data}}(x)\).

    New Challenges:

    • How do we design function approximators to effectively represent complex joint distributions over \(x\), yet remain easy to train?
    • There will be many choices for model design, each with different tradeoffs and different compatibility criteria.
      • Define “what does it mean for one probability distribution to be approximately equal to another”?
        A measure of distance between distributions: distance function.
        It needs to be differentiable wrt \(\theta\), works on finite-datasets, etc.
      • How to “define \(p_{\theta}\)”?
      • How to “learn/optimize \(\theta\)”?
      • How to ensure software-hardware compatibility?

    Designing the model and the training procedure (optimization) go hand-in-hand.

  4. Architecture and Learning in Likelihood-based Models:
    Fitting Distributions:
    • Given data \(\mathbf{x}^{(1)}, \ldots, \mathbf{x}^{(n)}\) sampled from a “true” distribution \(\mathbf{p}_ {\text {data}}\)
    • Set up a model class: a set of parameterized distributions \(\mathrm{p}_ {\theta}\)
    • Pose a search problem over parameters:

      $$\arg \min_ {\theta} \operatorname{loss}\left(\theta, \mathbf{x}^{(1)}, \ldots, \mathbf{x}^{(n)}\right)$$

    • Desiderata - Want the loss function + search procedure to:
      • Work with large datasets (\(n\) is large, say millions of training examples)
      • Yield $\theta$ such that \(p_ {\theta}\) matches \(p_{\text {data}}\) — i.e. the training algorithm “works”.
        Think of the loss as a distance between distributions.
      • Note that the training procedure can only see the empirical data distribution, not the true data distribution: we want the model to generalize.

    Objective - Maximum Likelihood:

    • Maximum Likelihood: given a dataset \(\mathbf{x}^{(1)}, \ldots, \mathbf{x}^{(n)},\) find \(\theta\) by solving the optimization problem

      $$\arg \min _{\theta} \operatorname{loss}\left(\theta, \mathbf{x}^{(1)}, \ldots, \mathbf{x}^{(n)}\right)=\frac{1}{n} \sum_{i=1}^{n}-\log p_{\theta}\left(\mathbf{x}^{(i)}\right)$$

    • Statistics tells us that if the model family is expressive enough and if enough data is given, then solving the maximum likelihood problem will yield parameters that generate the data.
      This is IMPORTANT since one of the main reasons for introducing and using these methods (e.g. MLE) is that they work in practice i.e. leads to an algorithm we can run in practice that actually produces good models.
    • Equivalent to minimizing KL divergence between the empirical data distribution and the model:

      $$\hat{p}_{\text {data }}(\mathbf{x})=\frac{1}{n} \sum_{i=1}^{n} \mathbf{1}\left[\mathbf{x}=\mathbf{x}^{(i)}\right]$$

      $$\mathrm{KL}\left(\hat{p}_{\mathrm{data}} \| p_{\theta}\right)=\mathbb{E}_{\mathbf{x} \sim \hat{p}_{\mathrm{data}}}\left[-\log p_{\theta}(\mathbf{x})\right]-H\left(\hat{p}_ {\mathrm{data}}\right)$$

      I.E. the maximum likelihood objective exactly measures how good of a compressor the model is.

    Optimization - Stochastic Gradient Descent:
    Maximum likelihood is an optimization problem. We use SGD to solve it.

    • SGD minimizes expectations: for \({f}\) a differentiable function of \(\theta,\) it solves

      $$\arg \min_ {\theta} \mathbb{E}[f(\theta)]$$

    • With maximum likelihood (which is an expectation in-of-itself), the optimization problem is

      $$\arg \min _{\theta} \mathbb{E}_{\mathbf{x} \sim \hat{p}_{\text {data }}}\left[-\log p_{\theta}(\mathbf{x})\right]$$

    • Why maximum likelihood + SGD?
      Same Theme: It works with large datasets and is compatible with neural networks.

    Designing the Model:
    Our goal is to design Neural Network models that fit into the maximum likelihood + sgd framework.

    • Key requirement for maximum likelihood + SGD: efficiently compute \(\log p(x)\) and its gradient.
    • The Model \(p_{\theta}\): is chosen to be Deep Neural Networks
      They work in the regime of high expressiveness and efficient computation (assuming specialized hardware).
    • Designing the Networks:
      • Any setting of \(\theta\) must define a valid probability distribution over \(x\):

        $$\forall \theta, \quad \sum_{\mathbf{x}} p_{\theta}(\mathbf{x})=1 \quad \text{ and } \quad p_{\theta}(\mathbf{x}) \geq 0 \quad \forall \mathbf{x}$$

        • Difficulty: The number of terms in the sum is the number of possible data points, thus, it is exponential in the dimension.
          Thus, a naive implementation would have a forward pass w/ exponential time.
        • Energy-based Models do not have this constraint in the model definition, but then have to deal with that constraint in the training algorithm making it very hard to deal with/optimize.
      • \(\log p_{\theta}(x)\) should be easy to evaluate and differentiate with respect to \(\theta\)
      • This can be tricky to set up!

    Bayes Nets and Neural Nets:
    One way to satisfy the condition of defining a valid probability distribution over \(x\) is to model the variables with a Bayes Net.

    Main Idea:
    place a Bayes Net structure (a directed acyclic graph) over the variables in the data, and model the conditional distributions with Neural Networks.

    This Reduces the problem to designing conditional likelihood-based models for single variables.

    We know how to do this: the neural net takes variables being conditioned on as input, and outputs the distribution for the variable being predicted; NNs usually condition on a lot of stuff (features) and predict a single small variable (target \(y\)) this is done in practice all the time in supervised settings (e.g. classification).

    This (the BN representation) yields massive savings in the number of parameters to represent a joint distribution.

    Does this work in practice?

    • Given a Bayes net structure, setting the conditional distributions to neural networks will yield a tractable log likelihood and gradient.
      Great for maximum likelihood training:

      $$\log p_{\theta}(\mathbf{x})=\sum_{i=1}^{d} \log p_{\theta}\left(x_{i} | \text { parents }\left(x_{i}\right)\right)$$

    • Expressiveness: it is completely expressive.
      Assuming a fully expressive Bayes Net structure: any joint distribution can be written as a product of conditionals

      $$\log p(\mathbf{x})=\sum_{i=1}^{d} \log p\left(x_{i} | \mathbf{x}_ {1: i-1}\right)$$

    • This is known as an Autoregressive Model.

    Conclusion:
    An expressive Bayes Net structure with Neural Network conditional distributions yields an expressive model for \(p(x)\) with tractable maximum likelihood training.


  5. Autoregressive Models:

    Notes:

    • Very useful if the problem we are modeling requires a fixed size output (e.g. auto-regressive models).
    • Autoregressive models such as PixelRNN instead train a network that models the conditional distribution of every individual pixel given previous pixels (to the left and to the top). This is similar to plugging the pixels of the image into a char-rnn, but the RNNs run both horizontally and vertically over the image instead of just a 1D sequence of characters.