Table of Contents

Generative Adversarial Networks (GANs)

  1. Auto-Regressive Models VS Variational Auto-Encoders VS GANs:
    Auto-Regressive Models defined a tractable (discrete) density function and, then, optimized the likelihood of training data:

    $$p_\theta(x) = p(x_0) \prod_1^n p(x_i | x_{i<})$$

    While VAEs defined an intractable (continuous) density function with latent variable \(z\):

    $$p_\theta(x) = \int p_\theta(z) p_\theta(x|z) dz$$

    but cannot optimize directly; instead, derive and optimize a lower bound on likelihood instead.

    On the other hand, GANs rejects explicitly defining a probability density function, in favor of only being able to sample.

  2. Generative Adversarial Networks:
    GANs are a class of AI algorithms used in unsupervised machine learning, implemented by a system of two neural networks contesting with each other in a zero-sum game framework.

  3. Motivation:
    • Problem: we want to sample from complex, high-dimensional training distribution; there is no direct way of doing this.
    • Solution: we sample from a simple distribution (e.g. random noise) and learn a transformation that maps to the training distribution, by using a neural network.

    img

    • Generative VS Discriminative: discriminative models had much more success because deep generative models suffered due to the difficulty of approximating many intractable probabilistic computations that arise in maximum likelihood estimation and related strategies, and due to difficulty of leveraging the benefits of piecewise linear units in the generative context.
      GANs propose a new framework for generative model estimation that sidesteps these difficulties.

  4. Structure:
    • Goal:
      estimating generative models that capture the training data distribution
    • Framework:
      an adversarial process in which two models are simultaneously trained a generative model \(G\) that captures the data distribution, and a discriminative model \(D\) that estimates the probability that a sample came from the training data rather than \(G\).
    • Training:
      \(G\) maximizes the probability of \(D\) making a mistake

  5. Training:
    Generator network: try to fool the discriminator by generating real-looking images
    Discriminator network: try to distinguish between real and fake images
    img

    • Train jointly in minimax game.
      • Minimax objective function:

        $$\min _{\theta_{g}} \max _{\theta_{d}}\left[\mathbb{E}_{x \sim p_{\text {data }}} \log D_{\theta_{d}}(x)+\mathbb{E}_{z \sim p(z)} \log \left(1-D_{\theta_{d}}\left(G_{\theta_{g}}(z)\right)\right)\right]$$

        - Discriminator outputs likelihood in \((0,1)\) of real image
        - \(D_{\theta_{d}}(x)\): Discriminator output for real data \(\boldsymbol{x}\)
        - \(D_{\theta_{d}}\left(G_{\theta_{g}}(z)\right)\): Discriminator output for generated fake data \(G(z)\)
        - Discriminator \(\left(\theta_{d}\right)\) wants to maximize objective such that \(\mathrm{D}(\mathrm{x})\) is close to \(1\) (real) and \(\mathrm{D}(\mathrm{G}(\mathrm{z}))\) is close to \(0\) (fake)
        - Generator \(\left(\mathrm{f}_ {\mathrm{g}}\right)\) “wants to minimize objective such that \(\mathrm{D}(\mathrm{G}(\mathrm{z}))\) is close to \(1\) (discriminator is fooled into thinking generated \(\mathrm{G}(\mathrm{z})\) is real)

    • Alternate between*:
      1. Gradient Ascent on Discriminator:

        $$\max _{\theta_{d}}\left[\mathbb{E}_{x \sim p_{\text {data}}} \log D_{\theta_{d}}(x)+\mathbb{E}_{z \sim p(z)} \log \left(1-D_{\theta_{d}}\left(G_{\theta_{g}}(z)\right)\right)\right]$$

      2. Gradient Ascent on Generator (different objective):

        $$\max _{\theta_{g}} \mathbb{E}_{z \sim p(z)} \log \left(D_{\theta_{d}}\left(G_{\theta_{g}}(z)\right)\right)$$

    GAN Training Algorithm:

    - # of Training steps \(\mathrm{k}\): some find \(\mathrm{k}=1\) more stable, others use \(\mathrm{k}>1\) no best rule.

    • Recent work (e.g. Wasserstein GAN) alleviates this problem, better stability!

    img

    Notes:

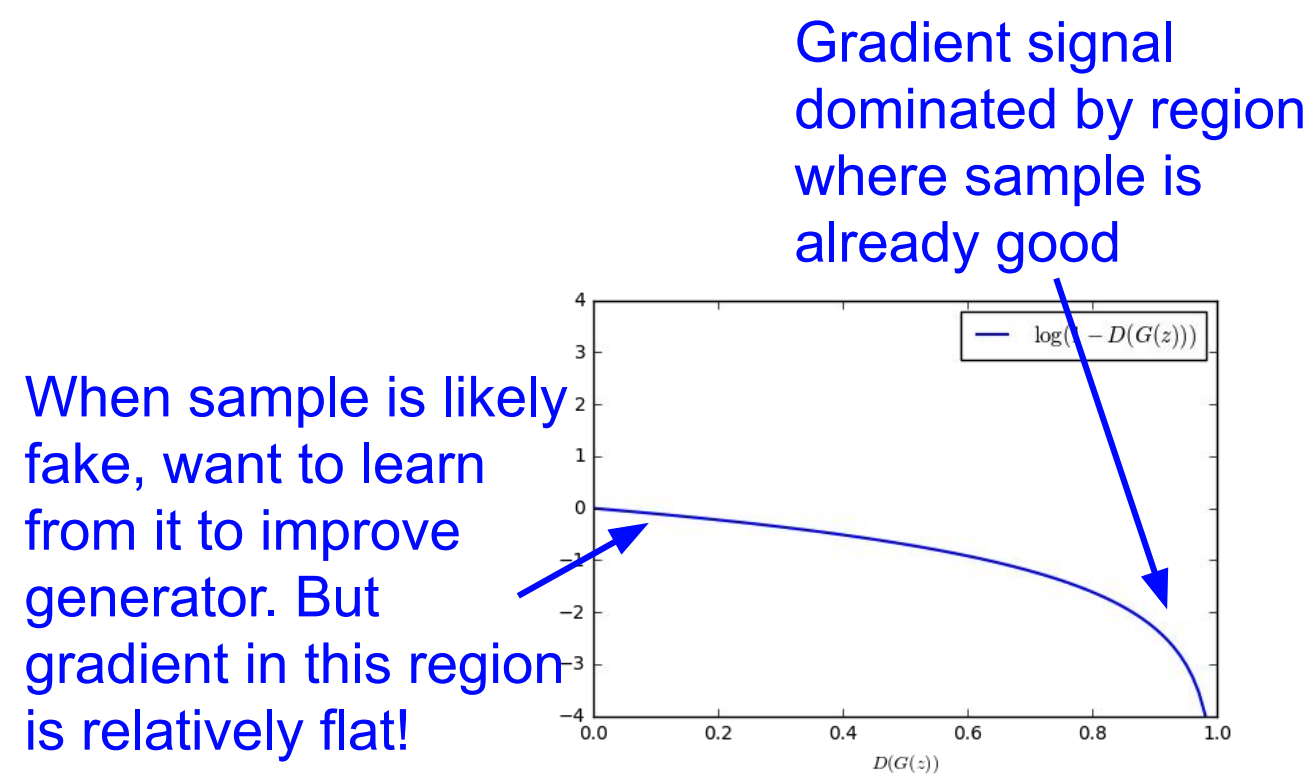
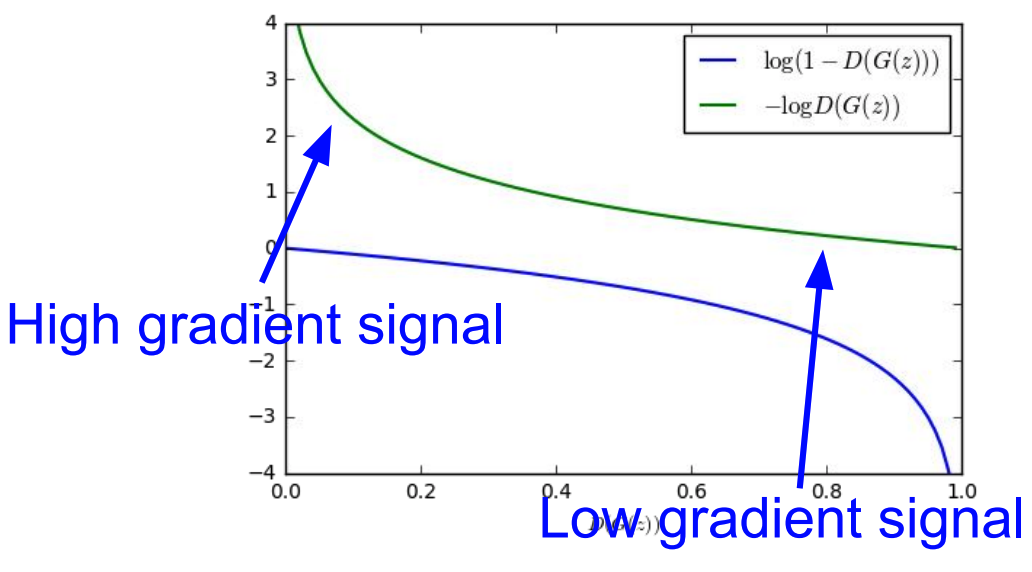
    • * Instead of minimizing likelihood of discriminator being correct, now maximize likelihood of discriminator being wrong. Same objective of fooling discriminator, but now higher gradient signal for bad samples => works much better! Standard in practice.
      • Previously we used to do gradient descent on generator:

        $$\min _{\theta_{g}} \mathbb{E}_{z \sim p(z)} \log \left(1-D_{\theta_{d}}\left(G_{\theta_{g}}(z)\right)\right)$$

        In practice, optimizing this generator objective does not work well.
        img

      • Now we are doing gradient ascent on the generator:

        $$\max _{\theta_{g}} \mathbb{E}_{z \sim p(z)} \log \left(D_{\theta_{d}}\left(G_{\theta_{g}}(z)\right)\right)$$

        img

    • Jointly training two networks is challenging, can be unstable. Choosing objectives with better loss landscapes helps training, is an active area of research.
    • The representations have nice structure:
      • Average \(\boldsymbol{z}\) vectors, do arithmetic:
        img
      • Interpolating between random points in latent space is possible

  6. Generative Adversarial Nets: Convolutional Architectures:
    - Discriminator is a standard convolutional network.
    - Generator is an upsampling network with fractionally-strided convolutions.
    img

    Architecture guidelines for stable Deep Convolutional GANs:

    • Replace any pooling layers with strided convolutions (discriminator) and fractional-strided convolutions (generator).
    • Use batchnorm in both the generator and the discriminator.
    • Remove fully connected hidden layers for deeper architectures.
    • Use ReLU activation in generator for all layers except for the output, which uses Tanh.
    • Use LeakyReLU activation in the discriminator for all layers.

  7. Pros, Cons and Research:
    • Pros:
      • Beautiful, state-of-the-art samples!
    • Cons:
      • Trickier / more unstable to train
      • Can’t solve inference queries such as \(p(x), p(z\vert x)\)
    • Active areas of research:
      • Better loss functions, more stable training (Wasserstein GAN, LSGAN, many others)
      • Conditional GANs, GANs for all kinds of applications

Notes: