Introduction

1. CNNs:

   In machine learning, a convolutional neural network (CNN, or ConvNet) is a class of deep, feed-forward artificial neural networks that has successfully been applied to analyzing visual imagery.

2. The Big Idea:

   CNNs use a variation of multilayer perceptrons designed to require minimal preprocessing.

3. Inspiration Model:

   Convolutional networks were inspired by biological processes in which the connectivity pattern between neurons is inspired by the organization of the animal visual cortex.
   Individual cortical neurons respond to stimuli only in a restricted region of the visual field known as the receptive field. The receptive fields of different neurons partially overlap such that they cover the entire visual field.

4. Design:

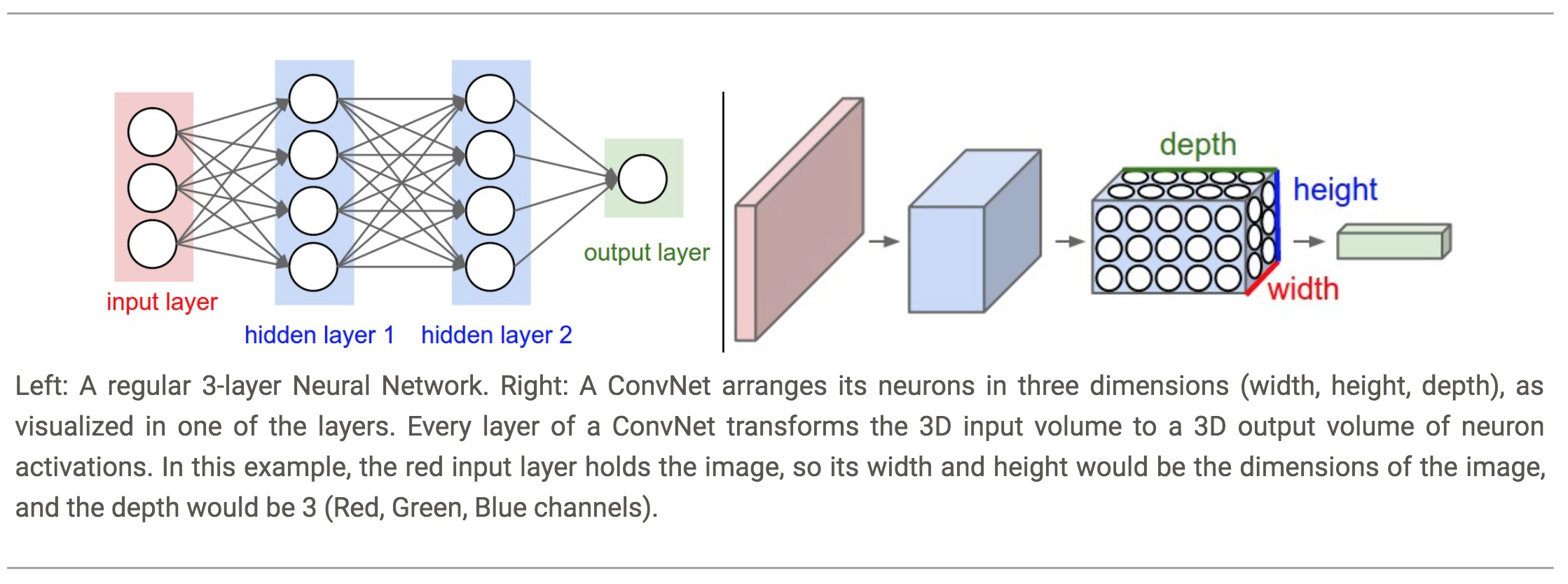
   A CNN consists of an input and an output layer, as well as multiple hidden layers.
   The hidden layers of a CNN typically consist of convolutional layers, pooling layers, fully connected layers and normalization layers.

Architecture and Design

1. Volumes of Neurons:

   Unlike neurons in traditional Feed-Forward networks, the layers of a ConvNet have neurons arranged in 3-dimensions: width, height, depth.

   Note: Depth here refers to the third dimension of an activation volume, not to the depth of a full Neural Network, which can refer to the total number of layers in a network.

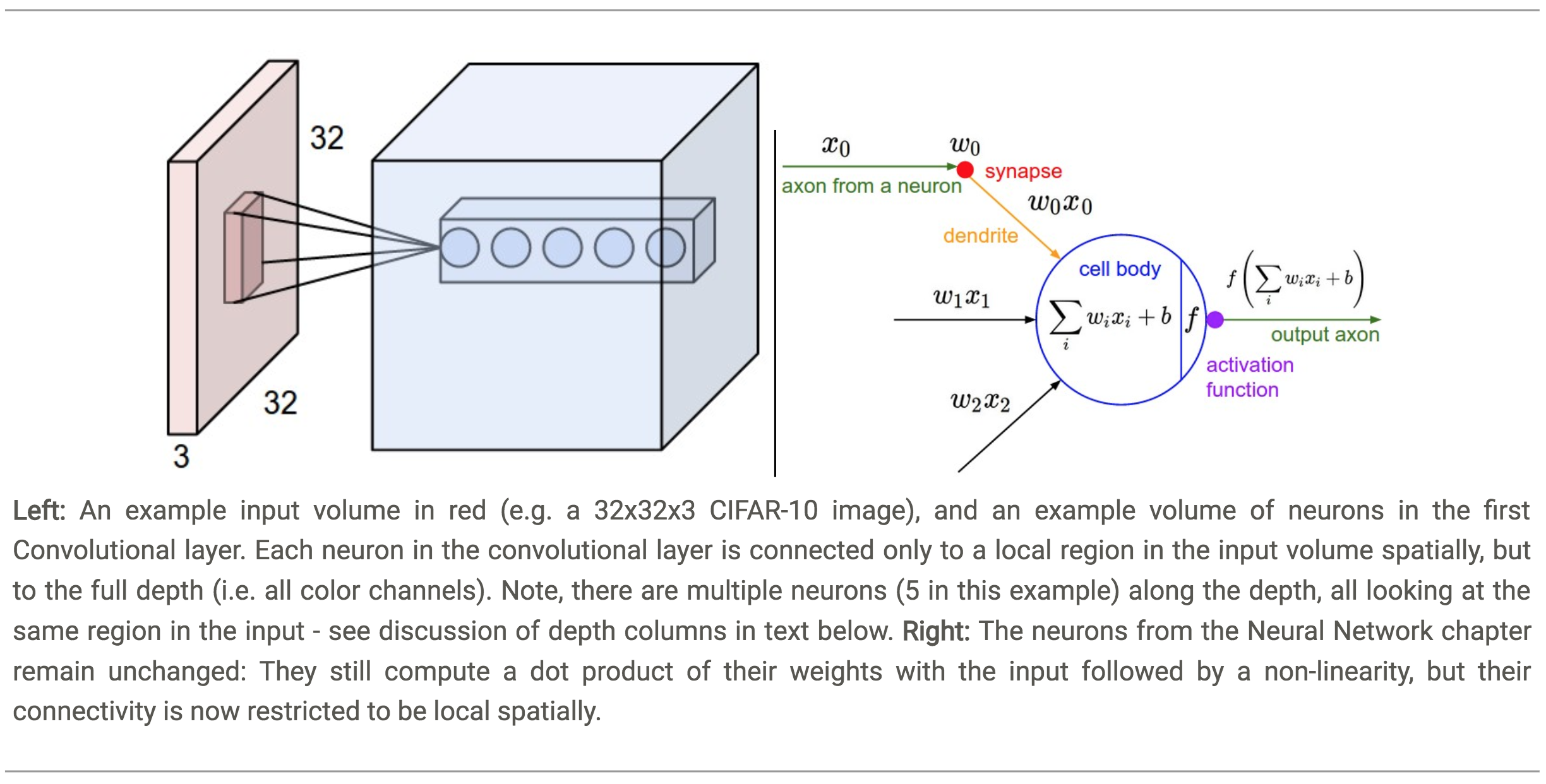
2. Connectivity:

   The neurons in a layer will only be connected to a small region of the layer before it, instead of all of the neurons in a fully-connected manner.

3. Functionality:

   A ConvNet is made up of Layers. Every Layer has a simple API: It transforms an input 3D volume to an output 3D volume with some differentiable function that may or may not have parameters.

   

4. Layers:

   We use three main types of layers to build ConvNet architectures:

   • Convolutional Layer
   • Pooling Layer
   • Fully-Connected Layer

5. Process:

   ConvNets transform the original image layer by layer from the original pixel values to the final class scores.

6. Example Architecture (CIFAR-10):

   Model: [INPUT - CONV - RELU - POOL - FC]

   • INPUT: [32x32x3] will hold the raw pixel values of the image, in this case an image of width 32, height 32, and with three color channels R,G,B.
   • CONV-Layer will compute the output of neurons that are connected to local regions in the input, each computing a dot product between their weights and a small region they are connected to in the input volume.
     This may result in volume such as [\(32\times32\times12\)] if we decided to use 12 filters.
   • RELU-Layer: will apply an element-wise activation function, thresholding at zero. This leaves the size of the volume unchanged ([\(32\times32\times12\)]).
   • POOL-Layer: will perform a down-sampling operation along the spatial dimensions (width, height), resulting in volume such as [\(16\times16\times12\)].
   • Fully-Connected: will compute the class scores, resulting in volume of size [\(1\times1\times10\)], where each of the 10 numbers correspond to a class score, such as among the 10 categories of CIFAR-10.
     As with ordinary Neural Networks and as the name implies, each neuron in this layer will be connected to all the numbers in the previous volume.

7. Fixed Functions VS Hyper-Parameters:

   Some layers contain parameters and other don’t.

   • CONV/FC layers perform transformations that are a function of not only the activations in the input volume, but also of the parameters (the weights and biases of the neurons).

   • RELU/POOL layers will implement a fixed function.

   The parameters in the CONV/FC layers will be trained with gradient descent so that the class scores that the ConvNet computes are consistent with the labels in the training set for each image.

8. Summary:
   • A ConvNet architecture is in the simplest case a list of Layers that transform the image volume into an output volume (e.g. holding the class scores)
   • There are a few distinct types of Layers (e.g. CONV/FC/RELU/POOL are by far the most popular)
   • Each Layer accepts an input 3D volume and transforms it to an output 3D volume through a differentiable function
   • Each Layer may or may not have parameters (e.g. CONV/FC do, RELU/POOL don’t)
   • Each Layer may or may not have additional hyperparameters (e.g. CONV/FC/POOL do, RELU doesn’t)

     Click this for Credits

   

Convolutional Layers

1. Convolutions:

   A Convolution is a mathematical operation on two functions (f and g) to produce a third function, that is typically viewed as a modified version of one of the original functions, giving the integral of the point-wise multiplication of the two functions as a function of the amount that one of the original functions is translated.

   The convolution of the continous functions f and g:

   \[{\displaystyle {\begin{aligned}(f*g)(t)&\,{\stackrel {\mathrm {def} }{=}}\ \int _{-\infty }^{\infty }f(\tau )g(t-\tau )\,d\tau \\&=\int _{-\infty }^{\infty }f(t-\tau )g(\tau )\,d\tau .\end{aligned}}}\]

   The convolution of the discreet functions f and g:

   \[{\displaystyle {\begin{aligned}(f*g)[n]&=\sum _{m=-\infty }^{\infty }f[m]g[n-m]\\&=\sum _{m=-\infty }^{\infty }f[n-m]g[m].\end{aligned}}} (commutativity)\]

2. Cross-Correlation:

   Cross-Correlation is a measure of similarity of two series as a function of the displacement of one relative to the other.

   The continuous cross-correlation on continuous functions f and g:

   \[(f\star g)(\tau )\ {\stackrel {\mathrm {def} }{=}}\int _{-\infty }^{\infty }f^{*}(t)\ g(t+\tau )\,dt,\]

   The discrete cross-correlation on discreet functions f and g:

   \[(f\star g)[n]\ {\stackrel {\mathrm {def} }{=}}\sum _{m=-\infty }^{\infty }f^{*}[m]\ g[m+n].\]

3. Convolutions and Cross-Correlation:

   • Convolution is similar to cross-correlation.
   • For discrete real valued signals, they differ only in a time reversal in one of the signals.
   • For continuous signals, the cross-correlation operator is the adjoint operator of the convolution operator.

4. CNNs, Convolutions, and Cross-Correlation:

   The term Convolution in the name “Convolution Neural Network” is unfortunately a misnomer.
   CNNs actually use Cross-Correlation instead as their similarity operator.
   The term ‘convolution’ has stuck in the name by convention.

5. The Mathematics:

   • The CONV layer’s parameters consist of a set of learnable filters.
     • Every filter is small spatially (along width and height), but extends through the full depth of the input volume.

       For example, a typical filter on a first layer of a ConvNet might have size 5x5x3 (i.e. 5 pixels width and height, and 3 because images have depth 3, the color channels).

   • In the forward pass, we slide (convolve) each filter across the width and height of the input volume and compute dot products between the entries of the filter and the input at any position.
     • As we slide the filter over the width and height of the input volume we will produce a 2-dimensional activation map that gives the responses of that filter at every spatial position.

       Intuitively, the network will learn filters that activate when they see some type of visual feature such as an edge of some orientation or a blotch of some color on the first layer, or eventually entire honeycomb or wheel-like patterns on higher layers of the network.

     • Now, we will have an entire set of filters in each CONV layer (e.g. 12 filters), and each of them will produce a separate 2-dimensional activation map.
   • We will stack these activation maps along the depth dimension and produce the output volume.

   As a result, the network learns filters that activate when it detects some specific type of feature at some spatial position in the input.

6. The Brain Perspective:

   Every entry in the 3D output volume can also be interpreted as an output of a neuron that looks at only a small region in the input and shares parameters with all neurons to the left and right spatially.

7. Local Connectivity:

   • Convolutional networks exploit spatially local correlation by enforcing a local connectivity pattern between neurons of adjacent layers:
     • Each neuron is connected to only a small region of the input volume.
   • The Receptive Field of the neuron defines the extent of this connectivity as a hyperparameter.

     For example, suppose the input volume has size \([32x32x3]\) and the receptive field (or the filter size) is \(5x5\), then each neuron in the Conv Layer will have weights to a \([5x5x3]\) region in the input volume, for a total of \(5*5*3 = 75\) weights (and \(+1\) bias parameter).

   Such an architecture ensures that the learnt filters produce the strongest response to a spatially local input pattern.

8. Spatial Arrangement:

   There are three hyperparameters control the size of the output volume:

   1. The Depth of the output volume is a hyperparameter that corresponds to the number of filters we would like to use (each learning to look for something different in the input).
   2. The Stride controls how depth columns around the spatial dimensions (width and height) are allocated.

      e.g. When the stride is 1 then we move the filters one pixel at a time.

      The Smaller the stride, the more overlapping regions exist and the bigger the volume.
      The bigger the stride, the less overlapping regions exist and the smaller the volume.

   3. The Padding is a hyperparameter whereby we pad the input the input volume with zeros around the border.

      This allows to control the spatial size of the output volumes.

9. The Spatial Size of the Output Volume:

   We compute the spatial size of the output volume as a function of:

   • \(W\): The input volume size.
   • \(F\): \(\:\:\)The receptive field size of the Conv Layer neurons.
   • \(S\): The stride with which they are applied.
   • \(P\): The amount of zero padding used on the border.

   Thus, the Total Size of the Output:

   \[\dfrac{W−F+2P}{S} + 1\]

   • Potential Issue: If this number is not an integer, then the strides are set incorrectly and the neurons cannot be tiled to fit across the input volume in a symmetric way.

   • Fix: In general, setting zero padding to be \({\displaystyle P = \dfrac{K-1}{2}}\) when the stride is \({\displaystyle S = 1}\) ensures that the input volume and output volume will have the same size spatially.

10. The Convolution Layer:

    

Layers

1. Convolution Layer:

   One image becomes a stack of filtered images.

Distinguishing features

1. Asynchronous:

2. Image Features:

   are certain quantities that are calculated from the image to better describe the information in the image, and to reduce the size of the input vectors.

   • Examples:
     • Color Histogram: Compute a (bucket-based) vector of colors with their respective amounts in the image.
     • Histogram of Oriented Gradients (HOG): we count the occurrences of gradient orientation in localized portions of the image.
     • Bag of Words: a bag of visual words is a vector of occurrence counts of a vocabulary of local image features.

       The visual words can be extracted using a clustering algorithm; K-Means.