Table of Contents

Feature Extraction (Notes - Docs)
Audio Compression

Introduction

  1. ML-based Compression:
    The main idea behind ML-based compression is that structure is automatically discovered instead of manually engineered.
    • Examples:
      • DjVu: employs segmentation and K-means clustering to separate foreground from background and analyze the documents contents.

WaveOne

Further Reading

WaveOne is a machine learning-based approach to lossy image compression.

  1. Main Idea:
    An ML-based approach to compression that utilizes the older techniques for quantization but with an encoder-decoder model that depends on adversarial training for a higher quality reconstruction.
  2. Model:
    The model includes three main steps that are layered together in one pipeline:
    • Feature Extraction: an approach that aims to recognize the different types of structures in an image.
      • Structures:
        • Across input channels
        • Within individual scales
        • Across Scales
      • Methods:
        • Pyramidal Decomposition: for analyzing individual scales
        • Interscale Alignment Procedure: for exploiting structure shared across scales
    • Code Computation and Regularization: a module responsible for further compressing the extracted features by *quantizing the features and encoding them via two methods.
      • Methods:
        • Adaptive Arithmetic Coding Scheme: applied on the features binary expansions
        • Adaptive Codelength Regularization: to penalize the entropy of the features to achieve better compression
    • Adversarial Training (Discriminator Loss): a module responsible for enforcing realistic reconstructions.
      • Methods:
        • Adaptive Arithmetic Coding Scheme: applied on the features binary expansions
        • Adaptive Codelength Regularization: to penalize the entropy of the features to achieve better compression
  3. Feature Extraction:
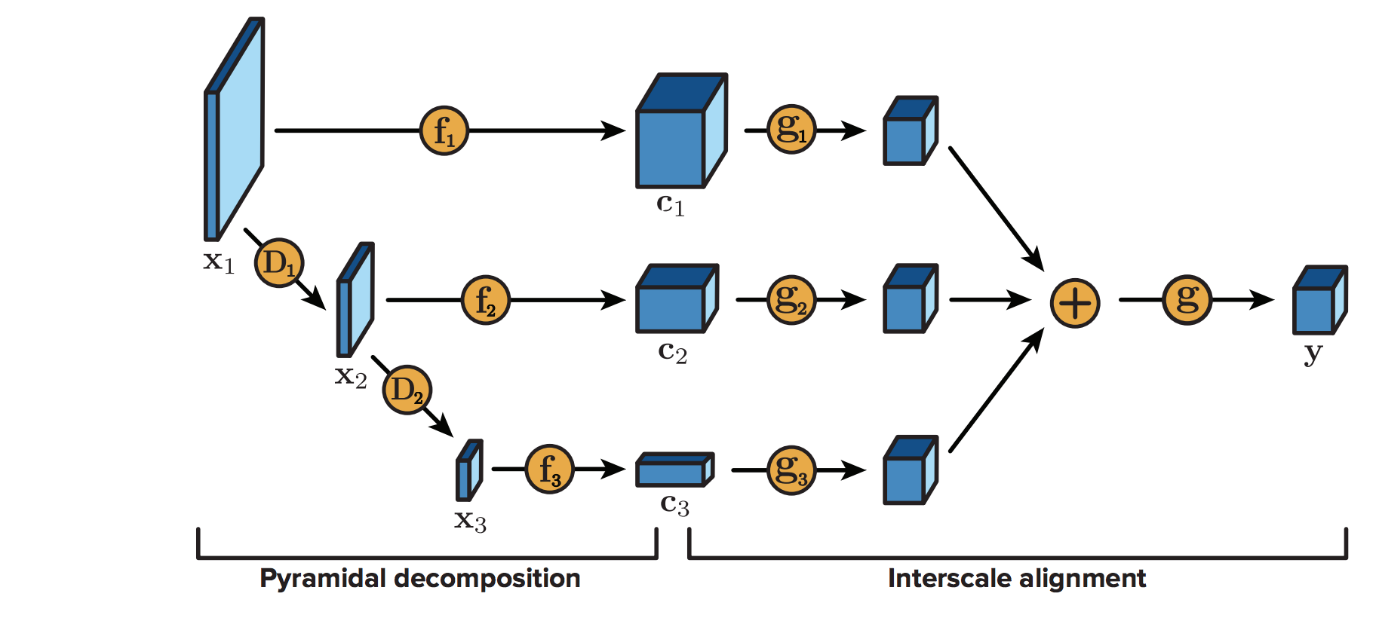
    • Pyramidal Decomposition:
      Inspired by the use of wavelets for multiresolution analysis, in which an input is analyzed recursively via feature extraction and downsampling operators, the pyramidal decomposition encoder generalizes the wavelet decomposition idea to learn optimal, nonlinear extractors individually for each scale.
      For each input \(\mathbf{x}\) to the model, and a total of \(M\) scales, denote the input to scale \(m\) by \(\mathbf{x}_m\).
      • Algorithm:
        • Set input to first scale \(\mathbf{x}_1 = \mathbf{x}\)
        • For each scale \(m\):
          • Extract coefficients \(\mathbf{c}_m = \mathbf{f}_m(\mathbf{x}_m) \in \mathbb{R}^{C_m \times H_m \times W_m}\) via some parametrized function \(\mathbf{f}_m(\dot)\) for output channels \(C_m\), height \(H_m\) and width \(W_m\)
          • Compute the input to the next scale as \(\mathbf{x}_{m+1} = \mathbf{D}_m(\mathbf{x}_m)\), where \(\mathbf{D}_m(\dot)\) is some downsampling operator (either fixed or learned)

      Typically, \(M\) is chosen to be \(= 6\) scales.
      The feature extractors for the individual scales are composed of a sequence of convolutions with kernels \(3 \times 3\) or \(1 \times 1\) and ReLUs with a leak of \(0.2\).
      All downsamplers are learned as \(4 \times 4\) convolutions with a stride of \(2\).

    img
    • Interscale Alignment:
      Designed to leverage information shared across different scales — a benefit not offered by the classic wavelet analysis.
      • Structure:
        • Input: the set of coefficients extracted from the different scales \(\{\mathbf{c}_m\}_{m=1}^M \subset \mathbb{R}^{C_m \times H_m \times W_m}\)
        • Output: a tensor \(\mathbf{y} \in \mathbb{R}^{C \times H \times W}\)
      • Algorithm:
        • Map each input tensor \(\mathbf{c}_m\) to the target dimensionality via some parametrized function \(\mathbf{g}_m(·)\): this involves ensuring that this function spatially resamples \(\mathbf{c}_m\) to the appropriate output map size \(H \times W\), and ouputs the appropriate number of channels \(C\)
        • Sum \(\mathbf{g}_m(\mathbf{c}_m) = 1, \ldots, M\), and apply another parameterized non-linear transformation \(\mathbf{g}(·)\) for joint processing
          \(\mathbf{g}_m(·)\) is chosen as a convolution or a deconvolution with an appropriate stride to produce the target spatial map size \(H \times W\).
          \(\mathbf{g}(·)\) is choses as a sequence of \(3 \times 3\) convolutions.
  4. Code Computation and Regularization:
    Given the output tensor \(\mathbf{y} \in \mathbb{R}^{C \times H \times W}\) of the feature extraction step (namely alignment), we proceed to quantize and encode it.
    • Quantization: the tensor \(\mathbf{y}\) is quantized to bit precision \(B\):
      img
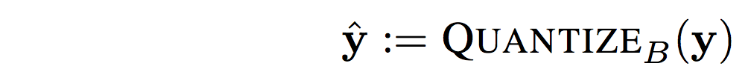
      Given a desired precision of \(B\) bits, we quantize the feature tensor into \(2^B\) equal-sized bins as:
      img
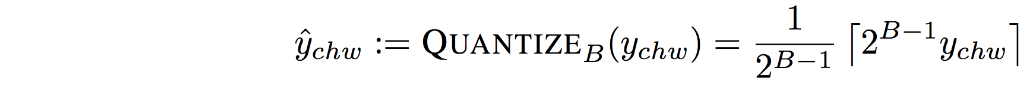
      For the special case \(B = 1\), this reduces exactly to a binary quantization scheme.
      In-practice \(B = 6\) is chosen as a smoother quantization method.
      • Reason:
        Mapping the continuous input values representing the image signal to a smaller countable set to achieve a desired precision of \(B\) bits

    • Bitplane Decomposition: we transform the quantized tensor \(\mathbf{\hat{y}}\) into a binary tensor suitable for encoding via a lossless bitplane decomposition:
      img
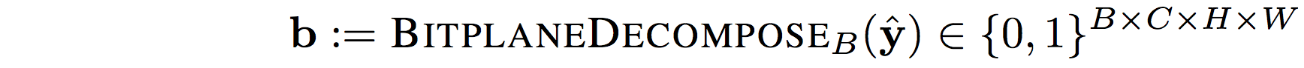
      \(\mathbf{\hat{y}}\) is decomposed into bitplanes by a transformation that maps each value \(\hat{y}_{chw}\) into its binary expansion of \(B\) bits.
      Hence, each of the \(C\) spatial maps \(\mathbf{\hat{y}}_c \in \mathbb{R}^{H \times W}\) of \(\mathbf{\hat{y}}\) expands into \(B\) binary bitplanes.

      • Reason:
        This decomposition enables the entropy coder to exploit structure in the distribution of the activations in \(\mathbf{y}\) to achieve a compact representation.
    • Adaptive Arithmetic Encoding: encodes \(\mathbf{b}\) into its final variable-length binary sequence \(\mathbf{s}\) of length \(\mathcal{l}(\mathbf{s})\):
      img
      • The binary tensor \(\mathbf{b}\) that is produced by the bitplane decomposition contains significant structure (e.g. higher bitplanes are sparser, and spatially neighboring bits often have the same value).
        This structure can be exploited by using Adaptive Arithmetic Encoding.
      • Method:
        • Encoding:
          Associate each bit location in the binary tensor \(\mathbf{b}\) with a context, which comprises a set of features indicative of the bit value.
          The features are based on the position of the bit and the values of neighboring bits.
          To predict the value of each bit from its context features, we _train a classifier           and use its output probabilities to compress \(\mathbf{b}\) via arithmetic coding.
        • Decoding:
          At decoding time, we perform the inverse operation to decompress the code.
          We interleave between:
          • Computing the context of a particular bit using the values of previously decoded bits
          • Using this context to retrieve the activation probability of the bit and decode it

            This operation constrains the context of each bit to only include features composed of bits already decoded

      • Reason:
        We aim to leverage the structure in the data, specifically in the binary tensor \(\mathbf{b}\) produced by the bitplane decomposition which has low entropy
    • Adaptive Codelength Regularization: modulates the distribution of the quantized representation \(\mathbf{\hat{y}}\) to achieve a target expected bit count across inputs:
      img
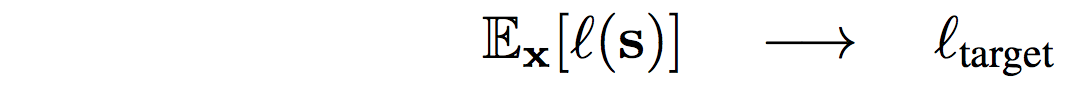
      • Goal: regulate the expected codelength \(\mathbb{E}_x[\mathcal{l}(\mathbf{s})]\) to a target value \(\mathcal{l}_{\text{target}}\).
      • Method:
        We design a penalty that encourages a structure that the AAC is able to encode.
        Namely, we regularize the quantized tensor \(\mathbf{\hat{y}}\) with:
        img
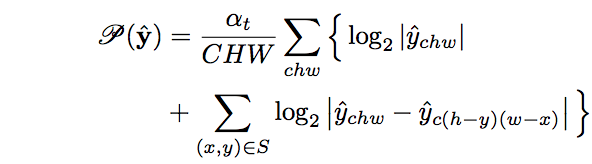
        for iteration \(t\) and difference index set \(S = \{(0,1), (1,0), (1,1), (-1,1)\}\).

        The first term penalizes the magnitude of each tensor element
        The Second Term penalizes deviations between spatial neighbors

      • Reason:
        The Adaptive Codelength Regularization is designed to solve one problem; the non-variability of the latent space code, which is what controls (defines) the bitrate.
        It, essentially, allows us to have latent-space codes with different lengths, depending on the complexity of the input, by enabling better prediction by the AAX
        In practice, a total-to-target ratio \(= BCHW/\mathcal{l}_{\text{target}} = 4\) works well.
  5. Adversarial Train:
    • GAN Architecture:
      • Generator: Encoder-Decoder Pipeline
      • Discriminator: Classification ConvNet
    • Discriminator Design:
  6. Architecture:
    • Problem: Regression Problem
    • Goal: Learn a function \(\psi(x;\theta)\) that is trained and used to regress to a pose vector.
    • Estimation: \(\psi\) is based on (learned through) Deep Neural Net
    • Deep Neural Net: is a Convolutional Neural Network; namely, AlexNet
      • Input: image with pre-defined size \(= \:\) #-pixels \(\times 3\)-color channels

        \((220 \times 220)\) with a stride of \(4\)

      • Output: target value of the regression\(= 2k\) joint coordinates

    Denote by \(\mathbf{C}\) a convolutional layer, by \(\mathbf{LRN}\) a local response normalization layer, \(\mathbf{P}\) a pooling layer and by \(\mathbf{F}\) a fully connected layer

    For \(\mathbf{C}\) layers, the size is defined as width \(\times\) height \(\times\) depth, where the first two dimensions have a spatial meaning while the depth defines the number of filters.

    • Alex-Net:
      • Architecture: \(\mathbf{C}(55 \times 55 \times 96) − \mathbf{LRN} − \mathbf{P} − \mathbf{C}(27 \times 27 \times 256) − \mathbf{LRN} − \mathbf{P} − \\\mathbf{C}(13 \times 13 \times 384) − \mathbf{C}(13 \times 13 \times 384) − \mathbf{C}(13 \times 13 \times 256) − \mathbf{P} − \mathbf{F}(4096) − \mathbf{F}(4096)\)
      • Filters:
        • \(\mathbf{C}_{1} = 11 \times 11\),
        • \(\mathbf{C}_{2} = 5 \times 5\),
        • \(\mathbf{C}_{3-5} = 3 \times 3\).
      • Total Number of Parameters \(= 40\)M
      • Training Dataset:
        Denote by \(D\) the training set and \(D_N\) the normalized training set:
        \(\ \ \ \ \ \ \ \ \ \ \ \ \ \\) \(\ \ \ \ \ \ \ \ \ \ \ \ \ \\) \(D_N = \{(N(x),N(\mathbf{y}))\vert (x,\mathbf{y}) \in D\}\)
      • Loss: the Loss is modified; instead of a classification loss, we train a linear regression on top of the last network layer to predict a pose vector by minimizing \(L_2\) distance between the prediction and the true pose vector,
    \[\arg \min_\theta \sum_{(x,y) \in D_N} \sum_{i=1}^k \|\mathbf{y}_i - \psi_i(x;\theta)\|_2^2\]
    • Optimization:
      • BackPropagation in a distributed online implementation
      • Adaptive Gradient Updates
      • Learning Rate \(= 0.0005 = 5\times 10^{-4}\)
      • Data Augmentation: randomly translated image crops, left/right flips
      • DropOut Regularization for the \(\mathbf{F}\) layers \(= 0.6\)
  7. Architecture:
    • Motivation:
      Although, the pose formulation of the DNN has the advantage that the joint estimation is based on the full image and thus relies on context, due its fixed input size of \(220 \times 220\), the network has limited capacity to look at detail - it learns filters capturing pose properties at coarse scale.
      The pose properties are necessary to estimate rough pose but insufficient to always precisely localize the body joints.
      Increasing the input size is infeasible since it will increase the already large number of parameters.
      Thus, a cascade of pose regressors is used to achieve better precision.
    • Structure and Training:
      At the first stage:
      • The cascade starts off by estimating an initial pose as outlined in the previous section.
        At subsequent stages:
      • Additional DNN regressors are trained to predict a displacement of the joint locations from previous stage to the true location.

        Thus, each subsequent stage can be thought of as a refinement of the currently predicted pose.

      • Each subsequent stage uses the predicted joint locations to focus on the relevant parts of the image – subimages are cropped around the predicted joint location from previous stage and the pose displacement regressor for this joint is applied on this sub-image.

        Thus, subsequent pose regressors see higher resolution images and thus learn features for finer scales which ultimately leads to higher precision

    • Method and Architecture:
      • The same network architecture is used for all stages of the cascade but learn different parameters.
      • Start with a bounding box \(b^0\): which either encloses the full image or is obtained by a person detector
      • Obtain an initial pose:
        Stage 1: \(\mathbf{y}^1 \leftarrow N^{-1}(\psi(N(x;b^0);\theta_1);b^0)\)
      • At stages \(s \geq 2\), for all joints:
        • Regress first towards a refinement displacement \(\mathbf{y}_i^s - \mathbf{y}_i^{(s-1)}\) by applying a regressor on the sub image defined by \(b_i^{(s-1)}\)
        • Estimate new joint boxes \(b_i^s\):
          Stage \(s\): \(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{y}_i^s \leftarrow \mathbf{y}_i^{(2-1)} + N^{-1}(\psi(N(x;b^0);\theta_s);b) \:\: (6) \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \:\:\:\: \text{for } b = b_i^(s-1) \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ b_i^s \leftarrow (\mathbf{y}_i^s, \sigma diam(\mathbf{y}^s), \sigma diam(\mathbf{y}^s))) \:\: (7)\)
          where we considered a joint bounding box \(b_i\) capturing the sub-image around \(\mathbf{y}_i: b_i(\mathbf{y}; \sigma) = (\mathbf{y}_i, \sigma diam(\mathbf{y}), \sigma diam(\mathbf{y}))\) having as center the i-th joint and as dimension the pose diameter scaled by \(\sigma\), to refine a given joint location \(\mathbf{y}_i\).
      • Apply the cascade for a fixed number of stages \(= S\)
    • Loss: (at each stage \(s\))
    \[\theta_s = \arg \min_\theta \sum_{(x,\mathbf{y}_i) \in D_A^s} \|\mathbf{y}_i - \psi_i(x;\theta)\|_2^2 \:\:\:\:\: (8)\]
  8. Advantages:
    • The DNN is capable of capturing the full context of each body joint
    • The approach is simpler to formulate than graphical-models methods - no need to explicitly design feature representations and detectors for parts or to explicitly design a model topology and interactions between joints.

      Instead a generic ConvNet learns these representations

  9. Notes:
    • The use of a generic DNN architecture is motivated by its outstanding results on both classification and localization problems and translates well to pose estimation
    • Such a model is a truly holistic one — the final joint location estimate is based on a complex nonlinear transformation of the full image
    • The use of a DNN obviates the need to design a domain specific pose model
    • Although the regression loss does not model explicit interactions between joints, such are implicitly captured by all of the 7 hidden layers – all the internal features are shared by all joint regressors

Proposed Changes

  1. Gated-Matrix Selection for Latent Space dimensionality estimation and Dynamic bit-rate modification:
  2. Conditional Generative-Adversarial Training with Random-Forests for Generalizable domain-compression:
  3. Adversarial Feature Learning for Induced Natural Representation and Artifact Removal:

Papers:

  1. WaveOne Paper: https://arxiv.org/pdf/1705.05823.pdf Site: http://www.wave.one/ Post: http://www.wave.one/icml2017
  2. Generative Compression – Santurker, Budden, Shavit (MIT) Paper: https://arxiv.org/pdf/1703.01467.pdf
  3. Toward Conceptual Compression – DeepMind Paper: https://papers.nips.cc/paper/6542-towards-conceptual-compression.pdf