Optimizing Gradient Descent
Blog: SGD, Momentum and Adaptive Learning Rate
EE227C Notes: Convex Optimization and Approximation
Convex Functions
Strong Convexity
Lipschitz continuous gradient (condition)
Conjugate Gradient
NOTES ON FIRST-ORDER METHODS FOR MINIMIZING SMOOTH FUNCTIONS
Gradient Descent (paperspace)
An Intuitive Introduction to the Hessian for Deep Learning
NIPS Optimization Lecture!!
10 Gradient Descent Optimisation Algorithms + Cheat Sheet (Blog!)

Gradient-Based Optimization

1. Gradient-Based Optimization:
   Gradient Methods are algorithms to solve problems of the form:

   $$\min_{x \in \mathbb{R}^{n}} f(x)$$

   with the search directions defined by the gradient of the function at the current point.
   
   

2. Gradient-Based Algorithms:
   Examples, include:
   • Gradient Descent: minimizes arbitrary differentiable functions.
   • Conjugate Gradient: minimizes sparse linear systems w/ symmetric & positive-definite matrices.
   • Coordinate Descent: minimizes functions of two variables.
     
     

Gradient Descent

1. Gradient Descent:
   Gradient Descent is a first-order, iterative algorithm to minimize an objective function \(J(\theta)\) parameterized by a model’s parameters \(\theta \in \mathbb{R}^{d}\) by updating the parameters in the opposite direction of the gradient of the objective function \(\nabla_{\theta} J(\theta)\) w.r.t. to the parameters.
   
   

   Intuition (for derivation):

   1. Local Search from a starting location on a hill
   2. Feel around how a small movement/step around your location would change the height of the surrounding hill (is the ground higher or lower)
   3. Make the movement/step consistent as a small fixed step along some direction
   4. Measure the steepness of the hill at the new location in the chosen direction
   5. Do so by Approximating the steepness with some local information
   6. Find the direction that decreases the steepness the most

   \(\iff\)

   1. Local Search from an initial point \(x_0\) on a function
   2. Explore the value of the function at different small nudges around \(x_0\)
   3. Make the nudges consistent as a small fixed step \(\delta\) along a normalized direction \(\hat{\boldsymbol{u}}\)
   4. Evaluate the function at the new location \(x_0 + \delta \hat{\boldsymbol{u}}\)
   5. Do so by Approximating the function w/ first-order information (Taylor expansion)
   6. Find the direction \(\hat{\boldsymbol{u}}\) that minimizes the function the most
      
      
2. Derivation:
   A small change in \(\boldsymbol{x}\):
   We would like to know how would a small change in \(\boldsymbol{x}\), namely \(\Delta \boldsymbol{x}\) would affect the value of the function \(f(x)\). This will allow us to evaluate the function:

   $$f(\mathbf{x}+\Delta \mathbf{x})$$

   to find the direction that makes \(f\) decrease the fastest.

   Let’s set up \(\Delta \boldsymbol{x}\), the change in \(\boldsymbol{x}\), as a fixed step \(\delta\) along some normalized direction \(\hat{\boldsymbol{u}}\):

   $$\Delta \boldsymbol{x} = \delta \hat{\boldsymbol{u}}$$

   The Gradient:
   The gradient tells us how that small change in \(f(\mathbf{x}+\Delta \mathbf{x})\) affects \(f\) through the first-order approximation:

   $$f(\mathbf{x}+\Delta \mathbf{x}) \approx f(\mathbf{x})+\Delta \mathbf{x}^{T} \nabla_{\mathbf{x}} f(\mathbf{x})$$

   In the single variable case, \(f(x+\delta) \approx f(x)+\delta f'(x)\), we know that \(f\left(x-\delta \operatorname{sign}\left(f^{\prime}(x)\right)\right)\) is less than \(f(x)\) for small enough \(\delta\).
   We can thus reduce \(f(x)\) by moving \(x\) in small steps with the opposite sign of the derivative.

   The Change in \(f\):
   The change in the objective function is:

   $$\begin{aligned} \Delta f &= f(\boldsymbol{x}_ 0 + \Delta \boldsymbol{x}) - f(\boldsymbol{x}_ 0) \\ &= f(\boldsymbol{x}_ 0 + \delta \hat{\boldsymbol{u}}) - f(\boldsymbol{x}_ 0)\\ &= \delta \nabla_x f(\boldsymbol{x}_ 0)^T\hat{\boldsymbol{u}} + \mathcal{O}(\delta^2) \\ &= \delta \nabla_x f(\boldsymbol{x}_ 0)^T\hat{\boldsymbol{u}} \\ &\geq -\delta\|\nabla f(\boldsymbol{x}_ 0)\|_ 2 \end{aligned} $$

   using the first order approximation above.
   Notice:

   $$\nabla_x f(\boldsymbol{x}_ 0)^T\hat{\boldsymbol{u}} \in \left[-\|\nabla f(\boldsymbol{x}_ 0)\|_ 2, \|\nabla f(\boldsymbol{x}_ 0)\|_ 2\right]$$

   since \(\hat{\boldsymbol{u}}\) is a unit vector; either aligned with \(\nabla_x f(\boldsymbol{x}_ 0)\) or in the opposite direction; it contributes nothing to the magnitude of the dot product.

   So, the \(\hat{\boldsymbol{u}}\) that changes the above inequality to equality, achieves the largest negative value (moves the most downhill). That vector \(\hat{\boldsymbol{u}}\) is, then, the one in the negative direction of \(\nabla_x f(\boldsymbol{x}_ 0)\); the opposite direction of the gradient.

   The Directional Derivative:
   The directional derivative in direction \(\boldsymbol{u}\) (a unit vector) is the slope of the function \(f\) in direction \(\boldsymbol{u}\). In other words, the directional derivative is the derivative of the function \(f(\boldsymbol{x}+\alpha \boldsymbol{u})\) with respect to \(\delta\), evaluated at \(\delta= 0\).
   Using the chain rule, we can see that \(\frac{\partial}{\partial \delta} f(\boldsymbol{x}+\delta \boldsymbol{u})\) evaluates to \(\boldsymbol{u}^{\top} \nabla_{\boldsymbol{x}} f(\boldsymbol{x})\) when \(\delta=0\).

   Minimizing \(f\):
   To minimize \(f\), we would like to find the direction in which \(f\) decreases the fastest. We do so by using the directional derivative:

   $$\begin{aligned} & \min _{\boldsymbol{u}, \boldsymbol{u}^{\top} \boldsymbol{u}=1} \boldsymbol{u}^{\top} \nabla_{\boldsymbol{x}} f(\boldsymbol{x}) \\ =& \min_{\boldsymbol{u}, \boldsymbol{u}^{\top} \boldsymbol{u}=1}\|\boldsymbol{u}\|_{2}\left\|\nabla_{\boldsymbol{x}} f(\boldsymbol{x})\right\|_{2} \cos \theta \\ =& \min_{\boldsymbol{u}} \cos \theta \\ \implies& \boldsymbol{u} = -\nabla_x f(x)\end{aligned}$$

   by substituting \(\|\boldsymbol{u}\|_2 = 1\) and ignoring factors that do not depend on \(\boldsymbol{u}\), we get \(\min_{\boldsymbol{u}} \cos \theta\); this is minimized when \(\boldsymbol{u}\) points in the opposite direction as the gradient.
   Or rather, because \(\hat{\boldsymbol{u}}\) is a unit vector, we need:

   $$\hat{\boldsymbol{u}} = - \dfrac{\nabla_x f(x)}{\|\nabla_x f(x)\|_ 2}$$

   In other words, the gradient points directly uphill, and the negative gradient points directly downhill. We can decrease \(f\) by moving in the direction of the negative gradient.

   The method of steepest/gradient descent:
   Proposes a new point to decrease the value of \(f\):

   $$\boldsymbol{x}^{\prime}=\boldsymbol{x}-\epsilon \nabla_{\boldsymbol{x}} f(\boldsymbol{x})$$

   where \(\epsilon\) is the learning rate, defined as:

   $$\epsilon = \dfrac{\delta}{\left\|\nabla_{x} f(x)\right\|_ {2}}$$

   • Derivation Video

   
   

3. The Learning Rate:
   The learning rate is a hyper-parameter that controls how much we are adjusting the weights of our network with respect the loss gradient.

   The learning rate comes from a modification of the step-size in the GD derivation.
   We get the learning rate by employing a simple idea:
   We have a fixed step-size \(\delta\) that dictated how much we should be moving in the direction of steepest descent. However, we would like to keep the step-size from being too small or overshooting. The idea is to make the step-size proportional to the magnitude of the gradient (i.e. some constant multiplied by the magnitude of the gradient):

   $$\delta = \epsilon \left\|\nabla_{x} f(x)\right\|_ {2}$$

   If we do so, we get a nice cancellation as follows:

   $$\begin{aligned}\Delta \boldsymbol{x} &= \delta \hat{\boldsymbol{u}} \\ &= -\delta \dfrac{\nabla_x f(x)}{\|\nabla_x f(x)\|_ 2} \\ &= - \epsilon \left\|\nabla_{x} f(x)\right\|_ {2} \dfrac{\nabla_x f(x)}{\|\nabla_x f(x)\|_ 2} \\ &= - \dfrac{\epsilon \left\|\nabla_{x} f(x)\right\|_ {2}}{\|\nabla_x f(x)\|_ 2} \nabla_x f(x) \\ &= - \epsilon \nabla_x f(x) \end{aligned}$$

   where now we have a fixed learning rate instead of a fixed step-size.

   Choosing the Learning Rate:

   • Set it to a small constant
   • Line Search: evaluate \(f\left(\boldsymbol{x}-\epsilon \nabla_{\boldsymbol{x}} f(\boldsymbol{x})\right)\) for several values of \(\epsilon\) and choose the one that results in the smallest objective value.
     Finds a local minimum along a search direction by solving an optimization problem in 1-D.

     e.g. for smooth \(f\): Secant Method, Newton-Raphson Method (may need Hessian, hard for large dims)
     for non-smooth \(f\): use direct line search e.g. golden section search
     Note: usually NOT used in DL

   • Trust Region Method
   • Grid Search: is simply an exhaustive searching through a manually specified subset of the hyperparameter space of a learning algorithm. It is guided by some performance metric, typically measured by cross-validation on the training set or evaluation on a held-out validation set.
   • Population-Based Training (PBT): is an elegant implementation of using a genetic algorithm for hyper-parameter choice.
     In PBT, a population of models are created. They are all continuously trained in parallel. When any member of the population has had sufficiently long to train to show improvement, its validation accuracy is compared to the rest of the population. If its performance is in the lowest \(20\%\), then it copies and mutates the hyper-parameters and variables of one of the top \(20\%\) performers.
     In this way, the most successful hyper-parameters spawn many slightly mutated variants of themselves and the best hyper-parameters are likely discovered.
   • Bayesian Optimization: is a global optimization method for noisy black-box functions. Applied to hp optimization, it builds a probabilistic model of the function mapping from hp values to the objective evaluated on a validation set. By iteratively evaluating a promising hp configuration based on the current model, and then updating it, it, aims to gather observations revealing as much information as possible about this function and, in particular, the location of the optimum. It tries to balance exploration (hps for which the outcome is most uncertain) and exploitation (hps expected close to the optimum).
     In practice, it has been shown to obtain better results in fewer evaluations compared to grid search and random search, due to the ability to reason about the quality of experiments before they are run.

   Line Search VS Trust Region:
   Trust-region methods are in some sense dual to line-search methods: trust-region methods first choose a step size (the size of the trust region) and then a step direction, while line-search methods first choose a step direction and then a step size.

   Learning Rate Schedule:
   A learning rate schedule changes the learning rate during learning and is most often changed between epochs/iterations. This is mainly done with two parameters: decay and momentum.

   • Decay: serves to settle the learning in a nice place and avoid oscillations, a situation that may arise when a too high constant learning rate makes the learning jump back and forth over a minima, and is controlled by a hyperparameter.
   • Momentum: is analogous to a ball rolling down a hill; we want the ball to settle at the lowest point of the hill (corresponding to the lowest error). Momentum both speeds up the learning (increasing the learning rate) when the error cost gradient is heading in the same direction for a long time and also avoids local minima by ‘rolling over’ small bumps.

   Types of learning rate schedules for Decay:

   • Time-based learning schedules alter the learning rate depending on the learning rate of the previous time iteration. Factoring in the decay the mathematical formula for the learning rate is:

     $${\displaystyle \eta_{n+1}={\frac {\eta_{n}}{1+dn}}}$$

     where \(\eta\) is the learning rate, \(d\) is a decay parameter and \(n\) is the iteration step.

   • Step-based learning schedules changes the learning rate according to some pre defined steps:

     $${\displaystyle \eta_{n}=\eta_{0}d^{floor({\frac {1+n}{r}})}}$$

     where \({\displaystyle \eta_{n}}\) is the learning rate at iteration \(n\), \(\eta_{0}\) is the initial learning rate, \(d\) is how much the learning rate should change at each drop (0.5 corresponds to a halving) and \(r\) corresponds to the droprate, or how often the rate should be dropped (\(10\) corresponds to a drop every \(10\) iterations). The floor function here drops the value of its input to \(0\) for all values smaller than \(1\).

   • Exponential learning schedules are similar to step-based but instead of steps a decreasing exponential function is used. The mathematical formula for factoring in the decay is:

     $$ {\displaystyle \eta_{n}=\eta_{0}e^{-dn}}$$

     where \(d\) is a decay parameter.
     
     

4. Convergence:
   Gradient Descent converges when every element of the gradient is zero, or very close to zero within some threshold.

   With certain assumptions on \(f\) (convex, \(\nabla f\) lipschitz) and particular choices of \(\epsilon\) (chosen via line-search etc.), convergence to a local minimum can be guaranteed.
   Moreover, if \(f\) is convex, all local minima are global minimia, so convergence is to the global minimum.
   
   

5. Choosing (tuning) the hyperparameters:
   We can set/tune most hyperparameters by reasoning about their effect on model capacity.
   Effect of HPs on model capacity

   Important HPs:

   1. Learning Rate
   2. # Hidden Units
   3. Mini-batch Size
   4. Momentum Coefficient

   Hyperparameter search:
   Sample at random in a grid (hypercube) of different parameters, then zoom in to a tighter range of “good” values.
   Search (sample) on a logarithmic scale to get uniform sizes between values:

   • Select value \(r \in [a, b]\) (e.g. \(\in [-4, 0]\), and set your hp as \(10^r\) (e.g. \(\epsilon = 10^{r}\)). You’ll be effectively sampling \(\in [10^{-4}, 10^0] \iff [0.0001, 1]\).
     
     
6. Notes:
   • Gradient descent can be viewed as applying Euler’s method for solving ordinary differential equations \({\displaystyle x'(t)=-\nabla f(x(t))}\) to a gradient flow.
   • Neural nets are unconstrained optimization problems with many, many local minima. They sometimes benefit from line search or second-order optimization algorithms, but when the input data set is very large, researchers often favor the dumb, blind, stochastic versions of gradient descent.
   • Grid search suffers from the curse of dimensionality, but is often embarrassingly parallel because typically the hyperparameter settings it evaluates are independent of each other.
     
     

Gradient Descent Variants

There are three variants of gradient descent, which differ in the amount of data used to compute the gradient. The amount of data imposes a trade-off between the accuracy of the parameter updates and the time it takes to perform the update.

1. Batch Gradient Descent:
   Batch Gradient Descent AKA Vanilla Gradient Descent, computes the gradient of the objective wrt. the parameters \(\theta\) for the entire dataset:

   $$\theta=\theta-\epsilon \cdot \nabla_{\theta} J(\theta)$$

   Since we need to compute the gradient for the entire dataset for each update, this approach can be very slow and is intractable for datasets that can’t fit in memory.
   Moreover, batch-GD doesn’t allow for an online learning approach.
   
   

2. Stochastic Gradient Descent:
   SGD performs a parameter update for each data-point:

   $$\theta=\theta-\epsilon \cdot \nabla_{\theta} J\left(\theta ; x^{(i)} ; y^{(i)}\right)$$

   SGD exhibits a lot of fluctuation and has a lot of variance in the parameter updates. However, although, SGD can potentially move in the wrong direction due to limited information; in-practice, if we slowly decrease the learning-rate, it shows the same convergence behavior as batch gradient descent, almost certainly converging to a local or the global minimum for non-convex and convex optimization respectively.
   Moreover, the fluctuations it exhibits enables it to jump to new and potentially better local minima.

   Notes:

   • Why reduce the learning rate after every epoch?
     This is due to the fact that the random sampling of batches acts as a source of noise which might make SGD keep oscillating around the minima without actually reaching it.
     It is necessary to guarantee convergence.
   • The following conditions guarantee convergence under convexity conditions for SGD:

     $$\begin{array}{l}{\sum_{k=1}^{\infty} \epsilon_{k}=\infty, \quad \text { and }} \\ {\sum_{k=1}^{\infty} \epsilon_{k}^{2}<\infty}\end{array}$$

   • Stochastic Gradient Descent Escapes Saddle Points Efficiently (M.J.)

   
   

3. Mini-batch Gradient Descent:
   A hybrid approach that perform updates for a, pre-specified, mini-batch of \(n\) training examples:

   $$\theta=\theta-\epsilon \cdot \nabla_{\theta} J\left(\theta ; x^{(i : i+n)} ; y^{(i : i+n)}\right)$$

   This allows it to:

   1. Reduce the variance of the parameter updates \(\rightarrow\) more stable convergence
   2. Makes use of matrix-vector highly optimized libraries

Gradient Descent “Optimization”

\(\:\) Evolutionary Map Of Optimizers

1. Challenges in vanilla approaches to gradient descent:
   All the variants described above, however, do not guarantee “good” convergence due to some challenges:
   • Choosing a proper learning rate is usually difficult:
     A learning rate that is too small leads to painfully slow convergence, while a learning rate that is too large can hinder convergence and cause the loss function to fluctuate around the minimum or even to diverge.
   • Learning rate schedules¹ try to adjust the learning rate during training by e.g. annealing, i.e. reducing the learning rate according to a pre-defined schedule or when the change in objective between epochs falls below a threshold. These schedules and thresholds, however, have to be defined in advance and are thus unable to adapt to a dataset’s characteristics².
   • The learning rate is fixed for all parameter updates:
     If our data is sparse and our features have very different frequencies, we might not want to update all of them to the same extent, but perform a larger update for rarely occurring features.
   • Another key challenge of minimizing highly non-convex error functions common for neural networks is avoiding getting trapped in their numerous suboptimal local minima. Dauphin et al.³ argue that the difficulty arises in fact not from local minima but from saddle points, i.e. points where one dimension slopes up and another slopes down. These saddle points are usually surrounded by a plateau of the same error, which makes it notoriously hard for SGD to escape, as the gradient is close to zero in all dimensions.
     
     
2. Preliminaries - Important Concepts:
   Exponentially Weighted Averages:
   EWAs (NG)

   $$v_{t}=\beta v_{t-1}+ (1-\beta) \theta_{t}$$

   You can think of \(v_t\) as approximately averaging over \(\approx \dfrac{1}{1-\beta}\) previous values \(\theta_i\).

   The larger the \(\beta\) the slower \(v_t\) adapts to changes in (new) \(\theta\) and the less noisy the value of \(v_t\).

   Intuition:
   It is a recursive equation. Thus,

   $$v_{100} = (1-\beta) \theta_{100} + (1-\beta)\beta \theta_{99} + (1-\beta)\beta^{2} \theta_{98} + (1-\beta)\beta^{3} \theta_{97} + (1-\beta)\beta^{4} \theta_{96} + \ldots + (1-\beta)\beta^{100} \theta_{1}$$

   • It is an element-wise product between the values of \(\theta_i\) and an exponentially decaying function \(v(i)\).
     For \(T=100, \beta=0.9\):
     
   • The sum of the coefficients of \(\theta_i\) is equal to \(\approx 1\)

     But not exactly \(1\) which is why bias correction is needed.

   • It takes about \((1-\beta)^{\dfrac{1}{\beta}}\) time-steps for \(v\) to decay to about a third of its peak value. So, after \((1-\beta)^{\dfrac{1}{\beta}}\) steps, the weight decays to about a third of the weight of the current time-step \(\theta\) value.
     In general:

     $$(1-\epsilon)^{\dfrac{1}{\epsilon}} \approx \dfrac{1}{e} \approx 0.35 \approx \dfrac{1}{3}$$

     EWAs Intuition (NG)
     
     
     

   Exponentially Weighted Averages Bias Correction:

   The Problem:
   The estimate of the first value \(\theta_1\) will not be a good estimate of because it will be multiplied by \((1-\beta) << 1\). This will be a much lower estimate especially during the initial phase of the estimate. It will produce the purple curve instead of the green curve:
   

   Bias Correction:
   Replace \(v_t\) with:
   \(\:\:\:\:\:\: \dfrac{v_{t}}{1-\beta^{t}}\)

   • Small \(t\): \(\implies \beta^t\) is large \(\implies \dfrac{1}{1-\beta^t}\) is large
   • Large \(t\): \(\implies \beta^t\) is small \(\implies \dfrac{1}{1-\beta^t} \approx 1\)
     
     

3. Momentum:
   Motivation:
   SGD has trouble navigating ravines (i.e. areas where the surface curves much more steeply in one dimension than in another⁴) which are common around local optima.
   In these scenarios, SGD oscillates across the slopes of the ravine while only making hesitant progress along the bottom towards the local optimum.

   Momentum:
   Momentum⁵ is a method that helps accelerate SGD in the relevant direction and dampens oscillations (image^). It does this by adding a fraction \(\gamma\) of the update vector of the past time step to the current update vector:

   $$\begin{aligned} v_{t} &=\gamma v_{t-1}+\eta \nabla_{\theta} J(\theta) \\ \theta &=\theta-v_{t} \end{aligned}$$

   Note: Some implementations exchange the signs in the equations. The momentum term \(\gamma\) is usually set to \(0.9\) or a similar value, and \(v_0 = 0\).

   

   Essentially, when using momentum, we push a ball down a hill. The ball accumulates momentum as it rolls downhill, becoming faster and faster on the way (until it reaches its terminal velocity if there is air resistance, i.e. \(\gamma < 1\)). The same thing happens to our parameter updates: The momentum term increases for dimensions whose gradients point in the same directions and reduces updates for dimensions whose gradients change directions. As a result, we gain faster convergence and reduced oscillation.
   In this case we think of the equation as:

   $$v_{t} =\underbrace{\gamma}_{\text{friction }} \: \underbrace{v_{t-1}}_{\text{velocity}}+\eta \underbrace{\nabla_{\theta} J(\theta)}_ {\text{acceleration}}$$

   Instead of using the gradient to change the position of the weight “particle,” use it to change the velocity. - Hinton

   • Momentum NG

     Momentum Calculation (EWAs):

     $$\begin{align} v_{dw} &= \beta\:v_{dw}+(1-\beta) dw \\ v_{db} &=\beta\:v_{db}+(1-\beta) db \end{align}$$

     Parameter Updates:

     $$\begin{align} w &= w - \epsilon\:v_{dw} \\ b &= b - \epsilon\:v_{d_b} \end{align}$$

   • Why Momentum Really Works (distill)

   Notes:

   • Bias Correction is NOT used in practice; only 10 iterations needed to catch up.
   • The \((1-\beta)\) coefficient usually gets dropped in the literature. The effect is that that lr needs to be rescaled which is not a problem.
   • Learning representations by back-propagating errors (Rumelhart, Hinton)
   • visualizing Momentum (video)
     
     

4. Nesterov Accelerated Gradient:
   Motivation:
   Momentum is good, however, a ball that rolls down a hill, blindly following the slope, is highly unsatisfactory. We’d like to have a smarter ball, a ball that has a notion of where it is going so that it knows to slow down before the hill slopes up again.

   Nesterov Accelerated Gradient (NAG):
   NAG⁶ is a way to five our momentum term this kind of prescience. Since we know that we will use the momentum term \(\gamma\:v_{t-1}\) to move the parameters \(\theta\), we can compute a rough approximation of the next position of the parameters with \(\theta - \gamma v_{t-1}\) (w/o the gradient). This allows us to, effectively, look ahead by calculating the gradient not wrt. our current parameters \(\theta\) but wrt. the approximate future position of our parameters:

   $$\begin{aligned} v_{t} &=\gamma v_{t-1}+\eta \nabla_{\theta} J\left(\theta-\gamma v_{t-1}\right) \\ \theta &=\theta-v_{t} \end{aligned}$$

   \(\gamma = 0.9\),

   While Momentum first computes the current gradient (small blue vector) and then takes a big jump in the direction of the updated accumulated gradient (big blue vector), NAG first makes a big jump in the direction of the previous accumulated gradient (brown vector), measures the gradient and then makes a correction (red vector), which results in the complete NAG update (green vector). This anticipatory update prevents us from going too fast and results in increased responsiveness, which has significantly increased the performance of RNNs on a number of tasks⁷.
   

   Notes:

   • This really helps the optimization of recurrent neural networks⁸
   • Momentum allows us to adapt our updates to the slope of our error function and speed up SGD
   • A Dynamical Systems Perspective on Nesterov Acceleration (M.Jordan)
     
     
5. Adagrad:
   Motivation:
   Now that we are able to adapt our updates to the slope of our error function and speed up SGD in turn, we would also like to adapt our updates to each individual parameter to perform larger or smaller updates depending on their importance.

   The magnitude of the gradient can be very different for different weights and can change during learning: This makes it hard to choose single global learning rate. - Hinton

   Adagrad:
   Adagrad⁹ is an algorithm for gradient-based optimization that does just this: It adapts the learning rate to the parameters, performing smaller updates (i.e. low learning rates) for parameters associated with frequently occurring features, and larger updates (i.e. high learning rates) for parameters associated with infrequent features.

   Adagrad per-parameter update:
   Adagrad uses a different learning rate for every parameter \(\theta_i\) at every time step \(t\), so, we first show Adagrad’s per-parameter update.

   The SGD update for every parameter \(\theta_i\) at each time step \(t\) is:

   $$\theta_{t+1, i}=\theta_{t, i}-\eta \cdot g_{t, i}$$

   where \(g_{t, i}=\nabla_{\theta} J\left(\theta_{t, i}\right)\), is the partial derivative of the objective function w.r.t. to the parameter \(\theta_i\) at time step \(t\), and \(g_{t}\) is the gradient at time-step \(t\).

   In its update rule, Adagrad modifies the general learning rate \(\eta\) at each time step \(t\) for every parameter \(\theta_i\) based on the past gradients that have been computed for \(\theta_i\):

   $$\theta_{t+1, i}=\theta_{t, i}-\frac{\eta}{\sqrt{G_{t, i i}+\epsilon}} \cdot g_{t, i}$$

   \(G_t \in \mathbb{R}^{d \times d}\) here is a diagonal matrix where each diagonal element \(i, i\) is the sum of the squares of the gradients wrt \(\theta_i\) up to time step \(t\)¹⁰, while \(\epsilon\) is a smoothing term that avoids division by zero (\(\approx 1e - 8\)).

   Without the sqrt, the algorithm performs much worse

   As \(G_t\) contains the sum of the squares of the past gradients w.r.t. to all parameters \(\theta\) along its diagonal, we can now vectorize our implementation by performing a matrix-vector product \(\odot\) between \(G_t\) and \(g_t\):

   $$\theta_{t+1}=\theta_{t}-\frac{\eta}{\sqrt{G_{t}+\epsilon}} \odot g_{t}$$

   Properties:

   • Well-suited for dealing with sparse data (because it adapts the lr of each parameter wrt feature frequency)
     • Pennington et al.¹¹ used Adagrad to train GloVe word embeddings, as infrequent words require much larger updates than frequent ones.
   • Eliminates need for manual tuning of lr:
     One of Adagrad’s main benefits is that it eliminates the need to manually tune the learning rate. Most implementations use a default value of \(0.01\) and leave it at that.
   • Weakness -> Accumulation of the squared gradients in the denominator:
     Since every added term is positive, the accumulated sum keeps growing during training. This in turn causes the learning rate to shrink and eventually become infinitesimally small, at which point the algorithm is no longer able to acquire additional knowledge.
   • Visualization - How adaptive gradient methods speedup convergence
     
     

6. Adadelta:
   Motivation:
   Adagrad has a weakness where it suffers from aggressive, monotonically decreasing lr by accumulation of the squared gradients in the denominator. The following algorithm aims to resolve this flow.

   Adadelta:
   Adadelta¹² is an extension of Adagrad that seeks to reduce its aggressive, monotonically decreasing learning rate. Instead of accumulating all past squared gradients, Adadelta restricts the window of accumulated past gradients to some fixed size \(w\).

   Instead of inefficiently storing \(w\) previous squared gradients, the sum of gradients is recursively defined as a decaying average of all past squared gradients. The running average \(E\left[g^{2}\right]_ {t}\) at time step \(t\) then depends (as a fraction \(\gamma\) similarly to the Momentum term) only on the previous average and the current gradient:

   $$E\left[g^{2}\right]_{t}=\gamma E\left[g^{2}\right]_{t-1}+(1-\gamma) g_{t}^{2}$$

   We set \(\gamma\) to a similar value as the momentum term, around \(0.9\).
   For clarity, we now rewrite our vanilla SGD update in terms of the parameter update vector \(\Delta \theta_{t}\):

   $$\begin{aligned} \Delta \theta_{t} &=-\eta \cdot g_{t, i} \\ \theta_{t+1} &=\theta_{t}+\Delta \theta_{t} \end{aligned}$$

   In the parameter update vector of Adagrad, we replace the diagonal matrix \(G_t\) with the decaying average over past squared gradients \(E[g^2]_ t\):

   $$-\frac{\eta}{\sqrt{E[g^2]_ t+\epsilon}} \odot g_{t}$$

   Since the denominator is just the root mean squared (RMS) error criterion of the gradient, we can replace it with the criterion short-hand:

   $$-\frac{\eta}{RMS[g]_{t}} \odot g_{t}$$

   This modified parameter update vector does NOT have the same hypothetical units as the parameter.
   We accomplish this by first defining another exponentially decaying average, this time not of squared gradients but of squared parameter updates:

   $$E[\Delta \theta^2]_t = \gamma E[\Delta \theta^2]_{t-1} + (1 - \gamma) \Delta \theta^2_t$$

   The RMS Error of parameter updates is thus:

   $$RMS[\Delta \theta]_ {t} = \sqrt{E[\Delta \theta^2]_ t + \epsilon}$$

   Since \(RMS[\Delta \theta]_ {t}\) is unknown, we approximate it with the \(RMS\) of parameter updates up to (until) the previous time step. Replacing the learning rate \(\eta\) in the previous update rule with \(RMS[\Delta \theta]_ {t-1}\) finally yields the Adadelta update rule:

   $$\begin{align} \begin{split} \Delta \theta_t &= - \dfrac{RMS[\Delta \theta]_{t-1}}{RMS[g]_{t}} g_{t} \\ \theta_{t+1} &= \theta_t + \Delta \theta_t \end{split} \end{align}$$

   
   

   Properties:

   • Eliminates need for lr completely:
     With Adadelta, we do not even need to set a default learning rate, as it has been eliminated from the update rule.
     
     

7. RMSprop:
   Motivation:
   RMSprop and Adadelta have both been developed independently around the same time stemming from the need to resolve Adagrad’s radically diminishing learning rates.

   RMSprop:
   RMSprop is an unpublished, adaptive learning rate method proposed by Geoff Hinton in Lecture 6e of his Coursera Class.

   RMSprop in fact is identical to the first update vector of Adadelta that we derived above:

   $$\begin{align} \begin{split} E[g^2]_t &= 0.9 E[g^2]_{t-1} + 0.1 g^2_t \\ \theta_{t+1} &= \theta_{t} - \dfrac{\eta}{\sqrt{E[g^2]_t + \epsilon}} g_{t} \end{split} \end{align}$$

   RMSprop as well divides the learning rate by an exponentially decaying average of squared gradients.
   Hinton suggests \(\gamma\) to be set to \(0.9\), while a good default value for the learning rate \(\eta\) is \(0.001\).

   RMSprop as an extension of Rprop:
   Hinton, actually, thought of RMSprop as a way of extending Rprop to work with mini-batches.
   Why Rprop does not work with mini-batches?

   Rprop: is equivalent to using the gradient but also dividing by the magnitude of the gradient.
   The problem with mini-batch rprop is that we divide by a different number for each mini-batch.
   So why not force the number we divide by to be very similar for adjacent mini-batches?
   That is the idea behind RMSprop.
   
   

   Notes:

   • It is of note that Hinton has tried to add momentum to RMSprop and found that “it does not help as much as it normally does - needs more investigation”.
   • Visualizing Rprop - How adaptive gradient methods speedup convergence
     
     

8. Adam:
   Motivation:
   Adding momentum to Adadelta/RMSprop.

   Adam:
   Adaptive Moment Estimation (Adam)¹³ is another method that computes adaptive learning rates for each parameter. In addition to storing an exponentially decaying average of past squared gradients \(v_t\) like Adadelta and RMSprop, Adam also keeps an exponentially decaying average of past gradients \(m_t\), similar to momentum.

   Adam VS Momentum:
   Whereas momentum can be seen as a ball running down a slope, Adam behaves like a heavy ball with friction, which thus prefers flat minima in the error surface[^15].

   We compute the decaying averages of past and past squared gradients \(m_t\) and \(v_t\) respectively as follows:

   $$\begin{align} \begin{split} m_t &= \beta_1 m_{t-1} + (1 - \beta_1) g_t \\ v_t &= \beta_2 v_{t-1} + (1 - \beta_2) g_t^2 \end{split} \end{align}$$

   \(m_t\) and \(v_t\) are estimates of the first moment (the mean) and the second moment (the uncentered variance) of the gradients respectively, hence the name of the method.
   As \(m_t\) and \(v_t\) are initialized as vectors of \(0\)’s, the authors of Adam observe that they are biased towards zero, especially during the initial time steps, and especially when the decay rates are small (i.e. \(\beta_1\) and \(\beta_2\) are close to \(1\)).

   They counteract these biases by computing bias-corrected first and second moment estimates:

   $$\begin{align} \begin{split} \hat{m}_ t &= \dfrac{m_t}{1 - \beta^t_1} \\ \hat{v}_ t &= \dfrac{v_t}{1 - \beta^t_2} \end{split} \end{align}$$

   They then use these to update the parameters just as we have seen in Adadelta and RMSprop, which yields the Adam update rule:

   $$\theta_{t+1} = \theta_{t} - \dfrac{\eta}{\sqrt{\hat{v}_ t} + \epsilon} \hat{m}_ t$$

   The authors propose default values of \(0.9\) for \(\beta_1\), \(0.999\) for \(\beta_2\), and \(10^{ −8}\) for \(\epsilon\). They show empirically that Adam works well in practice and compares favorably to other adaptive learning-method algorithms.
   
   

9. AdaMax

10. Nadam

11. AMSGrad:
    Motivation:
    Adaptive LR methods fail to converge to an optimal solution in some cases, e.g. for object recognition [17] or machine translation [18].
    Reddi et al. (2018) [19] formalize this issue and pinpoint the exponential moving average of past squared gradients as a reason for the poor generalization behaviour of adaptive learning rate methods.

    In settings where Adam converges to a suboptimal solution, it has been observed that some minibatches provide large and informative gradients, but as these minibatches only occur rarely, exponential averaging diminishes their influence, which leads to poor convergence.
    To fix this behaviour, the authors propose a new algorithm, AMSGrad that uses the maximum of past squared gradients \(v_t\) rather than the exponential average to update the parameters.

    Instead of using \(v_{t}\) (or its bias-corrected version \(\hat{v}_{t}\)) directly, we now employ the previous \(v_{t-1}\) if it is larger than the current one:
    \(\hat{v}_{t}=\max \left(\hat{v}_{t-1}, v_{t}\right)\)

    This way, AMSGrad results in a non-increasing step size, which avoids the problems suffered by Adam. For simplicity, the authors also remove the debiasing step that we have seen in Adam.

    Parameter Updates:

    $$ \begin{aligned} m_{t} &=\beta_{1} m_{t-1}+\left(1-\beta_{1}\right) g_{t} \\ v_{t} &=\beta_{2} v_{t-1}+\left(1-\beta_{2}\right) g_{t}^{2} \\ \hat{v}_{t} &=\max \left(\hat{v}_{t-1}, v_{t}\right) \\ \theta_{t+1} &=\theta_{t}-\frac{\eta}{\sqrt{\hat{v}_{t}}+\epsilon} m_{t} \end{aligned} $$

    TLDR: AMSGrad = Adam but always divide by max \(\hat{v}_ i\) for \(i \in [1, t]\).
    
    

12. Visualization of the Algorithms
    SGD optimization on loss surface contours:
    

    We see their behavior on the contours of a loss surface (the Beale function) over time. Note that Adagrad, Adadelta, and RMSprop almost immediately head off in the right direction and converge similarly fast, while Momentum and NAG are led off-track, evoking the image of a ball rolling down the hill. NAG, however, is quickly able to correct its course due to its increased responsiveness by looking ahead and heads to the minimum.

    
    

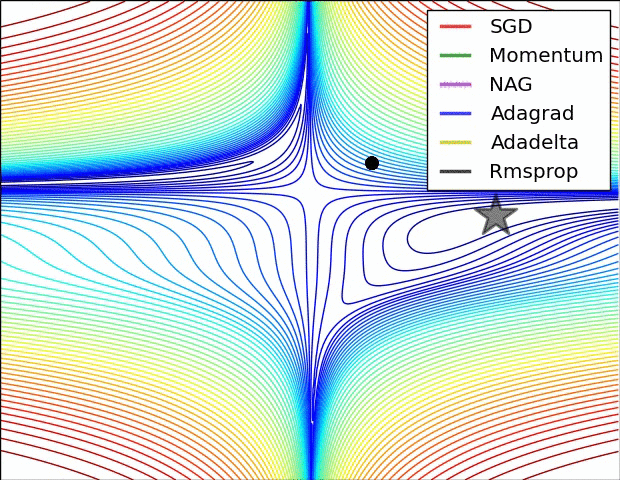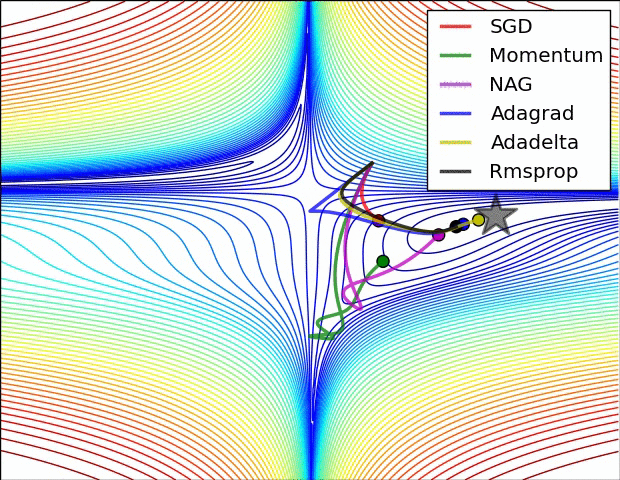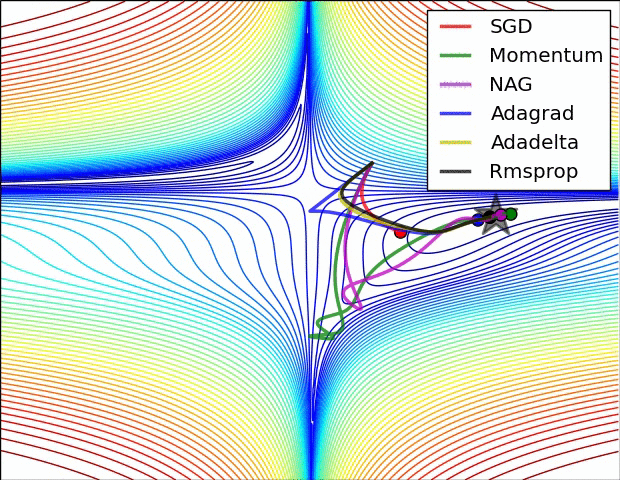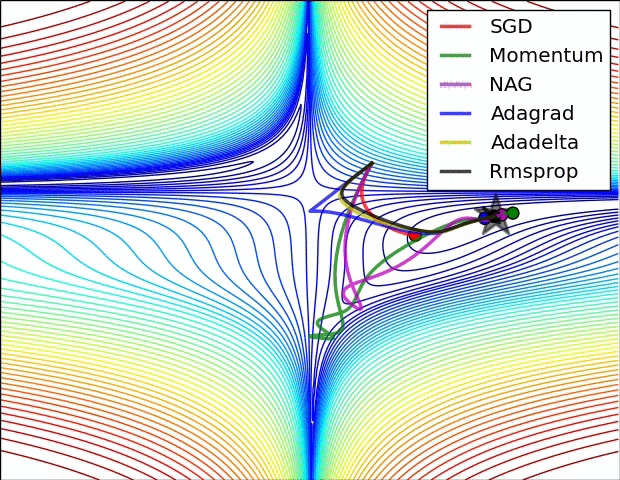
    SGD optimization on saddle point:
    

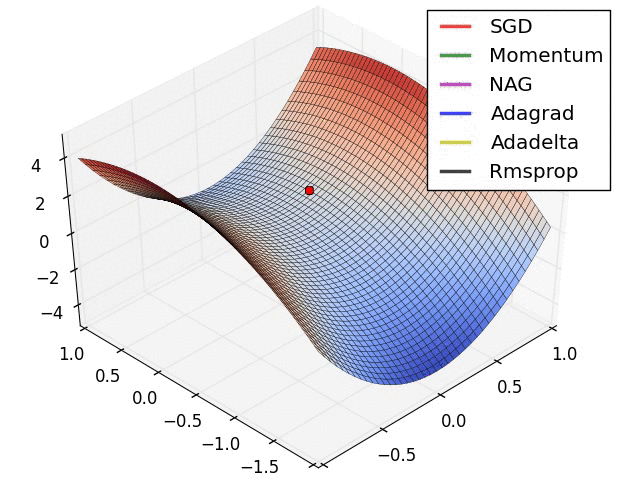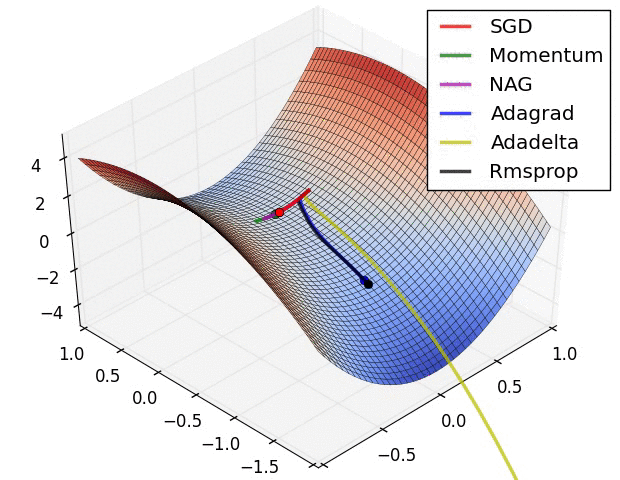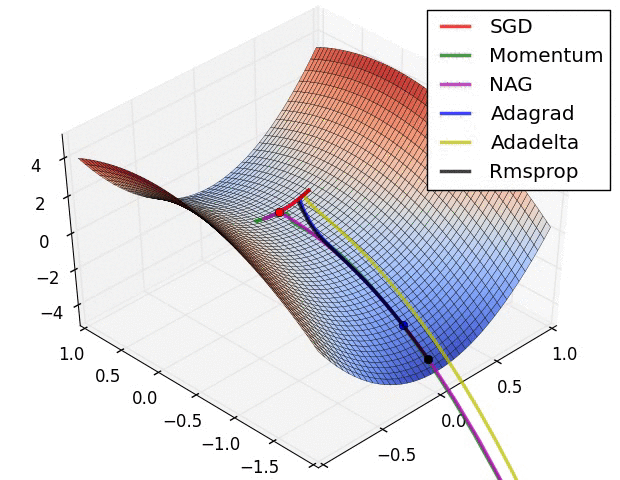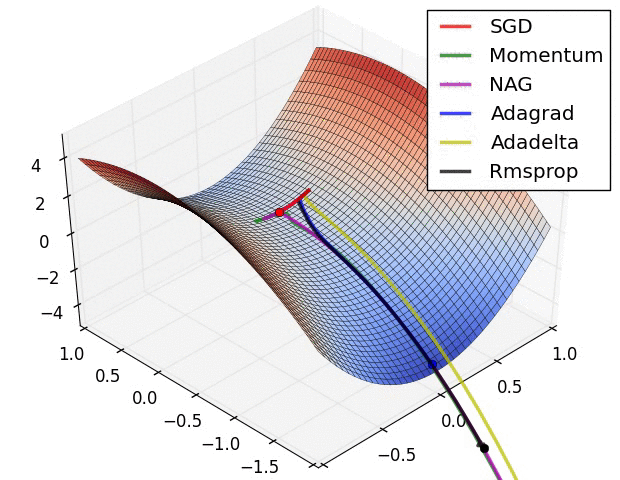
    Image shows the behavior of the algorithms at a saddle point, i.e. a point where one dimension has a positive slope, while the other dimension has a negative slope, which pose a difficulty for SGD as we mentioned before. Notice here that SGD, Momentum, and NAG find it difficulty to break symmetry, although the two latter eventually manage to escape the saddle point, while Adagrad, RMSprop, and Adadelta quickly head down the negative slope.

    Analysis:
    As we can see, the adaptive learning-rate methods, i.e. Adagrad, Adadelta, RMSprop, and Adam are most suitable and provide the best convergence for these scenarios.

    Tutorial for Visualization

13. Analysis - Choosing an Optimizer:
    • Sparse Input Data:
      If your input data is sparse, then you likely achieve the best results using one of the adaptive learning-rate methods. An additional benefit is that you won’t need to tune the learning rate but likely achieve the best results with the default value.

    In summary, RMSprop is an extension of Adagrad that deals with its radically diminishing learning rates. It is identical to Adadelta, except that Adadelta uses the RMS of parameter updates in the numerator update rule. Adam, finally, adds bias-correction and momentum to RMSprop. Insofar, RMSprop, Adadelta, and Adam are very similar algorithms that do well in similar circumstances. Kingma et al.¹³ show that its bias-correction helps Adam slightly outperform RMSprop towards the end of optimization as gradients become sparser. Insofar, Adam might be the best overall choice.

    Interestingly, many recent papers use vanilla SGD without momentum and a simple learning rate annealing schedule. As has been shown, SGD usually achieves to find a minimum, but it might take significantly longer than with some of the optimizers, is much more reliant on a robust initialization and annealing schedule, and may get stuck in saddle points rather than local minima. Consequently, if you care about fast convergence and train a deep or complex neural network, you should choose one of the adaptive learning rate methods.

Parallelizing and distributing SGD

Additional strategies for optimizing SGD

For a great overview of some other common tricks, refer to¹⁴

1. Shuffling and Curriculum Learning:
   Generally, we want to avoid providing the training examples in a meaningful order to our model as this may bias the optimization algorithm. Consequently, it is often a good idea to shuffle the training data after every epoch.

   On the other hand, for some cases where we aim to solve progressively harder problems, supplying the training examples in a meaningful order may actually lead to improved performance and better convergence. The method for establishing this meaningful order is called Curriculum Learning¹⁵.

   Zaremba and Sutskever¹⁶ were only able to train LSTMs to evaluate simple programs using Curriculum Learning and show that a combined or mixed strategy is better than the naive one, which sorts examples by increasing difficulty.

   Note: “Generally, we want to avoid providing the training examples in a meaningful order to our model as this may bias the optimization algorithm.”
   Yes, ok, but this is just the kind of bias that we want to introduce to the network.

   
   

2. Batch Normalization:
   To facilitate learning, we typically normalize the initial values of our parameters by initializing them with zero mean and unit variance. As training progresses and we update parameters to different extents, we lose this normalization, which slows down training and amplifies changes as the network becomes deeper.

   Batch normalization¹⁷ reestablishes these normalizations for every mini-batch and changes are back-propagated through the operation as well. By making normalization part of the model architecture, we are able to use higher learning rates and pay less attention to the initialization parameters. Batch normalization additionally acts as a regularizer, reducing (and sometimes even eliminating) the need for Dropout.

   Goodfellow on BN
   Excellent Blog on BN
   
   

3. Early Stopping:
   According to Geoff Hinton: “Early stopping (is) beautiful free lunch” (NIPS 2015 Tutorial slides, slide 63). You should thus always monitor error on a validation set during training and stop (with some patience) if your validation error does not improve enough.
   
   

4. Gradient Noise:
   Neelakantan et al.¹⁸ add noise that follows a Gaussian distribution \(\mathcal{N}(0, \sigma^2_t)\) to each gradient update:

   $$g_{t, i} = g_{t, i} + \mathcal{N}(0, \sigma^2_t)$$

   They anneal the variance according to the following schedule:

   $$\sigma^2_t = \dfrac{\eta}{(1 + t)^\gamma}$$

   They show that adding this noise makes networks more robust to poor initialization and helps training particularly deep and complex networks. They suspect that the added noise gives the model more chances to escape and find new local minima, which are more frequent for deeper models.

Further Advances in DL Optimization