Table of Contents

Deeper Understanding of Batch Normalization
Preprocessing for Deep Learning
Self Normalizing Neural Networks
An Overview of Normalization Methods in Deep Learning

img

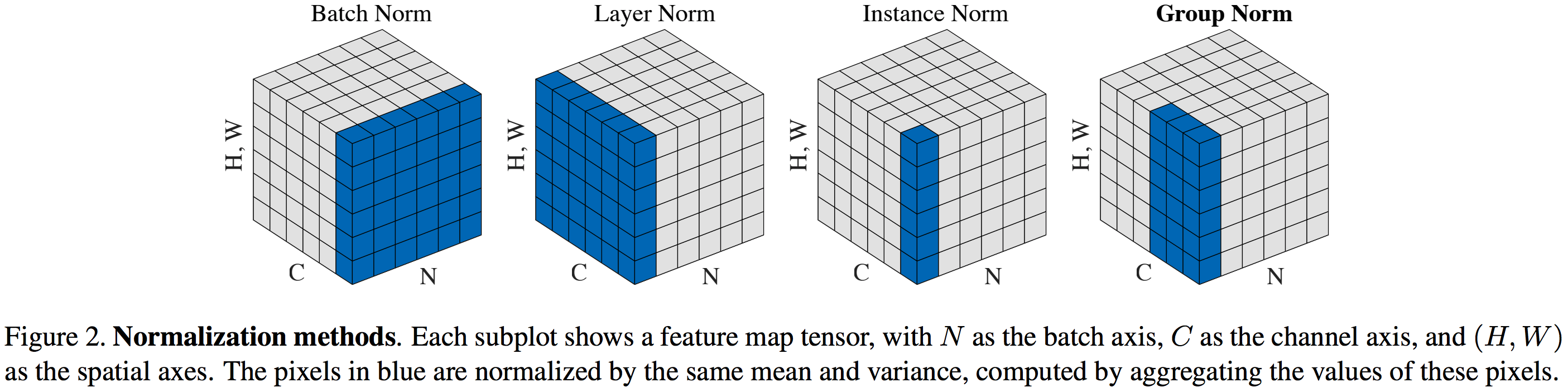
Normalization

  1. Normalization:
    Normalization, aka Feature Scaling, is a method used to normalize the range of independent variables or features of data. It is generally performed during the data preprocessing step.

    Motivation:
    Since the range of values of raw data varies widely, in some machine learning algorithms, objective functions will not work properly without normalization (e.g. dot-product-based functions are scale sensitive).
    Moreover, normalizing the inputs leads to spherical contours of the objective which makes the optimization easier (for vanilla sgd) and speeds up the convergence.


  2. Input Normalization:

    Rescaling (min-max normalization):
    is the simplest method and consists in rescaling the range of features to scale the range in \([0, 1]\) or \([−1, 1]\). Selecting the target range depends on the nature of the data. To rescale to \([0, 1]\) range:

    $$x'=\dfrac{x-{\text{min}}(x)}{ {\text{max}}(x)-{\text{min}}(x)}$$

    To rescale a range between an arbitrary set of values \([a, b]\), the formula becomes:

    $${\displaystyle x'=a+{\frac {(x-{\text{min}}(x))(b-a)}{ {\text{max}}(x)-{\text{min}}(x)}}}$$

    where \(a,\: b\) are the min-max values.

    (Zero-) Centering - Mean Normalization:

    • Define the mean \(\mu_j\) of each feature of the datapoints \(x^{(i)}\):

      $$\mu_{j}=\frac{1}{m} \sum_{i=1}^{m} x_{j}^{(i)}$$

    • Replace each \(x_j^{(i)}\) with \(x_j - \mu_j\)

    Standardization (Z-score Normalization):
    Feature standardization makes the values of each feature in the data have zero-mean (when subtracting the mean in the numerator) and unit-variance. Subtract the mean from each feature, then, divide the values of each feature by its standard deviation.

    $$x' = \frac{x - \bar{x}}{\sigma}$$

    (Scaling to) Unit Length Normalization:
    Another option that is widely used in machine-learning is to scale the components of a feature vector such that the complete vector has length one. This usually means dividing each component by the Euclidean length of the vector:

    $${\displaystyle x'={\frac {x}{\left\|{x}\right\|}}}$$

    We can use \(L_1\) norm or other metrics based on problem.


  3. Activation Normalization:
    Extends the idea of input normalization to deeper networks. Interprets activations in a layer as a featurized input (abstract representation of the input) and aims to normalize those layer outputs/activations.

    The difference however, is in the target mean and variance we want to achieve. Unlike inputs, we might not want to force the activations to have mean\(=0\) and variance\(=1\). E.g. if we are using the sigmoid activation; mean\(=0\) and variance\(=1\) will utilize the linear part of sigmoid. So, changing the mean and variance will allow the network to take advantage of the non-linearity.
    img

    In practice, it’s much more common to normalize the outputs before applying the activation (e.g. in Batch-Norm)


  4. Statistical Normalization - Transformations:
    Let \(X\) be \(n \times d\) design matrix of sample pts.
    Each row \(i\) of \(X\) is a sample pt \(X_i^T\).

    Centering Transform:
    AKA Mean Normalization is just removing the mean from each observation. It centers the data around \(0\).

    $$X' = X - \mathbf{\mu}$$

    where \(\mathbf{\mu}\) is the mean of all the rows of \(X\).

    Decorrelation Transform:
    removes only the correlations but leaves variances intact,

    $$Z = X'V$$

    where \(\text{Var}(X') = \Sigma = \dfrac{1}{n}X'^TX' = V\Lambda V^T\), and \(\text{Var}(Z) = \Lambda\) is the sample covariance matrix.

    It transforms the sample points to the eigenvector coordinate system.

    Standardization Transform:
    sets variances to \(1\) but leaves correlations intact,

    $$X'_s = \dfrac{X - \mathbf{\mu}}{\mathbf{\sigma}_ X}$$

    where \(\mathbf{\sigma}_ X\) is the standard deviation of all the rows of \(X\).

    Sphering Transform:
    Rescales the uncorrelated matrix \(Z\) in order to obtain a covariance matrix corresponding to the identity matrix. To do that we scale our decorrelated data by dividing each dimension by the square-root of its corresponding eigenvalue.

    $$W = X'\Sigma^{-1/2} = X'(V \Lambda^{-1/2} V^T)$$

    this is ZCA whitening.

    Whitening Transform:
    The Whitening Transformation is a linear transformation that transforms a vector of random variables with a known covariance matrix into a set of new variables whose covariance is the identity matrix, meaning that they are uncorrelated and each have variance 1. The transformation is called “whitening” because it changes the input vector into a white noise vector.
    = Centering + Sphering

    Then \(W\) has covariance matrix \(I . \left[\text { If } X_{i} \sim \mathcal{N}(\mu, \Sigma), \text { then approximately, } W_{i} \sim \mathcal{N}(0, I)\right]\).

    Notes:

    • Decorrelation: intuitively, it means that we want to rotate the data until there is no correlation anymore.
    • Centering seems to make it easier for hidden units to get into a good operating region of the sigmoid or ReLU
    • Standardization (normalizing variance) makes the objective function better conditioned, so gradient descent converges faster


Batch Normalization

  1. Batch Normalization:
    Batch Normalization is a normalization method that normalizes activations in a network across the mini-batch. For each feature, batch normalization computes the mean and variance of that feature in the mini-batch. It then subtracts the mean and divides the feature by its mini-batch standard deviation.
    This restricts the activations to have \(0\) mean and unit variance.
    This is followed by an affine transformation of the normalized activations to rescale the mean and variance, in a learnable way, to whatever the network sees fit. This is done because restricting the mean and variance of the activations might hinder the network from taking advantage of the freedom of setting the distribution of the activations to something that might help the later layers learn faster. This means that the expressiveness of the network does not change.

    Notes:

    • Scale Invariance: Batch Norm renders the loss function of neural networks scale invariant.
      I.E. scaling the weights by a constant does not change the output, or the loss, of the batch normalized network.
      • Implications of Scale Invariance - Exponentially Growing Learning Rate:
        • It is possible to use exponentially growing learning rate schedule when training neural networks with batch normalization.
        • The paper establishes the following Equivalence:
          • Weight decay with constant learning rate
          • No weight decay and an exponentially growing learning rate

          This equivalence holds for other normalization layers as well, Group Normalization, Layer Normalization, Instance Norm, etc.

    • Weight Decay and BN:
      • This Paper shows that weight decay on a BN-network is just tweaking the effective learning rate.
      • Without weight decay, the gradient of a BN-network is always orthogonal to the current value of the parameter vector and therefore increases the scale of weights (reduces effective learning rate).
        Intuitively, you can compensate the decrease of effective learning rate by using an exponential learning rate scheme or just simply weight decay.

  2. Effectiveness of Batch Normalization:
    There are many different proposed reasons that try to explain the wide success and effectiveness of the method. We summarize here some of those reasons and give an intuition to why those reasons apply.

    Summarizing the intuition of why BN works:
    The overall intuition is that batch normalization makes the loss surface “easier to navigate”, making optimization easier, enabling the use of higher learning rates, and improving model performance across multiple tasks.
    Further, there is a regularization effect when using BN induced by added noise to the estimate of the mean and variance of the data due to using mini-batches instead.


  3. Internal Covariate Shift as an Intuitive but Wrong Motivation for the Success of BN:
    The correlation between batch normalization and internal covariate shift is widely accepted but was not supported by experimental results. Scholars recently show with experiments that the hypothesized relationship is not an accurate one. Rather, the enhanced accuracy with the batch normalization layer seems to be independent of internal covariate shift.

    Two Problems with the ICS Explanation:

    1. Even if the mean and variance are constant, the distribution of activations can still change. Why are the mean and variance so important?
    2. If we introduce \(\gamma\) and \(\beta\), the mean and variance will deviate from \(0\) and \(1\) anyway. What then, is the point of batch normalization?

  4. Suppressing Higher-Order Effects (Goodfellow):

    Quick Intuition:

    • In a neural network, changing one weight affects subsequent layers, which then affect subsequent layers, and so on.
    • This means changing one weight can make the activations fly all over the place in complex ways.
    • This forces us to use lower learning rates to prevent the gradients from exploding, or – if we use sigmoid activations – to prevent the gradients from disappearing.
    • Batch normalization to the rescue! Batch normalization reparameterizes the network to make optimization easier.
    • With batch normalization, we can control the magnitude and mean of the activations independent of all other layers.
    • This means weights don’t fly all over the place (as long as we have sensible initial means and magnitudes), and we can optimize much easier.

    Further Intuition:
    Deep Neural networks have higher-order interactions, which means changing weights of one layer might also affect the statistics of other layers in addition to the loss function. These cross layer interactions, when unaccounted lead to internal covariate shift. Every time we update the weights of a layer, there is a chance that it affects the statistics of a layer further in the neural network in an unfavorable way.
    Convergence may require careful initializing, hyperparameter tuning and longer training durations in such cases. However, when we add the batch normalized layer between the layers, the statistics of a layer are only affected by the two hyperparameters \(\gamma\) and \(\beta\). Now our optimization algorithm has to adjust only two hyperparameters to control the statistics of any layer, rather than the entire weights in the previous layer. This greatly speeds up convergence, and avoids the need for careful initialization and hyperparameter tuning. Therefore, Batch Norm acts more like a check pointing mechanism.

    Notice that the ability to arbitrarily set the mean and the standard deviation of a layer also means that we can recover the original distribution if that was sufficient for proper training.


  5. Induced Smoothness of the Optimization Landscape (Santurkar et al.):
    In a new paper, the authors claim that BN works because it makes the loss surface smoother. Concretely, it improves the \(\beta\)-smoothness or the Lipschitzness of the function. This smoothness induces a more predictive and stable behavior of the gradients, allowing for faster training.


  6. Batch Norm as a Regularizer:
    BN also acts a regularizer. The mean and the variance estimated for each batch is a noisier version of the true mean, and this injects randomness in our optima search. This helps in regularization.

  7. Length-Direction Decoupling:
    It is argued that the success of batch normalization could be at least partially credited to the length-direction decoupling effect that the method provides.

    By interpreting the batch normalization procedure as the reparametrization of weight space, it could be shown that the length and the direction of the weights are separated after the procedure, and they could thus be trained separately.

    This property could then be used to prove the faster convergence of problems with batch normalization:

  8. Limitations/Problems of BN:

    When doing normalization, we ideally want to the use the global mean and variance to standardize our data. Computing this for each layer is far too expensive though, so we need to approximate using some other measures. BN approximates the mean and variance with those of the mini batch, which is a noisy estimate. Although, we motivated some of the effectiveness of BN to its regularizing effects due to this, same, noisy estimate, this estimate can be problematic in the following scenarios:

    1. Small Batch Sizes:
      If the batch size is \(1\), the variance is \(0\) so batch normalization cannot be applied. Slightly larger mini-batch sizes won’t have this problem, but small mini-batches make our estimates very noisy and can negatively impact training, meaning batch normalization imposes a certain lower bound on our batch size.
    2. Recurrent Connections in an RNN:
      In an RNN, the recurrent activations of each time-step will have different statistics. This means that we have to fit a separate batch normalization layer for each time-step. This makes the model more complicated and – more importantly – it forces us to store the statistics for each time-step during training.
    3. Dependence of the loss between samples in a mini-batch:
      BN makes the loss value for each sample in a mini-batch dependent on other samples in the mini-batch. For instance, if a sample causes a certain layer’s activations to become much larger, this will make the mean and variance larger as well. This will change the activation for all other samples in the mini-batch as well. Furthermore, the mini-batch statistics will depend on the mini-batch size as well (a smaller mini-batch size will increase the random variation in the mean and variance statistics). The problem arises not when training a model on a single machine, but when we start to conduct distributed training, things can get ugly. As mentioned in this paper, we need to take extra care in choosing the batch size and learning rate in the presence of batch normalization when doing distributed training. If two different machines use different batch sizes, they will indirectly be optimizing different loss functions: this means that the value of \(\gamma\) that worked for one machine is unlikely to work for another machine. This is why the authors stressed that the batch size for each worker must be kept constant across all machines.
    4. BN parameters in Fine-Tuning Applications:
      When Fine-Tuning a larger network by freezing all the layers except the last layer; it is unclear if one should use the mean and variance computed on the original dataset or use the mean and variance of the mini-batches. Though most frameworks use the mini-batch statistics, if we are using a different mini-batch size there will be a mismatch between the optimal batch normalization parameters and the parameters in the network.
      If there is a mis-match in the mini-batch sizes it seems to be better to use the statistics of the original dataset instead.
      Further Discussion


Weight Normalization

  1. Weight Normalization:
    Weight Normalization is a normalization method that, instead of normalizing the mini-batch, normalizes the weights of the layer.

    WN reparameterizes the weights \(\boldsymbol{w}\) of any layer in the network in the following way:

    $$\boldsymbol{w}=\frac{g}{\|\boldsymbol{v}\|} \boldsymbol{v} \:\:\:\:\:\:\: $$

    where \(\boldsymbol{v}\) is a \(k\)-dimensional vector, \(g\) is a scalar, and \(\|\boldsymbol{v}\|\) denotes the Euclidean norm of \(\boldsymbol{v}\).
    This reparameterization has the effect of fixing the Euclidean norm of the weight vector \(\boldsymbol{w}\): we now have \(\|\boldsymbol{w}\| = g\), independent of the parameters \(\boldsymbol{v}\).

    Weight Normalization separates the norm of the weight vector from its direction without reducing expressiveness:

    • For variance, this has a similar effect to dividing the inputs by the standard deviation in batch normalization.
    • As for the mean, the authors of the paper proposed using a method called “mean-only batch normalization” together with weight normalization.

  2. Advantages:
    • Since WN separates the norm of the weight vector from its direction, and then optimizes both \(g\) and \(\boldsymbol{v}\) using gradient descent. This change in learning dynamics makes optimization easier.
    • It makes the mean and variance independent of the batch; since now they are connected to the weights of the network.
    • It is often much faster than BN. In CNNs, the number of weights tends to be far smaller than the number of inputs, meaning weight normalization is computationally cheaper compared to batch normalization (CNNs share weights).

  3. Mean-Only Batch Normalization:
    Although weight normalization on its own can assist training, the authors of the paper proposed using a method called “mean-only batch normalization” in conjunction with weight normalization.

    Mean-Only Batch Normalization is a method that subtracts out the mean of the mini-batch but does not divide the inputs by the standard deviation or rescales them.

    Though this method counteracts some of the computational speed-up of weight normalization, it is cheaper than batch-normalization since it does not need to compute the standard deviations. The authors claim that this method provides the following benefits:

    1. It makes the mean of the activations independent from \(\boldsymbol{v}\):
      Weight normalization independently cannot isolate the mean of the activations from the weights of the layer, causing high-level dependencies between the means of each layer. Mean-only batch normalization can resolve this problem.
    2. It adds “gentler noise” to the activations:
      One of the side-effects of batch normalization is that it adds some stochastic noise to the activations as a result of using noisy estimates computed on the mini-batches. This has a regularization effect in some applications but can be potentially harmful in some noise-sensitive domains like reinforcement learning. The noise caused by the mean estimations, however, are “gentler” since the law of large numbers ensures the mean of the activations is approximately normally distributed.
      Thus, weight normalization can still work in settings with a smaller mini-batch size.

Layer Normalization

  1. Layer Normalization:
    Layer Normalization is a normalization method developed by Hinton that, instead of normalizing the inputs across batches like BN, normalizes the inputs across the features:

    $$\begin{aligned} \mu_{i} &=\frac{1}{m} \sum_{j=1}^{m} x_{i j} \\ \sigma_{i}^{2} &=\frac{1}{m} \sum_{j=1}^{m}\left(x_{i j}-\mu_{i}\right)^{2} \\ \hat{x}_{i j} &=\frac{x_{i j}-\mu_{i}}{\sqrt{\sigma_{i}^{2}+\epsilon}} \end{aligned}$$

    This is deceptively similar to the batch norm equations:

    $$\begin{aligned} \mu_{j} &=\frac{1}{m} \sum_{i=1}^{m} x_{i j} \\ \sigma_{j}^{2} &=\frac{1}{m} \sum_{i=1}^{m}\left(x_{i j}-\mu_{j}\right)^{2} \\ \hat{x}_{i j} &=\frac{x_{i j}-\mu_{j}}{\sqrt{\sigma_{j}^{2}+\epsilon}} \end{aligned}$$

    where \(x_{i j}\) is the \(i,j\)-th element of the input, the first dimension represents the batch and the second represents the feature (I have modified the notation from the original papers to make the contrast clearer).


    In batch normalization, the statistics are computed across the batch and are the same for each example in the batch. In contrast, in layer normalization, the statistics are computed across each feature and are independent of other examples.

    This means that layer normalization is not a simple reparameterization of the network, unlike the case of weight normalization and batch normalization, which both have the same expressive power as an unnormalized neural network. The layer normalized model, thus, has different invariance properties than the other methods.

  2. Advantages:
    • The independence between inputs means that each input has a different normalization operation, allowing arbitrary mini-batch sizes to be used.
    • The experimental results show that layer normalization performs well for recurrent neural networks.

  3. Analysis of the Invariance Properties of LN:

Instance Normalization

  1. Instance Normalization:
    Instance Normalization is similar to layer normalization but with an extra restriction: it computes the mean/standard deviation and normalize across each channel in each training example.

    Motivation:
    In Style Transfer problems, the network should be agnostic to the contrast of the original image.
    Therefore, it is specific to images and not trivially extendable to RNNs.

    Experimental results show that instance normalization performs well on style transfer when replacing batch normalization. Recently, instance normalization has also been used as a replacement for batch normalization in GANs.

Group Normalization

  1. Group Normalization:
    Group Normalization computes the mean and standard deviation over groups of channels for each training example.
    You can think of GN as being half way between layer normalization and instance normalization:
    • When we put all the channels into a single group, it becomes Layer Normalization
    • When we put each channel in a different group, it becomes Instance Normalization

  2. Motivation/Advantages:
    Layer Norm and Instance Norm were significantly inferior to BN on image recognition tasks. Group Normalization was able to achieve much closer performance to BN with a batch-size of 32 on ImageNet and outperformed it on smaller batch sizes.

    For tasks like object detection and segmentation that use much higher resolution images (and therefore cannot increase their batch size due to memory constraints), Group Normalization was shown to be a very effective normalization method.

  3. Effectiveness of Group Normalization:

    Why is group normalization so effective compared to layer normalization and instance normalization?

    Layer Norm makes an implicit assumption that all channels are “equally important” when computing the mean. This assumption is often not true in convolution layers.
    For instance, neurons near the edge of an image and neurons near the center of an image will have very different activation statistics. This means that computing different statistics for different channels can give models much-needed flexibility.

    Instance Norm, on the other hand, assumes that the channels are completely independent from each other. Channels in an image are not completely independent though, so being able to leverage the statistics of nearby channels is an advantage group normalization has over instance normalization.

Batch ReNormalization

  1. Batch ReNormalization:
    Batch ReNormalization is an extension of BN for applying batch normalization to small batch sizes.

    In the Authors words: “an effective extension to ensure that the training and inference models generate the same outputs that depend on individual examples rather than the entire mini-batch”

    The authors propose to use a moving average while also taking the effect of previous layers on the statistics into account. Their method is – at its core – a simple reparameterization of normalization with the moving average. If we denote the moving average mean and standard deviation as \(\mu\) and \(\sigma\) and the mini-batch mean and standard deviation as \(\mu_B\) and \(\sigma_B\), the batch renormalization equation is:

    $$\frac{x_{i}-\mu}{\sigma}=\frac{x_{i}-\mu_{\mathcal{B}}}{\sigma_{\mathcal{B}}} \cdot r+d, \quad \text { where } r=\frac{\sigma_{\mathcal{B}}}{\sigma}, \quad d=\frac{\mu_{\mathcal{B}}-\mu}{\sigma}$$

    In other words, we multiply the batch normalized activations by \(r\) and add \(d\), where both \(r\) and \(d\) are computed from the mini-batch statistics and moving average statistics. The trick here is to not backpropagate through \(r\) and \(d\). Though this means we ignore some of the effects of previous layers on previous mini batches, since the mini batch statistics and moving average statistics should be the same on average, the overall effect of this should cancel out on average as well.

  2. Motivation (derivation):
    The basic idea behind batch renormalization comes from the fact that we do not use the individual mini-batch statistics for batch normalization during inference. Instead, we use a moving average of the mini-batch statistics. This is because a moving average provides a better estimate of the true mean and variance compared to individual mini-batches.

    Why don’t we use the moving average during training?
    The answer has to do with the fact that during training, we need to perform backpropagation. In essence, when we use some statistics to normalize the data, we need to backpropagate through those statistics as well. If we use the statistics of activations from previous mini-batches to normalize the data, we need to account for how the previous layer affected those statistics during backpropagation. If we ignore these interactions, we could potentially cause previous layers to keep on increasing the magnitude of their activations even though it has no effect on the loss. This means that if we use a moving average, we would need to store the data from all previous mini-batches during training, which is far too expensive.

  3. Performance:
    Unfortunately, batch renormalization’s performance still degrades when the batch size decreases (though not as badly as batch normalization), meaning group normalization still has a slight advantage in the small batch size regime.

Batch-Instance Normalization

  1. Batch-Instance Normalization:
    Batch-Instance Normalization is an extension of instance normalization that attempts to account for differences in contrast and style in images. It is basically, just, an interpolation between batch normalization and instance normalization.

    Denoting the batch normalized outputs and the instance normalized outputs as \(\hat{x}^{(B)}\) and \(\hat{x}^{(I)}\) each, the batch-instance normalized output can be expressed as:

    $$\mathbf{y}=\left(\rho \cdot \hat{\mathbf{x}}^{(B)}+(1-\rho) \cdot \hat{\mathbf{x}}^{(I)}\right) \cdot \gamma+\beta$$

    The interesting aspect of batch-instance normalization is that the balancing parameter \(\rho\) is learned through gradient descent.

  2. Motivation:
    The problem with instance normalization is that it completely erases style information. Though this is beneficial in certain settings like style transfer, it can be problematic in settings like weather classification where the style (e.g. the brightness of the image) can be a crucial feature. In other words, the degree of style information that should be removed is dependent on the task at hand. Batch-instance normalization attempts to deal with this by learning how much style information should be used for each task and feature map (channel).
    Thus, B-IN extends instance normalization to account for differences in contrast and style in images.

  3. Performance:
    Batch-instance normalization outperformed batch normalization on CIFAR-10/100, ImageNet, domain adaptation, and style transfer. In image classification tasks, the value of \(\rho\) tended to be close to \(0\) or \(1\), meaning many layers used either instance or batch normalization almost exclusively. In addition, layers tended to use batch normalization more than instance normalization, which fits the intuition proposed by the authors that instance normalization serves more as a method to eliminate unnecessary style variation. On style transfer – on the other hand – the model tended to use instance normalization more, which makes sense given style is much less important in style transfer.

    The authors also found that in practice, using a higher learning rate for \(\rho\) improves performance.

    One important contribution of batch-instance normalization is that it showed that models could learn to adaptively use different normalization methods using gradient descent. This raises the question: could models learn to use an even wider variety of normalization methods?
    This nicely leads us to the next normalization method: Switchable Normalization.

Switchable Normalization

  1. Switchable Normalization:
    Switchable Normalization is a method that uses a weighted average of different mean and variance statistics from batch normalization, instance normalization, and layer normalization. Similar to batch-instance normalization, the weights were learned through backpropagation.

  2. Motivation:
    Given the different methods proposed for normalization, common questions arise, including:
    Is batch normalization still the best normalization method out-of-the-box? What if we combine different normalization methods? What if the best normalization method actually differs depending on the depth of the layer?
    Switchable Normalization aims to answer those questions.

  3. Performance:
    The authors showed that switch normalization could potentially outperform batch normalization on tasks such as image classification and object detection.

    Perhaps more interestingly, the paper showed that the statistics of instance normalization were used more heavily in earlier layers, whereas layer normalization was preferred in the later layers, and batch normalization being used in the middle. Smaller batch sizes lead to a preference towards layer normalization and instance normalization, as is expected.

Spectral Normalization

  1. Spectral Normalization:
    Spectral Normalization is a method proposed to improve the training of GANs by limiting the Lipschitz constant of the discriminator.
    The authors restrict the Lipschitz constant by normalizing the weight matrices by their largest eigenvalue (or their spectral norm – hence the name). The largest eigenvalue is computed using the power method which makes the computational cost of this method very cheap. (Compared to weight normalization, spectral normalization does not reduce the rank of the weight matrix.)1

    SN is not designed to be a replacement for batch normalization, but it gives us a very interesting look into normalization in deep learning in general.

  2. Performance:
    Experimental results show that spectral normalization improves the training of GANs with minimal additional tuning.

Further Exploration/Discussions

Though recent papers have explored different normalization methods at different depths of the network, there are still many dimensions that can be explored. In this paper, the authors show that \(L_1\) normalization performs better than batch normalization, suggesting that as we understand batch normalization better, we might be able to come up with more principled methods of normalization. This means that we might see new normalization methods use different statistics instead of changing what they compute the statistics over.

  1. Most likely a wrong statement ↩