The Learning Problem
Learning:
A computer program is said to learn from experience \(E\) with respect to some class of tasks \(T\) and performance measure \(P\), if its performance at tasks in \(T\), as measured by \(P\), improves with experience \(E\).
-
The Basic Premise/Goal of Learning:
“Using a set of observations to uncover an underlying process”Rephrased mathematically, the Goal of Learning is:
Use the Data to find a hypothesis \(g \in \mathcal{H}\), from the hypothesis set \(\mathcal{H}=\{h\}\), that approximates \(f\) well. - When to do Learning:
When:- A pattern Exists
- We cannot pin the pattern down mathematically
- We have Data
- Components of the Problem (Learning):
- Input: \(\vec{x}\)
- Output: \(y\)
- Data: \({(\vec{x}_ 1, y_ 1), (\vec{x}_ 2, y_ 2), ..., (\vec{x}_ N, y_ N)}\)
- Target Function: \(f : \mathcal{X} \rightarrow \mathcal{Y}\) (Unknown/Unobserved)
- Hypothesis: \(g : \mathcal{X} \rightarrow \mathcal{Y}\)
Learned from the Data, with the hope that it approximates \(f\) well.
- Components of the Solution:
- The Learning Model:
- The Hypothesis Set: \(\mathcal{H}=\{h\}, g \in \mathcal{H}\)
E.g. Perceptron, SVM, FNNs, etc. - The Learning Algorithm: picks \(g \approx f\) from a hypothesis set \(\mathcal{H}\)
E.g. Backprop, Quadratic Programming, etc.
- The Hypothesis Set: \(\mathcal{H}=\{h\}, g \in \mathcal{H}\)
- The Learning Model:
-
The Learning Diagram:
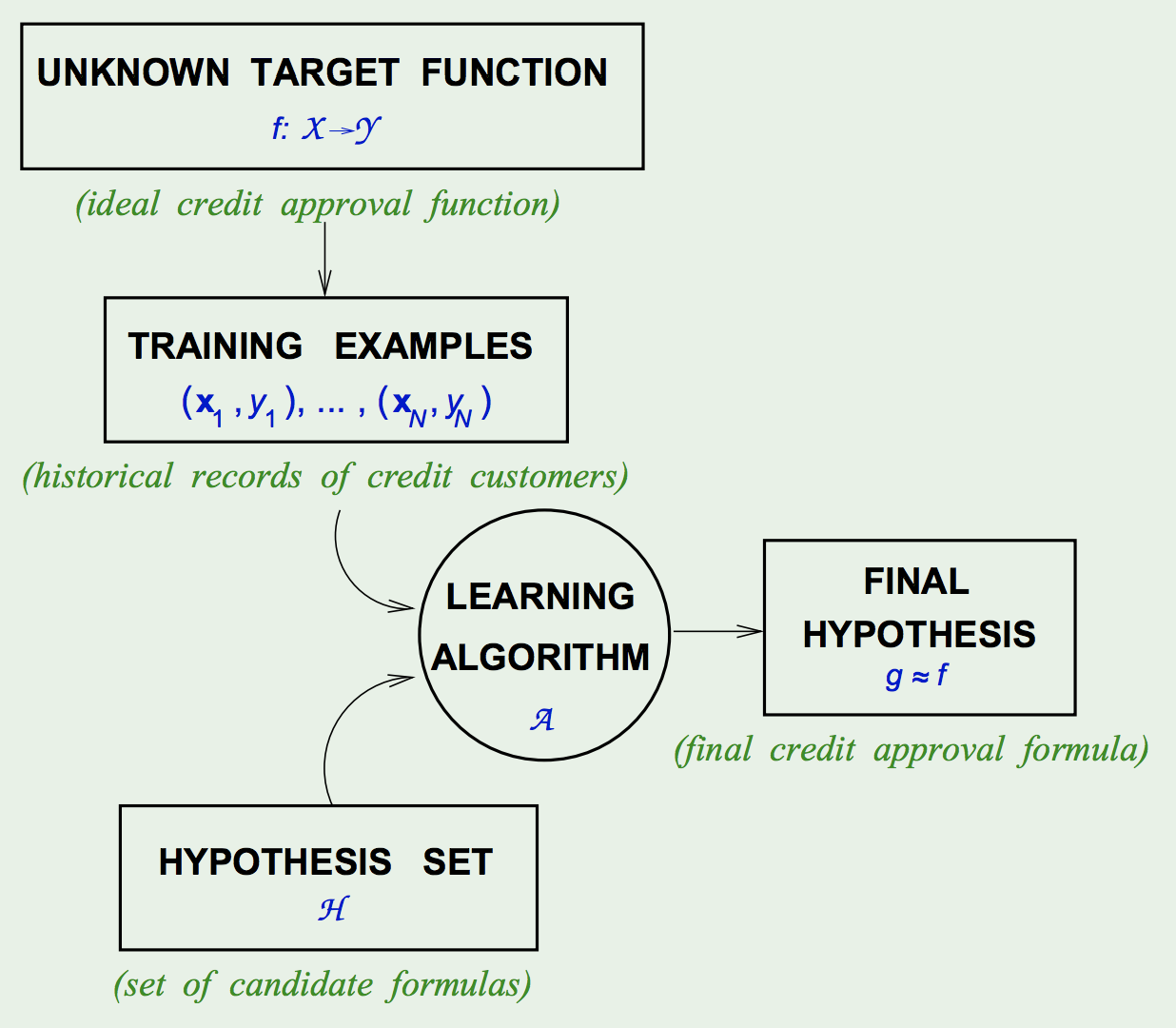
- Types of Learning:
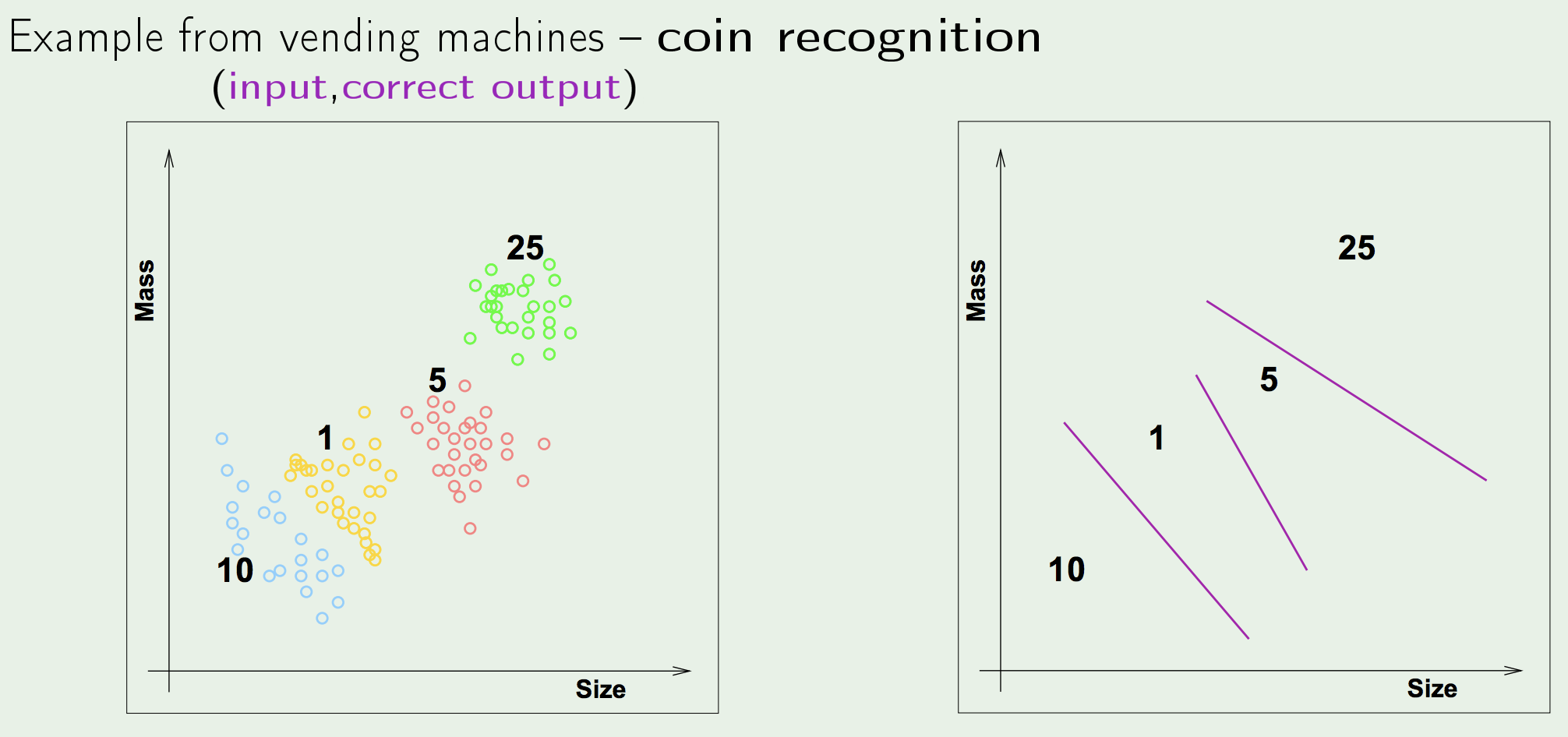
- Supervised Learning: the task of learning a function that maps an input to an output based on example input-output pairs.
- Unsupervised Learning: the task of making inferences, by learning a better representation, from some datapoints that do not have any labels associated with them.
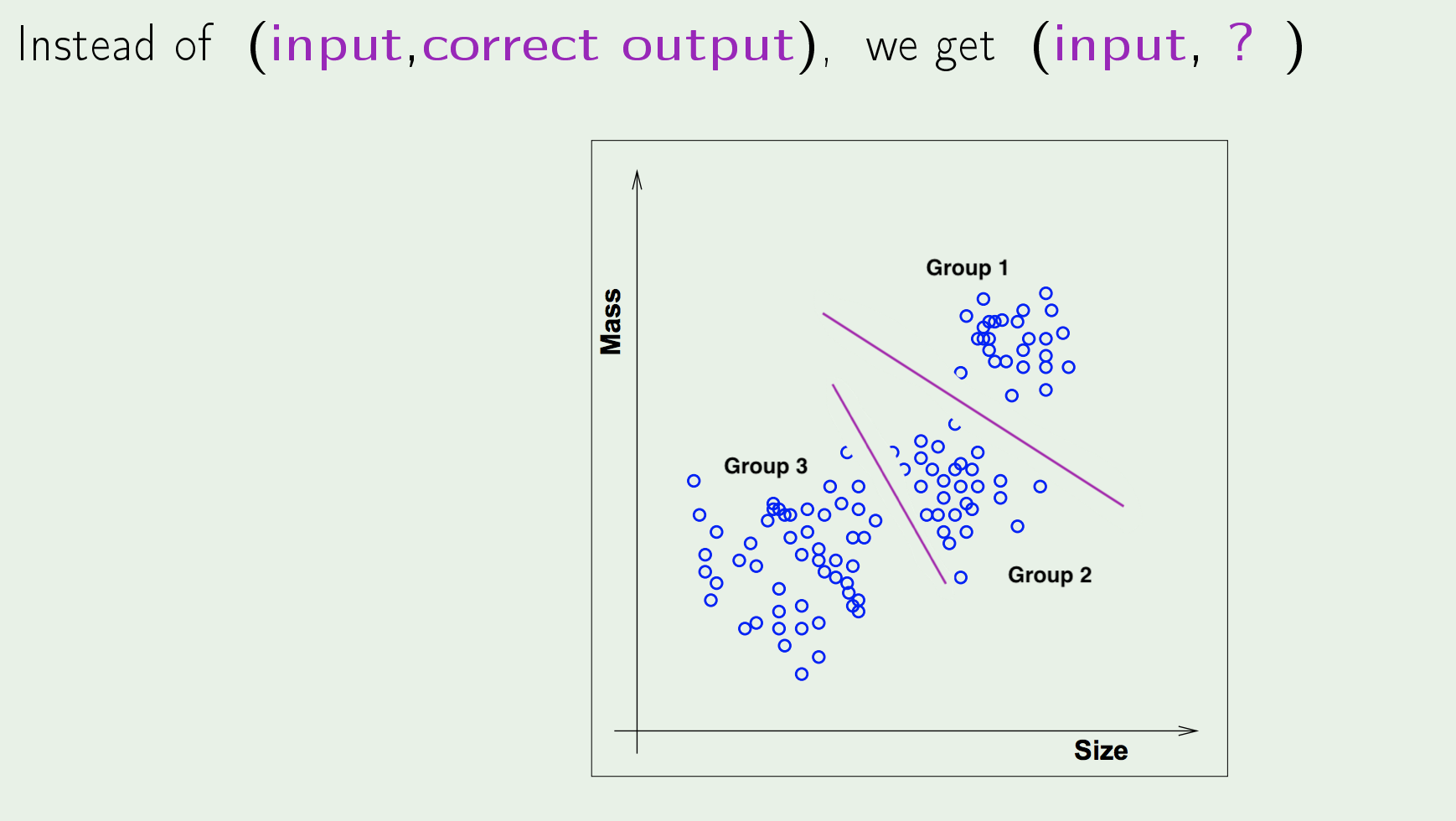
Unsupervised Learning is another name for Hebbian Learning
- Reinforcement Leaning: the task of learning how software agents ought to take actions in an environment so as to maximize some notion of cumulative reward.
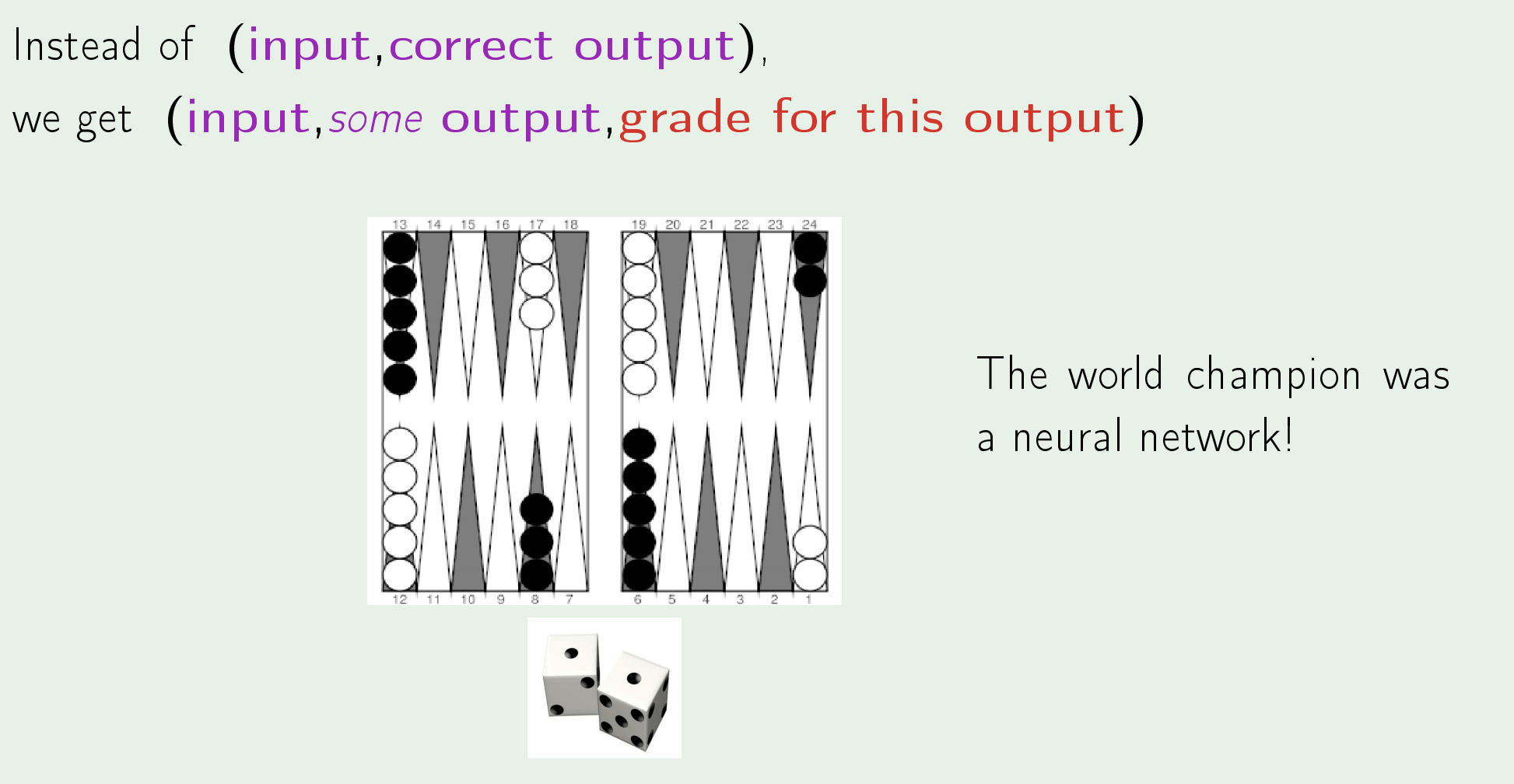
- Supervised Learning: the task of learning a function that maps an input to an output based on example input-output pairs.