• A BIT ABOUT MANIFOLDS (Blog!)

FIRST

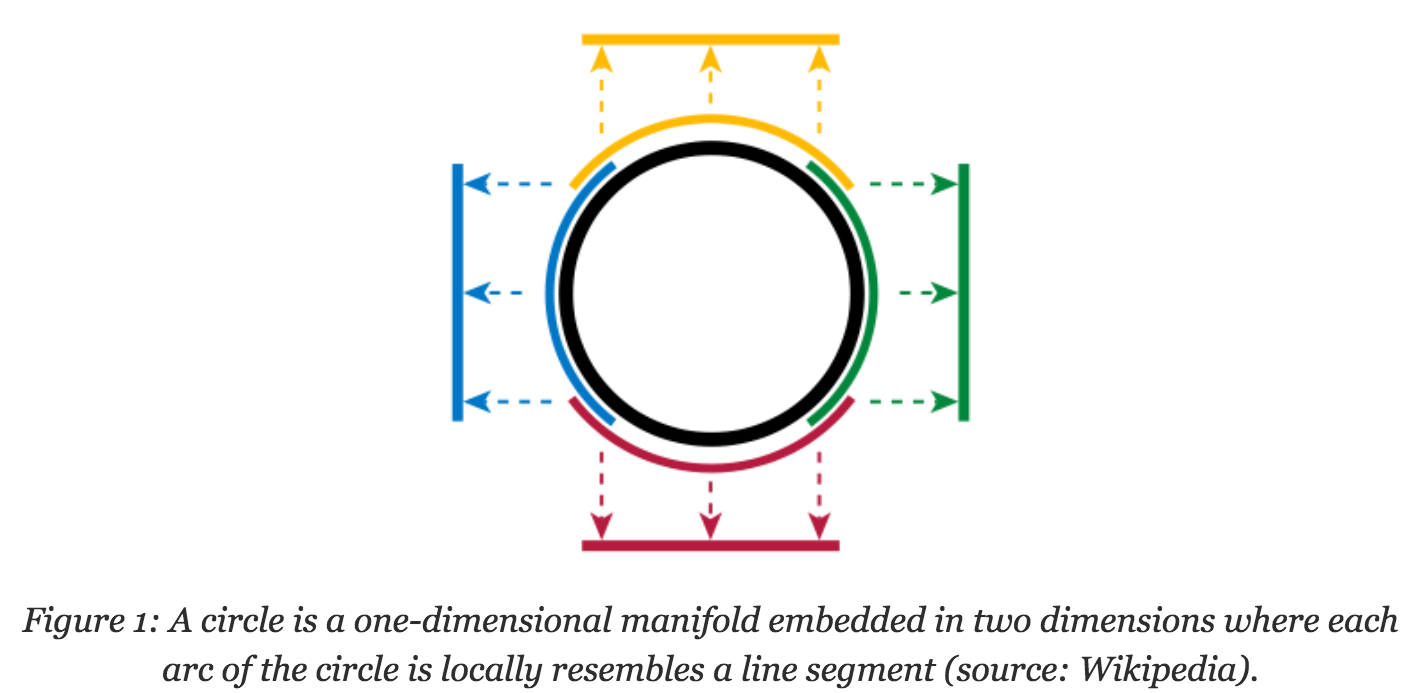
1. The Manifold Hypothesis:
   The Manifold Hypothesis states that real-world high dimensional data (such as images) lie on low-dimensional manifolds embedded in the high-dimensional space.

   Intuitively, the existence of a low-dimensional representation makes sense, because if we had to learn the entirety of the space of input-images \(256\times256\times3\) in a capacity limited NN, we will fail; but in practice we very easily can.
   Basically, learning an arbitrary \(256\times256\times3\) function would be intractable.

   • Example: Lines in \(\mathbb{R}^2\)

   • Any shape

2. Asynchronous:

3. Asynchronous:

4. Asynchronous:

5. Asynchronous:

6. Asynchronous:

7. Asynchronous:

8. Asynchronous:

• Theoretical Motivation: A lot of the natural transformations you might want to perform on an image, like translating or scaling an object in it, or changing the lighting, would form continuous curves in image space if you performed them continuously.
• Experimental Motivation: Carlsson et al. found that local patches of images form a klein bottle. On the Local Behavior of Spaces of Natural Images

SECOND

1. Asynchronous:

2. Asynchronous:

3. Asynchronous:

4. Asynchronous:

5. Asynchronous:

6. Asynchronous:

7. Asynchronous:

8. Asynchronous: