COUNT BAYESIE: PROBABLY A PROBABILITY BLOG
Review of Probability Theory (Stanford)
A First Course in Probability (Book: Sheldon Ross)
Statistics 110: Harvard
Lecture Series on Probability (following DL-book)
Probability Quora FAQs
Math review for Stat 110
Deep Learning Probability
Probability as Extended Logic
CS188 Probability Lecture (very intuitive)
Combinatorics (Notes)
Digital textbook on probability and statistics (!)
Motivation
- Uncertainty in General Systems and the need for a Probabilistic Framework:
- Inherent stochasticity in the system being modeled:
Take Quantum Mechanics, most interpretations of quantum mechanics describe the dynamics of sub-atomic particles as being probabilistic. - Incomplete observability:
Deterministic systems can appear stochastic when we cannot observe all the variables that drive the behavior of the system.i.e. Point-of-View determinism (Monty-Hall)
- Incomplete modeling:
Building a system that makes strong assumptions about the problem and discards (observed) information result in uncertainty in the predictions.
- Inherent stochasticity in the system being modeled:
-
Bayesian Probabilities and Frequentist Probabilities:
Frequentist Probabilities describe the predicted number of times that a repeatable process will result in a given output in an absolute scale.Bayesian Probabilities describe the degree of belief that a certain non-repeatable event is going to result in a given output, in an absolute scale.
We assume that Bayesian Probabilities behaves in exactly the same way as Frequentist Probabilities.
This assumption is derived from a set of “common sense” arguments that end in the logical conclusion that both approaches to probabilities must behave the same way - Truth and probability (Ramsey 1926). - Probability as an extension of Logic:
“Probability can be seen as the extension of logic to deal with uncertainty. Logic provides a set of formal rules for determining what propositions are implied to be true or false given the assumption that some other set of propositions is true or false. Probability theory provides a set of formal rules for determining the likelihood of a proposition being true given the likelihood of other propositions.” - deeplearningbook p.54
Basics
- Elements of Probability:
- Sample Space \(\Omega\): The set of all the outcomes of a stochastic experiment; where each outcome is a complete description of the state of the real world at the end of the experiment.
- Event Space \({\mathcal {F}}\): A set of events; where each event \(A \in \mathcal{F}\) is a subset of the sample space \(\Omega\) - it is a collection of possible outcomes of an experiment.
- Probability Measure \(\operatorname {P}\): A function \(\operatorname {P}: \mathcal{F} \rightarrow \mathbb{R}\) that satisfies the following properties:
- \(\operatorname {P}(A) \geq 0, \: \forall A \in \mathcal{f}\),
- \(\operatorname {P}(\Omega) = 1\), \(\operatorname {P}(\emptyset) = 0\)1
- \({\displaystyle \operatorname {P}(\bigcup_i A_i) = \sum_i \operatorname {P}(A_i) }\), where \(A_1, A_2, ...\) are disjoint events
Properties:
- \({\text { If } A \subseteq B \Longrightarrow P(A) \leq P(B)}\),
- \({P(A \cap B) \leq \min (P(A), P(B))}\),
- Union Bound: \({P(A \cup B) \leq P(A)+P(B)}\)
- \({P(\Omega \backslash A)=1-P(A)}\).
- Law of Total Probability (LOTB): \(\text { If } A_{1}, \ldots, A_{k} \text { are a set of disjoint events such that } \cup_{i=1}^{k} A_{i}=\Omega, \text { then } \sum_{i=1}^{k} P\left(A_{k}\right)=1\)
- Inclusion-Exclusion Principle:
$$\mathbb{P}\left(\bigcup_{i=1}^{n} A_{i}\right)=\sum_{i=1}^{n} \mathbb{P}\left(A_{i}\right)-\sum_{i< j} \mathbb{P}\left(A_{i} \cap A_{j}\right)+\sum_{i< j < k} \mathbb{P}\left(A_{i} \cap A_{j} \cap A_{k}\right)-\cdots+(-1)^{n-1} \sum_{i< \ldots< n} \mathbb{P}\left(\bigcap_{i=1}^{n} A_{i}\right)$$
- Properties and Proofs 110
- Random Variables:
A Random Variable is a variable that can take on different values randomly.
Formally, a random variable \(X\) is a function that maps outcomes to numerical quantities (labels), typically real numbers:$${\displaystyle X\colon \Omega \to \mathbb{R}}$$
Think of a R.V.: as a numerical “summary” of an aspect of the experiment.
Types:
- Discrete: is a variable that has a finite or countably infinite number of states
- Continuous: is a variable that is a real value
Examples:
- Bernoulli: A r.v. \(X\) is said to have a Bernoulli distribution if \(X\) has only \(2\) possible values, \(0\) and \(1\), and \(P(X=1) = p, P(X=0) = 1-p\); denoted \(\text{Bern}(p)\).
- Binomial: The distr. of #successes in \(n\) independent \(\text{Bern}(p)\) trials and its distribution is \(P(X=k) = \left(\begin{array}{l}{n} \\ {k}\end{array}\right) p^k (1-p)^{n-k}\); denoted \(\text{Bin}(n, p)\).
- Probability Distributions:
A Probability Distribution is a function that describes the likelihood that a random variable (or a set of r.v.) will take on each of its possible states.
Probability Distributions are defined in terms of the Sample Space.- Classes:
- Discrete Probability Distribution: is encoded by a discrete list of the probabilities of the outcomes, known as a Probability Mass Function (PMF).
- Continuous Probability Distribution: is described by a Probability Density Function (PDF).
- Types:
- Univariate Distributions: are those whose sample space is \(\mathbb{R}\).
They give the probabilities of a single random variable taking on various alternative values - Multivariate Distributions (also known as Joint Probability distributions): are those whose sample space is a vector space.
They give the probabilities of a random vector taking on various combinations of values.
- Univariate Distributions: are those whose sample space is \(\mathbb{R}\).
A Cumulative Distribution Function (CDF): is a general functional form to describe a probability distribution:
$${\displaystyle F(x)=\operatorname {P} [X\leq x]\qquad {\text{ for all }}x\in \mathbb {R} .}$$
Because a probability distribution P on the real line is determined by the probability of a scalar random variable X being in a half-open interval \((−\infty, x]\), the probability distribution is completely characterized by its cumulative distribution function (i.e. one can calculate the probability of any event in the event space)
- Classes:
- Probability Mass Function:
A Probability Mass Function (PMF) is a function (probability distribution) that gives the probability that a discrete random variable is exactly equal to some value.
Mathematical Definition:
Suppose that \(X: S \rightarrow A, \:\:\: (A {\displaystyle \subseteq } \mathbb{R})\) is a discrete random variable defined on a sample space \(S\). Then the probability mass function \(f_X: A \rightarrow [0, 1]\) for \(X\) is defined as:$$p_{X}(x)=P(X=x)=P(\{s\in S:X(s)=x\})$$
The total probability for all hypothetical outcomes \(x\) is always conserved:
$$\sum _{x\in A}p_{X}(x)=1$$
Joint Probability Distribution is a PMF over many variables, denoted \(P(\mathrm{x} = x, \mathrm{y} = y)\) or \(P(x, y)\).
A PMF must satisfy these properties:
- The domain of \(P\) must be the set of all possible states of \(\mathrm{x}\).
- \(\forall x \in \mathrm{x}, \: 0 \leq P(x) \leq 1\). Impossible events has probability \(0\). Guaranteed events have probability \(1\).
- \({\displaystyle \sum_{x \in \mathrm{x}} P(x) = 1}\), i.e. the PMF must be normalized.
- Probability Density Function:
A Probability Density Function (PDF) is a function (probability distribution) whose value at any given sample (or point) in the sample space can be interpreted as providing a relative likelihood that the value of the random variable would equal that sample.
The PDF is defined as the derivative of the CDF:$$f_{X}(x) = \dfrac{dF_{X}(x)}{dx}$$
A Probability Density Function \(p(x)\) does not give the probability of a specific state directly; instead the probability of landing inside an infinitesimal region with volume \(\delta x\) is given by \(p(x)\delta x\).
We can integrate the density function to find the actual probability mass of a set of points. Specifically, the probability that \(x\) lies in some set \(S\) is given by the integral of \(p(x)\) over that set.In the Univariate example, the probability that \(x\) lies in the interval \([a, b]\) is given by \(\int_{[a, b]} p(x)dx\)
A PDF must satisfy these properties:
- The domain of \(P\) must be the set of all possible states of \(x\).
- \(\forall x \in \mathrm{x}, \: 0 \leq P(x) \leq 1\). Impossible events has probability \(0\). Guaranteed events have probability \(1\).
- \(\int p(x)dx = 1\), i.e. the integral of the PDF must be normalized.
- Cumulative Distribution Function:
A Cumulative Distribution Function (CDF) is a function (probability distribution) of a real-valued random variable \(X\), or just distribution function of \(X\), evaluated at \(x\), is the probability that \(X\) will take a value less than or equal to \(x\).$$F_{X}(x)=\operatorname {P} (X\leq x)$$
The probability that \(X\) lies in the semi-closed interval \((a, b]\), where \(a < b\), is therefore
$${\displaystyle \operatorname {P} (a<X\leq b)=F_{X}(b)-F_{X}(a).}$$
Properties:
- \(0 \leq F(x) \leq 1\),
- \(\lim_{x \rightarrow -\infty} F(x) = 0\),
- \(\lim_{x \rightarrow \infty} F(x) = 1\),
- \(x \leq y \implies F(x) \leq F(y)\).
- Marginal Probability:
The Marginal Distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset.
Two-variable Case:
Given two random variables \(X\) and \(Y\) whose joint distribution is known, the marginal distribution of \(X\) is simply the probability distribution of \(X\) averaging over information about \(Y\).- Discrete:
$${\displaystyle \Pr(X=x)=\sum_ {y}\Pr(X=x,Y=y)=\sum_ {y}\Pr(X=x\mid Y=y)\Pr(Y=y)}$$
- Continuous:
$${\displaystyle p_{X}(x)=\int _{y}p_{X,Y}(x,y)\,\mathrm {d} y=\int _{y}p_{X\mid Y}(x\mid y)\,p_{Y}(y)\,\mathrm {d} y}$$
- Marginal Probability as Expectation:
$${\displaystyle p_{X}(x)=\int _{y}p_{X\mid Y}(x\mid y)\,p_{Y}(y)\,\mathrm {d} y=\mathbb {E} _{Y}[p_{X\mid Y}(x\mid y)]}$$

Marginalization: the process of forming the marginal distribution with respect to one variable by summing out the other variable
Notes:
- Marginal Distribution of a variable: is just the prior distr of the variable
- Marginal Likelihood: also known as the evidence, or model evidence, is the denominator of the Bayes equation. Its only role is to guarantee that the posterior is a valid probability by making its area sum to 1.

- both terms above are the same
- Marginal Distr VS Prior:
- Discussion
- Summary:
Basically, it’s a conceptual difference.
The prior, denoted \(p(\theta)\), denotes the probability of some event 𝜔 even before any data has been taken.
A marginal distribution is rather different. You hold a variable value and integrate over the unknown values.
But, in some contexts they are the same.
- Discrete:
- Conditional Probability:
Conditional Probability is a measure of the probability of an event given that another event has occurred.
Conditional Probability is only defined when \(P(x) > 0\) - We cannot compute the conditional probability conditioned on an event that never happens.
Definition:$$P(A|B)={\frac {P(A\cap B)}{P(B)}} = {\frac {P(A, B)}{P(B)}}$$
Intuitively, it is a way of updating your beliefs/probabilities given new evidence. It’s inherently a sequential process.
- The Chain Rule of Conditional Probability:
Any joint probability distribution over many random variables may be decomposed into conditional distributions over only one variable.
The chain rule permits the calculation of any member of the joint distribution of a set of random variables using only conditional probabilities:$$\mathrm {P} \left(\bigcap _{k=1}^{n}A_{k}\right)=\prod _{k=1}^{n}\mathrm {P} \left(A_{k}\,{\Bigg |}\,\bigcap _{j=1}^{k-1}A_{j}\right)$$
- Independence and Conditional Independence:
Two random variables \(x\) and \(y\) (or events ) are independent if their probability distribution can be expressed as a product of two factors, one involving only \(x\) and one involving only \(y\):$$\mathrm{P}(A \cap B) = \mathrm{P}(A)\mathrm{P}(B)$$
Two random variables \(A\) and \(B\) are conditionally independent given a random variable \(Y\) if the conditional probability distribution over \(A\) and \(B\) factorizes in this way for every value of \(Y\):
$$\Pr(A\cap B\mid Y)=\Pr(A\mid Y)\Pr(B\mid Y)$$
or equivalently,
$$\Pr(A\mid B\cap Y)=\Pr(A\mid Y)$$
In other words, \(A\) and \(B\) are conditionally independent given \(Y\) if and only if, given knowledge that \(Y\) occurs, knowledge of whether \(A\) occurs provides no information on the likelihood of \(B\) occurring, and knowledge of whether \(B\) occurs provides no information on the likelihood of \(A\) occurring.
Pairwise VS Mutual Independence:
- Pairwise:
$$\mathrm{P}\left(A_{m} \cap A_{k}\right)=\mathrm{P}\left(A_{m}\right) \mathrm{P}\left(A_{k}\right)$$
- Mutual Independence:
$$\mathrm{P}\left(\bigcap_{i=1}^{k} B_{i}\right)=\prod_{i=1}^{k} \mathrm{P}\left(B_{i}\right)$$
for all subsets of size \(k \leq n\)
Pairwise independence does not imply mutual independence, but the other way around is TRUE (by definition).
Notation:
- \(A\) is Independent from \(B\): \(A{\perp}B\)
- \(A\) and \(B\) are conditionally Independent given \(Y\): \(A{\perp}B \:\vert Y\)
Notes:
- Unconditional Independence is very rare (there is usually some hidden factor influencing the interaction between the two events/variables)
- Conditional Independence is the most basic and robust form of knowledge about uncertain environments
- Pairwise:
- Expectation:
The expectation, or expected value, of some function \(f(x)\) with respect to a probability distribution \(P(x)\) is the “theoretical” average, or mean value, that \(f\) takes on when \(x\) is drawn from \(P\).The Expectation of a R.V. is a weighted average of the values \(x\) that the R.V. can take – \(\operatorname {E}[X] = \sum_{x \in X} x \cdot p(x)\)
- Discrete case:
$${\displaystyle \operatorname {E}_{x \sim P} [f(X)]=f(x_{1})p(x_{1})+f(x_{2})p(x_{2})+\cdots +f(x_{k})p(x_{k})} = \sum_x P(x)f(x)$$
- Continuous case:
$${\displaystyle \operatorname {E}_ {x \sim P} [f(X)] = \int p(x)f(x)dx}$$
Linearity of Expectation:
$${\displaystyle {\begin{aligned}\operatorname {E} [X+Y]&=\operatorname {E} [X]+\operatorname {E} [Y],\\[6pt]\operatorname {E} [aX]&=a\operatorname {E} [X],\end{aligned}}}$$
Independence:
If \(X\) and \(Y\) are independent \(\implies \operatorname {E} [XY] = \operatorname {E} [X] \operatorname {E} [Y]\)
- Discrete case:
- Variance:
Variance is the expectation of the squared deviation of a random variable from its mean.
It gives a measure of how much the values of a function of a random variable \(x\) vary as we sample different values of \(x\) from its probability distribution:$$\operatorname {Var} (f(x))=\operatorname {E} \left[(f(x)-\mu )^{2}\right] = \sum_{x \in X} (x - \mu)^2 \cdot p(x)$$
Variance expanded:
$${\displaystyle {\begin{aligned}\operatorname {Var} (X)&=\operatorname {E} \left[(X-\operatorname {E} [X])^{2}\right]\\ &=\operatorname {E} \left[X^{2}-2X\operatorname {E} [X]+\operatorname {E} [X]^{2}\right]\\ &=\operatorname {E} \left[X^{2}\right]-2\operatorname {E} [X]\operatorname {E} [X]+\operatorname {E} [X]^{2}\\ &=\operatorname {E} \left[X^{2}\right]-\operatorname {E} [X]^{2}\end{aligned}}}$$
Variance as Covariance: Variance can be expressed as the covariance of a random variable with itself:
$$\operatorname {Var} (X)=\operatorname {Cov} (X,X)$$
Properties:
- \(\operatorname {Var} [a] = 0, \forall a \in \mathbb{R}\) (constant \(a\))
- \(\operatorname {Var} [af(X)] = a^2 \operatorname {Var} [f(X)]\) (constant \(a\))
- \(\operatorname {Var} [X + Y] = a^2 \operatorname {Var} [X] + \operatorname {Var} [Y] + 2 \operatorname {Cov} [X, Y]\).
Notes:
- When comparing Variances, ALWAYS NORMALIZE FIRST: Variance depends on Scale
- Standard Deviation:
The Standard Deviation is a measure that is used to quantify the amount of variation or dispersion of a set of data values.
It is defined as the square root of the variance:$${\displaystyle {\begin{aligned}\sigma &={\sqrt {\operatorname {E} [(X-\mu )^{2}]}}\\&={\sqrt {\operatorname {E} [X^{2}]+\operatorname {E} [-2\mu X]+\operatorname {E} [\mu ^{2}]}}\\&={\sqrt {\operatorname {E} [X^{2}]-2\mu \operatorname {E} [X]+\mu ^{2}}}\\&={\sqrt {\operatorname {E} [X^{2}]-2\mu ^{2}+\mu ^{2}}}\\&={\sqrt {\operatorname {E} [X^{2}]-\mu ^{2}}}\\&={\sqrt {\operatorname {E} [X^{2}]-(\operatorname {E} [X])^{2}}}\end{aligned}}}$$
Properties:
- 68% of the data-points lie within \(1 \cdot \sigma\)s from the mean
- 95% of the data-points lie within \(2 \cdot \sigma\)s from the mean
- 99% of the data-points lie within \(3 \cdot \sigma\)s from the mean
- Covariance:
Covariance is a measure of the joint variability of two random variables.
It gives some sense of how much two values are linearly related to each other, as well as the scale of these variables:$$\operatorname {cov} (X,Y)=\operatorname {E} { {\big[ }(X-\operatorname {E} [X])(Y-\operatorname {E} [Y]){ \big] } }$$
Covariance expanded:
$${\displaystyle {\begin{aligned}\operatorname {cov} (X,Y)&=\operatorname {E} \left[\left(X-\operatorname {E} \left[X\right]\right)\left(Y-\operatorname {E} \left[Y\right]\right)\right]\\&=\operatorname {E} \left[XY-X\operatorname {E} \left[Y\right]-\operatorname {E} \left[X\right]Y+\operatorname {E} \left[X\right]\operatorname {E} \left[Y\right]\right]\\&=\operatorname {E} \left[XY\right]-\operatorname {E} \left[X\right]\operatorname {E} \left[Y\right]-\operatorname {E} \left[X\right]\operatorname {E} \left[Y\right]+\operatorname {E} \left[X\right]\operatorname {E} \left[Y\right]\\&=\operatorname {E} \left[XY\right]-\operatorname {E} \left[X\right]\operatorname {E} \left[Y\right].\end{aligned}}}$$
when \({\displaystyle \operatorname {E} [XY]\approx \operatorname {E} [X]\operatorname {E} [Y]}\), this last equation is prone to catastrophic cancellation when computed with floating point arithmetic and thus should be avoided in computer programs when the data has not been centered before.
Covariance of Random Vectors:
$${\begin{aligned}\operatorname {cov} (\mathbf {X} ,\mathbf {Y} )&=\operatorname {E} \left[(\mathbf {X} -\operatorname {E} [\mathbf {X} ])(\mathbf {Y} -\operatorname {E} [\mathbf {Y} ])^{\mathrm {T} }\right]\\&=\operatorname {E} \left[\mathbf {X} \mathbf {Y} ^{\mathrm {T} }\right]-\operatorname {E} [\mathbf {X} ]\operatorname {E} [\mathbf {Y} ]^{\mathrm {T} },\end{aligned}}$$
The Covariance Matrix of a random vector \(x \in \mathbb{R}^n\) is an \(n \times n\) matrix, such that:
$$ \operatorname {cov} (X)_ {i,j} = \operatorname {cov}(x_i, x_j) \\ \operatorname {cov}(x_i, x_j) = \operatorname {Var} (x_i)$$
Interpretations:
- High absolute values of the covariance mean that the values change very much and are both far from their respective means at the same time.
- The sign of the covariance:
The sign of the covariance shows the tendency in the linear relationship between the variables:- Positive:
the variables tend to show similar behavior - Negative:
the variables tend to show opposite behavior - Reason:
If the greater values of one variable mainly correspond with the greater values of the other variable, and the same holds for the lesser values, (i.e., the variables tend to show similar behavior), the covariance is positive. In the opposite case, when the greater values of one variable mainly correspond to the lesser values of the other, (i.e., the variables tend to show opposite behavior), the covariance is negative.
- Positive:
Covariance and Variance:
$$\operatorname{Var}[X+Y]=\operatorname{Var}[X]+\operatorname{Var}[Y]+2 \operatorname{Cov}[X, Y]$$
Covariance and Independence:
If \(X\) and \(Y\) are independent \(\implies \operatorname{cov}[X, Y]=\mathrm{E}[X Y]-\mathrm{E}[X] \mathrm{E}[Y] = 0\).- Independence \(\Rightarrow\) Zero Covariance
- Zero Covariance \(\nRightarrow\) Independence
Covariance and Correlation:
If \(\operatorname{Cov}[X, Y]=0 \implies\) \(X\) and \(Y\) are Uncorrelated.- Covariance/Correlation Intuition
- Covariance and Correlation (Harvard Lecture)
- Covariance as slope of the Regression Line
- Mixtures of Distributions:
It is also common to define probability distributions by combining other simpler probability distributions. One common way of combining distributions is to construct a mixture distribution.
A Mixture Distribution is the probability distribution of a random variable that is derived from a collection of other random variables as follows: first, a random variable is selected by chance from the collection according to given probabilities of selection, and then the value of the selected random variable is realized.
On each trial, the choice of which component distribution should generate the sample is determined by sampling a component identity from a multinoulli distribution:$$P(x) = \sum_i P(x=i)P(x \vert c=i)$$
where \(P(c)\) is the multinoulli distribution over component identities.
- Bayes’ Rule:
Bayes’ Rule describes the probability of an event, based on prior knowledge of conditions that might be related to the event.$${\displaystyle P(A\mid B)={\frac {P(B\mid A)\,P(A)}{P(B)}}}$$
where,
$$P(B) =\sum_A P(B \vert A) P(A)$$
- Common Random Variables:
Discrete RVs:- Bernoulli:
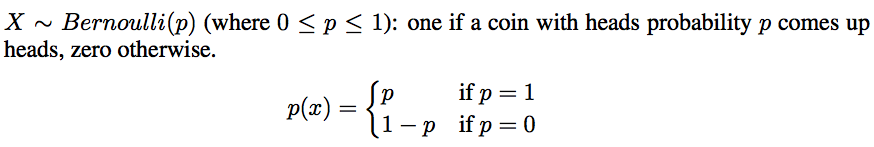
- Binomial:
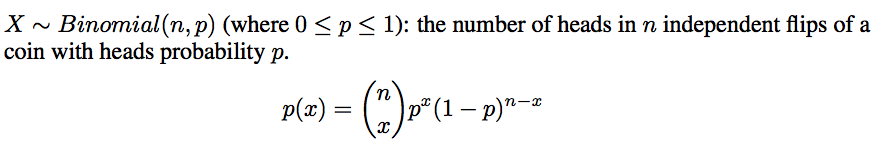
- Geometric:
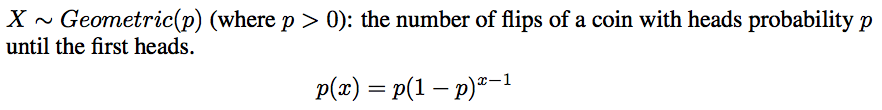
- Poisson:
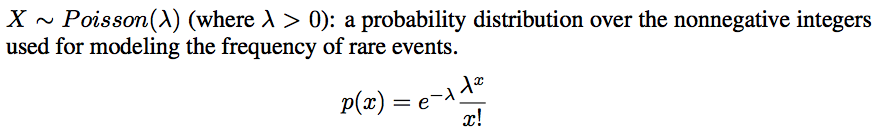
Continuous RVs:
- Uniform:
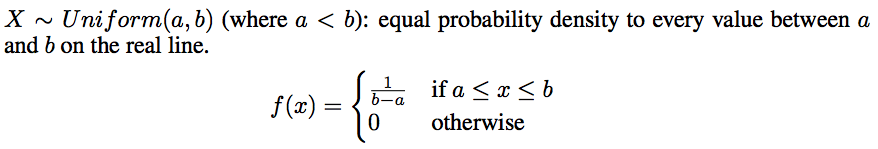
- Exponential:
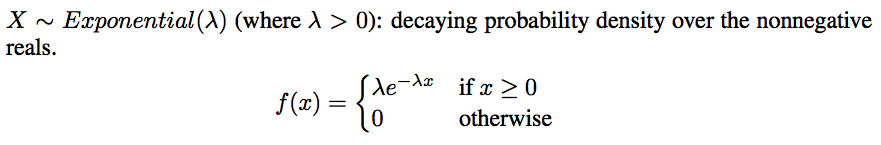
- Normal/Gaussian:
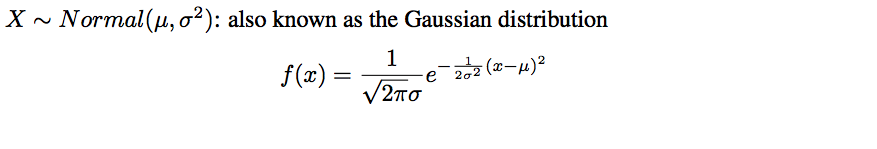
- Bernoulli:
-
Summary of Distributions:

- Formulas:
- \(\overline{X} = \hat{\mu}\),
- \(\operatorname {E}[\overline{X}]=\operatorname {E}\left[\frac{X_{1}+\cdots+X_{n}}{n}\right] = \mu\),
- \(\operatorname{Var}[\overline{X}]=\operatorname{Var}\left[\frac{X_{1}+\cdots+X_{n}}{n}\right] = \dfrac{\sigma^2}{n}\),
- \(\operatorname {E}\left[X_{i}^{2}\right]=\operatorname {Var} [X]+\operatorname {E} [X]^{2} = \sigma^{2}+\mu^{2}\),
- \(\operatorname {E}\left[\overline{X}^{2}\right]=\operatorname {E}\left[\hat{\mu}^{2}\right]=\frac{\sigma^{2}}{n}+\mu^{2}\:\), 2
-
Correlation:
In the broadest sense correlation is any statistical association, though it commonly refers to the degree to which a pair of variables are linearly related.There are several correlation coefficients, often denoted \({\displaystyle \rho }\) or \(r\), measuring the degree of correlation:
Pearson Correlation Coefficient [wiki]:
It is a measure of the linear correlation between two variables \(X\) and \(Y\).$$\rho_{X, Y}=\frac{\operatorname{cov}(X, Y)}{\sigma_{X} \sigma_{Y}}$$
where, \({\displaystyle \sigma_{X}}\) is the standard deviation of \({\displaystyle X}\) and \({\displaystyle \sigma_{Y}}\) is the standard deviation of \({\displaystyle Y}\), and \(\rho \in [-1, 1]\).
Correlation and Independence:
- Uncorrelated \(\nRightarrow\) Independent
- Independent \(\implies\) Uncorrelated
Zero correlation will indicate no linear dependency, however won’t capture non-linearity. Typical example is uniform random variable \(x\), and \(x^2\) over \([-1,1]\) with zero mean. Correlation is zero but clearly not independent.
-
Probabilistic Inference:
Probabilistic Inference: compute a desired probability from other known probabilities (e.g. conditional from joint).We generally compute Conditional Probabilities:
- \[p(\text{sun} \vert T=\text{12 pm}) = 0.99\]
- These represent the agents beliefs given the evidence
Probabilities change with new evidence:
- \(p(\text{sun} \vert T=\text{12 pm}, C=\text{Stockholm}) = 0.85\)
\(\longrightarrow\) - \[p(\text{sun} \vert T=\text{12 pm}, C=\text{Stockholm}, M=\text{Jan}) = 0.40\]
- Observing new evidence causes beliefs to be updated
Inference by Enumeration:
Problems:
- Worst-case time complexity \(\mathrm{O}\left(\mathrm{d}^{n}\right)\)
- Space complexity \(\mathrm{O}\left(\mathrm{d}^{n}\right)\) to store the joint distribution
Inference with Bayes Theorem:
- Diagnostic Probability from Causal Probability:
$$P(\text { cause } | \text { effect })=\frac{P(\text { effect } | \text { cause }) P(\text { cause })}{P(\text { effect })}$$
Discrete Distributions
-
- Bernoulli Distribution:
- A distribution over a single binary random variable.
It is controlled by a single parameter \(\phi \in [0, 1]\), which fives the probability of the r.v. being equal to \(1\).It models the probability of a single experiment with a boolean outcome (e.g. coin flip \(\rightarrow\) {heads: 1, tails: 0})
- PMF:
- \[{\displaystyle P(x)={\begin{cases}p&{\text{if }}p=1,\\q=1-p&{\text{if }}p=0.\end{cases}}}\]
- Properties:
$$P(X=1) = \phi$$
$$P(X=0) = 1 - \phi$$
$$P(X=x) = \phi^x (1 - \phi)^{1-x}$$
$$\operatorname {E}[X] = \phi$$
$$\operatorname {Var}(X) = \phi (1 - \phi)$$
- Binomial Distribution:
\({\binom {n}{k}}={\frac {n!}{k!(n-k)!}}\) is the number of possible ways of getting \(x\) successes and \(n-x\) failures
110
- Problems:
- deMortmonts/Matching problem
Sol: Inclusion-Exclusion
- Newton-Pepys: most likely event of rolling 6’s in dice
- deMortmonts/Matching problem
Notes, Tips and Tricks
-
It is more practical to use a simple but uncertain rule rather than a complex but certain one, even if the true rule is deterministic and our modeling system has the fidelity to accommodate a complex rule.
For example, the simple rule “Most birds fly” is cheap to develop and is broadly useful, while a rule of the form, “Birds fly, except for very young birds that have not yet learned to fly, sick or injured birds that have lost the ability to fly, flightless species of birds including the cassowary, ostrich and kiwi. . .” is expensive to develop, maintain and communicate and, after all this effort, is still brittle and prone to failure. - Disjoint Events (Mutually Exclusive): are events that cannot occur together at the same time
Mathematically:
- \(A_i \cap A_j = \varnothing\) whenever \(i \neq j\)
- \(p(A_i, A_j) = 0\),
-
Complexity of Describing a Probability Distribution:
A description of a probability distribution is exponential in the number of variables it models.
The number of possibilities is exponential in the number of variables. -
Probability VS Likelihood:
Probabilities are the areas under a fixed distribution
\(pr(\)data\(|\)distribution\()\)
i.e. probability of some data (left hand side) given a distribution (described by the right hand side)
Likelihoods are the y-axis values for fixed data points with distributions that can be moved..
\(L(\)distribution\(|\)observation/data\()\)Likelihood is, basically, a specific probability that can only be calculated after the fact (of observing some outcomes). It is not normalized to \(1\) (it is not a probability). It is just a way to quantify how likely a set of observation is to occur given some distribution with some parameters; then you can manipulate the parameters to make the realization of the data more “likely” (it is precisely meant for that purpose of estimating the parameters); it is a function of the parameters.
Probability, on the other hand, is absolute for all possible outcomes. It is a function of the Data. -
Maximum Likelihood Estimation:
A method that tries to find the optimal value for the mean and/or stdev for a distribution given some observed measurements/data-points. -
Variance:
When \(\text{Var}(X) = 0 \implies X = E[X] = \mu\). (not interesting) - Reason we sometimes prefer Biased Estimators: