• Principles of Risk Minimization for Learning Theory (original papers)
• Statistical Learning Theory from scratch (paper)
• The learning dynamics behind generalization and overfitting in Deep Networks
• Notes on SLT
• Mathematics of Learning (w/ proofs & necessary+sufficient conditions for learning)
• Generalization Bounds for Hypothesis Spaces
• Generalization Bound Derivation
• Overfitting isn’t simple: Overfitting Re-explained with Priors, Biases, and No Free Lunch
• 9.520/6.860: Statistical Learning Theory and Applications, Fall 2017
• What is a Hypothesis in Machine Learning? (blog)
• No Free Lunch Theorem and PAC Learning (Lec Notes!)
• Regularization and Reproducing Kernel Hilbert Spaces (ESL)
• Feasibility of learning: VC-inequality from Hoeffding (Slides)

Fundamental Theorem of Statistical Learning (binary classification):
Let \(\mathcal{H}\) be a hypothesis class of functions from a domain \(X\) to \(\{0,1\}\) and let the loss function be the \(0-1\) loss.
The following are equivalent:
\(\begin{array}{l}{\text { 1. } \mathcal{H} \text { has uniform convergence. }} \\ {\text { 2. The ERM is a PAC learning algorithm for } \mathcal{H} \text { . }} \\ {\text { 3. } \mathcal{H} \text { is } PAC \text { learnable. }} \\ {\text { 4. } \mathcal{H} \text { has finite } VC \text { dimension. }}\end{array}\)
This can be extended to regression and multiclass classification.

Proof.

Notes:

• VC dimension fully determines learnability for binary classification.
• The VC dimension doesn’t just determine learnability, it also gives a bound on the sample complexity (which can be shown to be tight).
• Lecture Slides (ref)
• Extra Notes (what you should know)

Theoretical Concepts:

• Kolmogorov Complexity:
  In Algorithmic Information Theory, the Kolmogorov Complexity of an object, such as a piece of text, is the length of the shortest computer program (in a predetermined programming language) that produces the object as output.
  It is a measure of the computational resources needed to specify the object.
  It is also known as algorithmic complexity, Solomonoff–Kolmogorov complexity, program-size complexity, descriptive complexity, or algorithmic entropy.
• Rademacher Complexity:
• Generalization Bounds:
• Sample Complexity:
• PAC-Bayes Bound:
• Kolmogorov Randomness:
• Minimum Description Length (MDL):
  The minimum description length (MDL) principle is a formalization of Occam’s razor in which the best hypothesis (a model and its parameters) for a given set of data is the one that leads to the best compression of the data.
• Minimum Message Length (MML):
  MML is a formal Information Theory restatement of Occam’s Razor: even when models are equal in goodness of fit accuracy to the observed data, the one generating the shortest overall message is more likely to be correct (where the message consists of a statement of the model, followed by a statement of data encoded concisely using that model).
• Statistical Decision Theory (ESL!)
• PAC Learnability:
  A hypothesis class \(\mathcal{H}\) is PAC learnable, if there exists a learning algorithm A, satisfying that for any \(\epsilon>0\) and \(\delta \in(0,1)\) there exist \(\mathfrak{M}(\epsilon, \delta)=\) poly \(\left(\frac{1}{\epsilon}, \frac{1}{\delta}\right)\) such that for i.i.d samples \(S^{m}=\left\{\left(x_{i}, y_{i}\right)\right\}_ {i=1}^{m}\) drawn from any distribution \(\mathcal{D}\) and \(m \geq \mathfrak{M}(\epsilon, \delta)\) the algorithm returns a hypothesis \(A\left(S^{m}\right) \in \mathcal{H}\) satisfying

  $$P_{S^{m} \sim \mathcal{D}^{m}}\left(L_{\mathcal{D}}(A(S))>\min _{h \in \mathcal{H}} L_{\mathcal{D}}(h)+\epsilon\right)<\delta$$

  To show that empirical risk minimization (ERM) is a PAC learning algorithm, we need to show that \(L_{S}(h) \approx L_{\mathcal{D}}(h)\) for all \(h\).

• Uniform Convergence:
  A hypothesis class \(\mathcal{H}\) has the uniform convergence property, if for any \(\epsilon>0\) and \(\delta \in(0,1)\) there exist \(\mathfrak{M}(\epsilon, \delta)=\) \(\text{poly}\left(\frac{1}{\epsilon}, \frac{1}{\delta}\right)\) such that for any distribution \(\mathcal{D}\) and \(m \geq \mathfrak{M}(\epsilon, \delta)\) i.i.d samples \(S^{m}=\left\{\left(x_{i}, y_{i}\right)\right\}_ {i=1}^{m} \sim \mathcal{D}^{m}\) with probability at least \(1-\delta\), \(\left\vert L_{S}^{m}(h)-L_{\mathcal{D}}(h)\right\vert <\epsilon\) for all \(h \in \mathcal{H}\).

  • For a single \(h,\) law of large numbers says \(L_{S}^{m}(h) \stackrel{m \rightarrow \infty}{\rightarrow} L_{\mathcal{D}}(h)\)
  • For loss bounded by 1 the Hoeffding inequality states:

    $$P\left(\left\vert L_{S}^{m}(h)-L_{\mathcal{D}}(h)\right\vert >\epsilon\right) \leq 2 e^{-2 \epsilon^{2} m}$$

  • The difficulty is to bound all the \(h \in \mathcal{H}\) uniformly.
• Complexity in ML:
  • Definitions of the complexity of an object (\(h\)):
    • Minimum Description Length (MDL): the number of bits for specifying an object.
    • Order of a Polynomial
  • Definitions of the complexity of a class of objects (\(\mathcal{H}\)):
    • Entropy
    • VC-dim

Statistical Learning Theory

1. Statistical Learning Theory:
   Statistical Learning Theory is a framework for machine learning drawing from the fields of statistics and functional analysis. Under certain assumptions, this framework allows us to study the question:

   How can we affect performance on the test set when we can only observe the training set?

   It is a statistical approach to Computational Learning Theory.
   
   

2. Formal Definition:
   Let:
   • \(X\): \(\:\) the vector space of all possible inputs
   • \(Y\): \(\:\) the vector space of all possible outputs
   • \(Z = X \times Y\): \(\:\) the product space of (input,output) pairs
   • \(n\): \(\:\) the number of samples in the training set
   • \(S=\left\{\left(\vec{x}_{1}, y_{1}\right), \ldots,\left(\vec{x}_{n}, y_{n}\right)\right\}=\left\{\vec{z}_{1}, \ldots, \vec{z}_{n}\right\}\): \(\:\) the training set
   • \(\mathcal{H} = f : X \rightarrow Y\): \(\:\) the hypothesis space of all functions
   • \(V(f(\vec{x}), y)\): \(\:\) an error/loss function

   Assumptions:

   • The training and test data are generated by an unknown, joint probability distribution over datasets (over the product space \(Z\), denoted: \(p_{\text{data}}(z)=p(\vec{x}, y)\)) called the data-generating process.
     • \(p_{\text{data}}\) is a joint distribution so that it allows us to model uncertainty in predictions (e.g. from noise in data) because \(y\) is not a deterministic function of \(\vec{x}\), but rather a random variable with conditional distribution \(p(y \vert \vec{x})\) for a fixed \(\vec{x}\).
   • The i.i.d. assumptions:
     • The examples in each dataset are independent from each other
     • The training set and test set are identically distributed (drawn from the same probability distribution as each other)

     A collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent.

     Informally, it says that all the variables provide the same kind of information independently of each other.

     • Discussion on the importance if i.i.d assumptions

     Summary for Motivating i.i.d Assumptions

   The Inference Problem
   Finding a function \(f : X \rightarrow Y\) such that \(f(\vec{x}) \sim y\).

   The Expected Risk:

   $$I[f]=\mathbf{E}[V(f(\vec{x}), y)]=\int_{X \times Y} V(f(\vec{x}), y) p(\vec{x}, y) d \vec{x} d y$$

   The Target Function:
   is the best possible function \(f\) that can be chosen, is given by:

   $$f=\inf_{h \in \mathcal{H}} I[h]$$

   The Empirical Risk:
   Is a proxy measure for the expected risk, based on the training set.
   It is necessary because the probability distribution \(p(\vec{x}, y)\) is unknown.

   $$I_{S}[f]=\frac{1}{n} \sum_{i=1}^{n} V\left(f\left(\vec{x}_{i}\right), y_{i}\right)$$

   
   

3. Empirical risk minimization:
   Empirical Risk Minimization (ERM) is a principle in statistical learning theory that is based on approximating the Generalization Error (True Risk) by measuring the Training Error (Empirical Risk), i.e. the performance on training data.

   A learning algorithm that chooses the function \(f_{S}\) that minimizes the empirical risk is called empirical risk minimization:

   $$R_{\mathrm{emp}}(h) = I_{S}[f]=\frac{1}{n} \sum_{i=1}^{n} V\left(f\left(\vec{x}_{i}\right), y_{i}\right)$$

   $$f_{S} = \hat{h} = \arg \min _{h \in \mathcal{H}} R_{\mathrm{emp}}(h)$$

   Complexity:
   Show

   
   

4. Definitions:
   • Generalization Error:
     AKA: Expected Risk/Error, Out-of-Sample Error¹, \(E_{\text{out}}\)
     It is a measure of how accurately an algorithm is able to predict outcome values for previously unseen data.

   • Generalization Gap:
     It is a measure of how accurately an algorithm is able to predict outcome values for previously unseen data.

     Formally:
     The generalization gap is the difference between the expected and empirical error:

     $$G =I\left[f_{n}\right]-I_{S}\left[f_{n}\right]$$

     An Algorithm is said to Generalize (achieve Generalization) if:

     $$\lim _{n \rightarrow \infty} G_n = \lim _{n \rightarrow \infty} I\left[f_{n}\right]-I_{S}\left[f_{n}\right]=0$$

     Equivalently:

     $$E_{\text { out }}(g) \approx E_{\text { in }}(g)$$

     or

     $$I\left[f_{n}\right] \approx I_{S}\left[f_{n}\right]$$

     Computing the Generalization Gap:
     Since \(I\left[f_{n}\right]\) cannot be computed for an unknown distribution, the generalization gap cannot be computed either.
     Instead the goal of statistical learning theory is to bound or characterize the generalization gap in probability:

     $$P_{G}=P\left(I\left[f_{n}\right]-I_{S}\left[f_{n}\right] \leq \epsilon\right) \geq 1-\delta_{n} \:\:\:\:\:\: (\alpha)$$

     That is, the goal is to characterize the probability \({\displaystyle 1-\delta _{n}}\) that the generalization gap is less than some error bound \({\displaystyle \epsilon }\) (known as the learning rate and generally dependent on \({\displaystyle \delta }\) and \({\displaystyle n}\)).

     Note: \(\alpha \implies \delta_n = 2e^{-2\epsilon^2n}\)

   • The Empirical Distribution:
     AKA Data-Generating Distribution
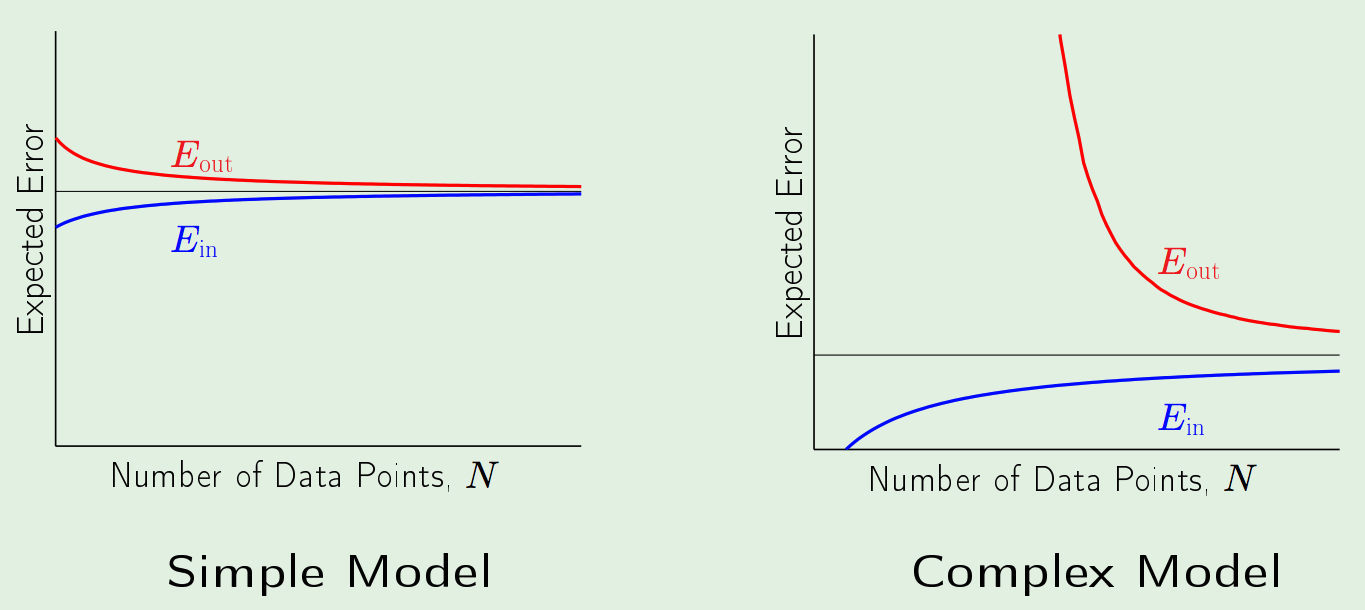
     is the discrete uniform distribution over the sample points.
   • The Approximation-Generalization Tradeoff:
     • Goal:
       Small \(E_{\text{out}}\): Good approximation of \(f\) out of sample (not in-sample).
     • The tradeoff is characterized by the complexity of the hypothesis space \(\mathcal{H}\):
       • More Complex \(\mathcal{H}\): Better chance of approximating \(f\)
       • Less Complex \(\mathcal{H}\): Better chance of generalizing out-of-sample
     • Abu-Mostafa
     • Lecture-Slides on Approximation-Generalization
   • Excess Risk (Generalization-Gap) Decomposition | Estimation-Approximation Tradeoff:
     Excess Risk is defined as the difference between the expected-risk/generalization-error of any function \(\hat{f} = g^{\mathcal{D}}\) that we learn from the data (exactly just bias-variance), and the expected-risk of the target function \(f\) (known as the bayes optimal predictor)
     • Excess Risk Decomposition Video
     • Excess Risk & Bias-Variance Lecture Slides
       
       
5. Notes:
   • Choices of Loss Functions:
     • Regression:
       • MSE: \(\: V(f(\vec{x}), y)=(y-f(\vec{x}))^{2}\)
       • MAE: \(\: V(f(\vec{x}), y)=\vert{y-f(\vec{x})}\vert\)
     • Classification:
       • Binary: \(\: V(f(\vec{x}), y)=\theta(-y f(\vec{x}))\)
         where \(\theta\) is the Heaviside Step Function.
   • Training Data, Errors, and Risk:
     • Training-Error is the Empirical Risk
       • It is a proxy for the Generalization Error/Expected Risk
       • This is what we minimize
     • Test-Error is an approximation to the Generalization Error/Expected Risk
       • This is what we (can) compute to ensure that minimizing Training-Err/Empirical-Risk (ERM) also minimized the Generalization-Err/Expected-Risk (which we can’t compute directly)
   • Why the goal is NOT to minimize \(E_{\text{in}}\) completely (intuition):
     Basically, if you have noise in the data; then fitting the (finite) training-data completely; i.e. minimizing the in-sample-err completely will underestimate the out-of-sample-err.
     Since, if noise existed AND you fit training-data completely \(E_{\text{in}} = 0\) THEN you inherently have fitted the noise AND your performance on out-sample will be lower.

The Vapnik-Chervonenkis (VC) Theory

The Bias-Variance Decomposition Theory

• Bias and Variance Latest Research: A Modern Take on the Bias-Variance Tradeoff in Neural Networks
• Ditto: On the Bias-Variance Tradeoff: Textbooks Need an Update

1. The Bias-Variance Decomposition Theory:
   The Bias-Variance Decomposition Theory is a way to quantify the Approximation-Generalization Tradeoff.

   Assumptions:

   • The analysis is done over the entire data-distribution
   • The target function \(f\) is already known; and you’re trying to answer the question:
     “How can \(\mathcal{H}\) approximate \(f\) over all? not just on your sample.”
   • Applies to real-valued targets (can be extended)
   • Use Square Error (can be extended)
     
     
2. The Bias-Variance Decomposition:
   The Bias-Variance Decomposition is a way of analyzing a learning algorithm’s expected out-of-sample error² as a sum of three terms:
   • Bias: is an error from erroneous assumptions in the learning algorithm.
   • Variance: is an error from sensitivity to small fluctuations in the training set.
   • Irreducible Error (resulting from noise in the problem itself)

   Equivalently, Bias and Variance measure two different sources of errors in an estimator:

   • Bias: measures the expected deviation from the true value of the function or parameter.

     AKA: Approximation Error³ (statistics) How well can \(\mathcal{H}\) approximate the target function ‘\(f\)’

   • Variance: measures the deviation from the expected estimator value that any particular sampling of the data is likely to cause.

     AKA: Estimation (Generalization) Error (statistics) How well we can zoom in on a good \(h \in \mathcal{H}\)

   Bias-Variance Decomposition Formula:
   For any function \(\hat{f} = g^{\mathcal{D}}\) we select, we can decompose its expected (out-of-sample) error on an unseen sample \(x\) as:

   $$\mathbb{E}_{\mathbf{x}}\left[(y-\hat{f}(x))^{2}\right]=(\operatorname{Bias}[\hat{f}(x)])^{2}+\operatorname{Var}[\hat{f}(x)]+\sigma^{2}$$

   Where:

   • Bias:

     $$\operatorname{Bias}[\hat{f}(x)]=\mathbb{E}_{\mathbf{x}}[\hat{f}(x)]-f(x)$$

   • Variance:

     $$\operatorname{Var}[\hat{f}(x)]=\mathbb{E}_{\mathbf{x}}\left[\hat{f}(x)^{2}\right]-\mathbb{E}_{\mathbf{x}}[\hat{f}(x)]^{2}$$

     and the expectation ranges over different realizations of the training set \(\mathcal{D}\).

3. The Bias-Variance Tradeoff:
   is the property of a set of predictive models whereby, models with a lower bias (in parameter estimation) have a higher variance (of the parameter estimates across samples) and vice-versa.

   Effects of Bias:

   • High Bias: simple models, lead to underfitting.
   • Low Bias: complex models, lead to overfitting.

   Effects of Variance:

   • High Variance: complex models, lead to overfitting.

   • Low Variance: simple models, lead to underfitting.

   • The Tradeoff:
   • Bias-Variance Example End2End
     
     
4. Derivation:

   $${\displaystyle {\begin{aligned}\mathbb{E}_{\mathcal{D}} {\big [}I[g^{(\mathcal{D})}]{\big ]}&=\mathbb{E}_{\mathcal{D}} {\big [}\mathbb{E}_{x}{\big [}(g^{(\mathcal{D})}-y)^{2}{\big ]}{\big ]}\\ &=\mathbb{E}_{x} {\big [}\mathbb{E}_{\mathcal{D}}{\big [}(g^{(\mathcal{D})}-y)^{2}{\big ]}{\big ]}\\ &=\mathbb{E}_{x}{\big [}\mathbb{E}_{\mathcal{D}}{\big [}(g^{(\mathcal{D})}- f -\varepsilon)^{2}{\big ]}{\big ]} \\&=\mathbb{E}_{x}{\big [}\mathbb{E}_{\mathcal{D}} {\big [}(f+\varepsilon -g^{(\mathcal{D})}+\bar{g}-\bar{g})^{2}{\big ]}{\big ]}\\ &=\mathbb{E}_{x}{\big [}\mathbb{E}_{\mathcal{D}} {\big [}(\bar{g}-f)^{2}{\big ]}+\mathbb{E}_{\mathcal{D}} [\varepsilon ^{2}]+\mathbb{E}_{\mathcal{D}} {\big [}(g^{(\mathcal{D})} - \bar{g})^{2}{\big ]}+2\: \mathbb{E}_{\mathcal{D}} {\big [}(\bar{g}-f)\varepsilon {\big ]}+2\: \mathbb{E}_{\mathcal{D}} {\big [}\varepsilon (g^{(\mathcal{D})}-\bar{g}){\big ]}+2\: \mathbb{E}_{\mathcal{D}} {\big [}(g^{(\mathcal{D})} - \bar{g})(\bar{g}-f){\big ]}{\big ]}\\ &=\mathbb{E}_{x}{\big [}(\bar{g}-f)^{2}+\mathbb{E}_{\mathcal{D}} [\varepsilon ^{2}]+\mathbb{E}_{\mathcal{D}} {\big [}(g^{(\mathcal{D})} - \bar{g})^{2}{\big ]}+2(\bar{g}-f)\mathbb{E}_{\mathcal{D}} [\varepsilon ]\: +2\: \mathbb{E}_{\mathcal{D}} [\varepsilon ]\: \mathbb{E}_{\mathcal{D}} {\big [}g^{(\mathcal{D})}-\bar{g}{\big ]}+2\: \mathbb{E}_{\mathcal{D}} {\big [}g^{(\mathcal{D})}-\bar{g}{\big ]}(\bar{g}-f){\big ]}\\ &=\mathbb{E}_{x}{\big [}(\bar{g}-f)^{2}+\mathbb{E}_{\mathcal{D}} [\varepsilon ^{2}]+\mathbb{E}_{\mathcal{D}} {\big [}(g^{(\mathcal{D})} - \bar{g})^{2}{\big ]}{\big ]}\\ &=\mathbb{E}_{x}{\big [}(\bar{g}-f)^{2}+\operatorname {Var} [y]+\operatorname {Var} {\big [}g^{(\mathcal{D})}{\big ]}{\big ]}\\ &=\mathbb{E}_{x}{\big [}\operatorname {Bias} [g^{(\mathcal{D})}]^{2}+\operatorname {Var} [y]+\operatorname {Var} {\big [}g^{(\mathcal{D})}{\big ]}{\big ]}\\ &=\mathbb{E}_{x}{\big [}\operatorname {Bias} [g^{(\mathcal{D})}]^{2}+\sigma ^{2}+\operatorname {Var} {\big [}g^{(\mathcal{D})}{\big ]}{\big ]}\\ \end{aligned}}}$$

   where:
   \(\overline{g}(\mathbf{x})=\mathbb{E}_{\mathcal{D}}\left[g^{(\mathcal{D})}(\mathbf{x})\right]\) is the average hypothesis over all realization of \(N\) data-points \(\mathcal{D}_ i\), and \({\displaystyle \varepsilon }\) and \({\displaystyle {\hat {f}}} = g^{(\mathcal{D})}\) are independent.

   Derivation with Wikipedia Notation

5. Results and Takeaways of the Decomposition:
   Match the “Model Complexity” to the Data Resources, NOT to the Target Complexity.
   
   
   
   

   Analogy to the Approximation-Generalization Tradeoff

   • Learning and Approximating are NOT the same thing (refer to the end2end example above)
     • When Approximating, you can match the complexity of your model to the complexity of the “known” target function: a linear model is better at approximating a sine wave
     • When Learning, you should only use a model as complex as the amount of data you have to settle on a good approximation of the “Unknown” target function: a constant model is better at learning an approximation of a sine wave from 2 sample data points
6. Measuring the Bias and Variance:
   • Training Error: reflects Bias, NOT variance
   • Test Error: reflects Both
7. Reducing the Bias and Variance, and Irreducible Err:
   • Adding Good Feature:
     • Decrease Bias
   • Adding Bad Feature:
     • Doesn’t affect (increase) Bias much
   • Adding ANY Feature:
     • Increases Variance
   • Adding more Data:
     • Decreases Variance
     • (May) Decreases Bias: if \(h\) can fit \(f\) exactly.
   • Noise in Test Set:
     • Affects ONLY Irreducible Err
   • Noise in Training Set:
     • Affects BOTH and ONLY Bias and Variance
   • Dimensionality Reduction:
     • Decrease Variance (by simplifying models)
   • Feature Selection:
     • Decrease Variance (by simplifying models)
   • Regularization:
     • Increase Bias
     • Decrease Variance
   • Increasing # of Hidden Units in ANNs:
     • Decrease Bias
     • Increase Variance
   • Increasing # of Hidden Layers in ANNs:
     • Decrease Bias
     • Increase Variance
   • Increasing \(k\) in K-NN:
     • Increase Bias
     • Decrease Variance
   • Increasing Depth in Decision-Trees:
     • Increase Variance
   • Boosting:
     • Decreases Bias
   • Bagging:
     • Reduces Variance
   • We Cannot Reduce the Irreducible Err
     
     
8. Bias-Variance Decomposition Analysis vs. VC-Analysis:
   
   • Caltech Comparison on Learning Curves
   • Example on Linear Regression (Caltech)
9. Application of the Decomposition to Classification:
   A similar decomposition exists for:
   • Classification w/ \(0-1\) loss
   • Probabilistic Classification w/ Squared Error
10. Bias-Variance Decomposition and Risk (Excess Risk Decomposition):
    The Bias-Variance Decomposition analyzes the behavior of the Expected Risk/Generalization Error for any function \(\hat{f}\):

    $$R(\hat{f}) = \mathbb{E}\left[(y-\hat{f}(x))^{2}\right]=(\operatorname{Bias}[\hat{f}(x)])^{2}+\operatorname{Var}[\hat{f}(x)]+\sigma^{2}$$

    Assuming that \(y = f(x) + \epsilon\).

    The Bayes Optimal Predictor is \(f(x) = \mathbb{E}[Y\vert X=x]\).

    The Excess Risk is:

    $$\text{ExcessRisk}(\hat{f}) = R(\hat{f}) - R(f)$$

    Excess Risk Decomposition:
    We add and subtract the target function \(f_{\text{target}}=\inf_{h \in \mathcal{H}} I[h]\) that minimizes the (true) expected risk:

    $$\text{ExcessRisk}(\hat{f}) = \underbrace{\left(R(\hat{f}) - R(f_{\text{target}})\right)}_ {\text { estimation error }} + \underbrace{\left(R(f_{\text{target}}) - R(f)\right)}_ {\text { approximation error }}$$

    The Bias-Variance Decomposition for Excess Risk:

    • Re-Writing Excess Risk:

      $$\text{ExcessRisk}(\hat{f}) = R(\hat{f}) - R(f) = \mathbb{E}\left[(y-\hat{f}(x))^{2}\right] - \mathbb{E}\left[(y-f(x))^{2}\right]$$

      which is equal to:

      $$R(\hat{f}) - R(f) = \mathbb{E}\left[(f(x)-\hat{f}(x))^{2}\right]$$

    $$\mathbb{E}\left[(f(x)-\hat{f}(x))^{2}\right] = (\operatorname{Bias}[\hat{f}(x)])^{2}+\operatorname{Var}[\hat{f}(x)]$$

    • if you dont want to mess with stat-jargon; lemme rephrase:
      is the minimizer \({\displaystyle f=\inf_{h \in \mathcal{H}} I[h]}\) where \(I[h]\) is the expected-risk/generalization-error (assume MSE);
      is it \(\overline{f}(\mathbf{x})=\mathbb{E}_ {\mathcal{D}}\left[f^{(\mathcal{D})}(\mathbf{x})\right]\) the average hypothesis over all realizations of \(N\) data-points \(\mathcal{D}_ i\)??

Generalization Theory

• Generalization Bounds: PAC-Bayes, Rademacher, ERM, etc. (Notes!)
• Deep Learning Generalization (blog!)

1. Generalization Theory:

   Approaches to (Notions of) Quantitative Description of Generalization Theory:

   • VC Dimension
   • Rademacher Complexity
   • PAC-Bayes Bound

   Prescriptive vs Descriptive Theory:

   • Prescriptive: only attaches a label to the problem, without giving any insight into how to solve the problem.
   • Descriptive: describes the problem in detail (e.g. by providing cause) and allows you to solve the problem.

   Generalization Theory Notions consist of attaching a descriptive label to the basic phenomenon of lack of generalization. They are hard to compute for today’s complicated ML models, let alone to use as a guide in designing learning systems.
   Generalization Bounds as Descriptive Labels:

   • Rademacher Complexity:
     Assumptions

     
     

2. Overfitting:
   One way to summarize Overfitting is:
   discovering patterns in data that do not exist in the intended application.
   The typical case of overfitting “decreasing loss only on the training set and increasing the loss on the validation set” is only one example of this.

   The question then is how we prevent overfitting from occurring.
   The problem is that we cannot know apriori what patterns will generalize from the dataset.

   No-Free-Lunch (NFL) Theorem:

   • NFL Theorems for Supervised Machine Learning:
     • In his 1996 paper The Lack of A Priori Distinctions Between Learning Algorithms, David Wolpert examines if it is possible to get useful theoretical results with a training data set and a learning algorithm without making any assumptions about the target variable.
     • Wolpert proves that given a noise-free data set (i.e. no random variation, only trend) and a machine learning algorithm where the cost function is the error rate, all machine learning algorithms are equivalent when assessed with a generalization error rate (the model’s error rate on a validation data set).
     • Extending this logic he demonstrates that for any two algorithms, A and B, there are as many scenarios where A will perform worse than B as there are where A will outperform B. This even holds true when one of the given algorithms is random guessing.
     • This is because nearly all (non-rote) machine learning algorithms make some assumptions (known as inductive or learning bias) about the relationships between the predictor and target variables, introducing bias into the model.
       The assumptions made by machine learning algorithms mean that some algorithms will fit certain data sets better than others. It also (by definition) means that there will be as many data sets that a given algorithm will not be able to model effectively.
       How effective a model will be is directly dependent on how well the assumptions made by the model fit the true nature of the data.
     • Implication: you can’t get good machine learning “for free”.
       You must use knowledge about your data and the context of the world we live in (or the world your data lives in) to select an appropriate machine learning model.
       There is no such thing as a single, universally-best machine learning algorithm, and there are no context or usage-independent (a priori) reasons to favor one algorithm over all others.
   • NFL Theorem for Search/Optimization:
     • All algorithms that search for an extremum of a cost function perform exactly the same when averaged over all possible cost functions. So, for any search/optimization algorithm, any elevated performance over one class of problems is exactly paid for in performance over another class.
     • It state that any two optimization algorithms are equivalent when their performance is averaged across all possible problems.
     • Wolpert and McReady essentially say that you need some prior knowledge that is encoded in your algorithm in order to search well.
       They created the theorem to give an easy counter example to researchers that would create a (tweak on an) algorithm and claimed that it would work better on all possible problems. It can’t. There’s a proof. If you have a good algorithm, it must in some way fit on your problem space, and you will have to investigate how.
   • Explanation through a thought experiment:
   • Main Concept: Generalizing is extrapolating to new data. To do that you need to make assumptions and for problems where the assumptions don’t hold you will be suboptimal.
   • Practical Implications:
     • Bias-free learning is futile because a learner that makes no a priori assumptions will have no rational basis for creating estimates when provided new, unseen input data.
       Models are simplifications of a specific component of reality (observed with data). To simplify reality, a machine learning algorithm or statistical model needs to make assumptions and introduce bias (known specifically as inductive or learning bias).
       The assumptions of an algorithm will work for some data sets but fail for others.
     • This shows that we need some restriction on \(\mathcal{H}\) even for the realizable PAC setting. We cannot learn arbitrary set of hypothesis, there is no free lunch.
     • There is no universal (one that works for all \(\mathcal{H}\)) learning algorithm.
       I.e., if the algorithm \(A\) has no idea about \(\mathcal{H},\) even the singleton hypothesis class \(\mathcal{H}=\{h\}\) (as in the statement of the theorem) is not PAC learnable.
     • Why do we have to fix a hypothesis class when coming up with a learning algorithm? Can we “just learn”?
       The NFL theorem formally shows that the answer is NO.
     • Counter the following claim: “My machine learning algorithm/optimization strategy is the best, always and forever, for all the scenarios”.
     • Always check your assumptions before relying on a model or search algorithm.
     • There is no “super algorithm” that will work perfectly for all datasets.
     • Variable length and redundant encodings are not covered by the NFL theorems. Does Genetic Programming get a pass?
     • NFL theorems are like a statistician sitting with his head in the fridge, and his feet in the oven. On average, his temperature is okay! NFL theorems prove that the arithmetic mean of performance is constant over all problems, it doesn’t prove that for other statistics this is the case. There has been an interesting ‘counter’ proof, where a researcher proved that for a particular problem space, a hill-climber would outperform a hill-descender on 90% of the problem instances, and did that by virtue of being exponentially worse on the remaining 10% of the problems. Its average performance abided by the NFL theorem and the two algorithms were equal when looking at mean performance, yet the hill-climber was better in 90% of the problems, i.e., it had a much better median performance. So is there maybe a free appetizer?
     • While no one model/algorithm works best for every problem, it may be that one model/algorithm works best for all real-world problems, or all problems that we care about, practically speaking.
   • No Free Lunch Theorems Main Site
   • No Free Lunch Theorem (Lec Notes)
   • Machine Learning Theory - NFL Theorem (Lec Notes)
   • Overfitting isn’t simple: Overfitting Re-explained with Priors, Biases, and No Free Lunch (Blog)
   • Learning as Refining the Hypothesis Space (Blog-Paper)
   • All Models Are Wrong (Blog)
   • Does the ‘no free lunch’ theorem also apply to deep learning? (Quora)