Essence of LA - 3b1b
LA (Stanford Review)

Definitions and Intuitions

1. Linear Algebra:
   Linear Algebra is about two operations on a list of numbers:
   1. Scalar Multiplication
   2. Vector Addition
2. Vectors:
   Think of each element in the vector as a scalar that scales the corresponding basis vectors.

   Meaning, think about how each one stretches or squishes vectors (in this case, the basis vectors \(\hat{i}, \hat{j}\))

   $$\begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \color{red} x \color{red} {\underbrace{\begin{bmatrix} 1 \\ 0 \end{bmatrix}}_ {\hat{i}}} + \color{red} y \color{red} {\underbrace{\begin{bmatrix} 0 \\ 1 \end{bmatrix}}_ {\hat{j}}} = \begin{bmatrix} 1\times x + 0 \times y \\ 0\times x + 1 \times y \end{bmatrix} $$

   How to think of vectors? Three Perspectives: Three Perspectives on Vectors:

   • Physics: an arrow pointing in space defined by the length and direction of the arrow.
   • CS: vectors are Ordered Lists of numbers.
   • Math: a vector is any object that can be (1) added to another vector (2) multiplied by a scalar value.

   The coordinates of a Vector:
   Think about the coordinates as a list of numbers that tells you how to get from the tail of the arrow to its tip.
   Each coordinate at the \(i\)th index tells you how many “steps” to take in that dimension (\(i\)th dimension).
   E.g. for the \(2-\)D case, the first coordinate dictates the steps in the \(x\) dimension, and the second coordinate the steps in the \(y\) dimension.
   Example 2D

   You can completely specify a vector with its list of coordinates (uniquely).

   Vector Addition:
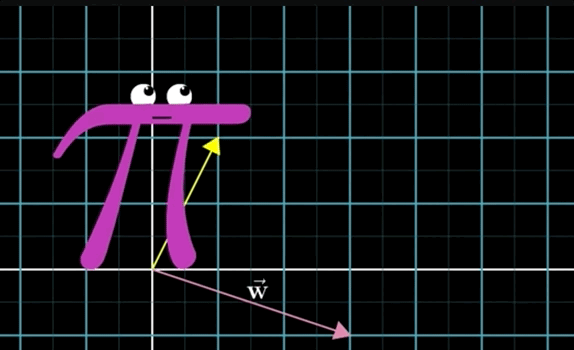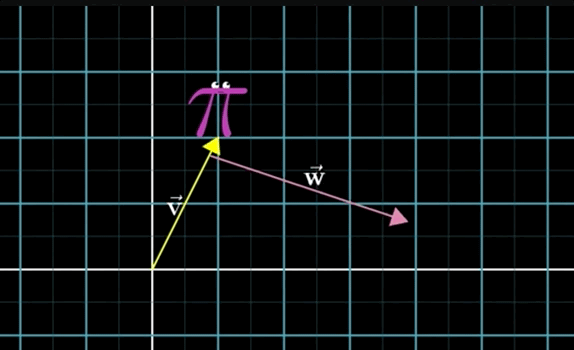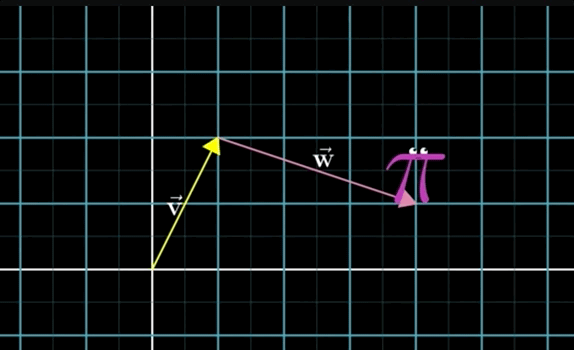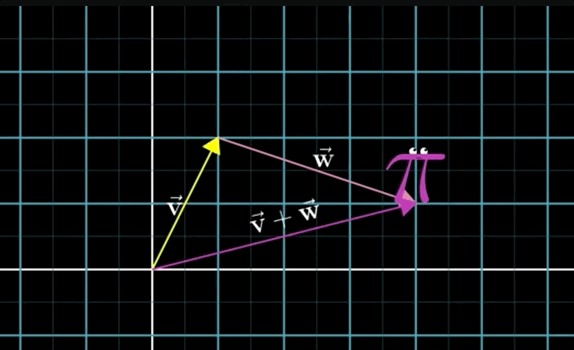
   To add the two vectors \(\overrightarrow{\mathbf{v}} + \overrightarrow{\mathbf{w}}\):

   • Move the tail of the second vector \(\overrightarrow{\mathbf{w}}\) to the tip of the first vector \(\overrightarrow{\mathbf{v}}\)
   • Draw an arrow from the tail of \(\overrightarrow{\mathbf{v}}\) to the new tip of \(\overrightarrow{\mathbf{w}}\).
   • This new arrow (vector) is the sum example

   • Intuition:
     Essentially, you are taking a step in the first vector direction then another step in the second vector direction. You can do so by moving the tail of the second vector to the tip of the first vector, essentially taking a step in that direction, then take a step in the direction (and length) of the second vector:
     Visualization

   • Vector Addition Numerically:
     

   Scalar Multiplication:
   

3. Span:
   The Span of two vectors \(\mathbf{v}, \mathbf{w}\) is the set of all linear combinations of the two vectors:

   $$a \mathbf{v} + b \mathbf{w} \: ; \: a,b \in \mathbb{R}$$

   I.E. What are all the possible vectors you can create using the two fundamental operations on two vectors: vector addition and scalar multiplication.

   As long as each vector does not point in the same direction as another vector, you can reach all possible dimensions as the number of vectors.
   I.E. if you cannot create the vector using the other vectors you have, then it is pointing in a new direction.

4. Linearly Dependent Vectors:
   If one vector is in the span of the other vectors.
   Mathematically:

   $$a \vec{v}+b \vec{w}+c \vec{u}=\overrightarrow{0} \implies a=b=c=0$$

5. The Basis:
   The Basis of a vector space is a set of linearly independent vectors that span the full space.

6. Matrix as a Linear Transformation:
   Note: A Transformation == Function \(\iff\) Linear Transformation == Linear Function.
   With vectors as inputs and vectors as outputs.

   Summary:

   1. Each column is a transformed version of the basis vectors (e.g. \(\hat{i}, \hat{j}\))
   2. The result of a Matrix-Vector Product is the linear combination of the vectors with the appropriate transformed coordinate/basis vectors

      i.e. Matrix-Vector Product is a way to compute what the corresponding linear transformation does to the given vector.

   Matrix as a Linear Transformation:
   Always think of Matrices as Transformations of Space:

   • A Matrix represents a specific linear transformation
     • Where the columns represent the coordinates of the transformed basis vectors
   • & Multiplying a matrix by a vector is EQUIVALENT to Applying the transformation to that vector

     The word “transformation” suggests that you think using movement
     If a transformation takes some input vector to some output vector, we imagine that input vector moving over to the output vector.
     Then to understand the transformation as a whole, we might imagine watching every possible input vector move over to its corresponding output vector.
     This transformation/“movement” is Linear, if it keeps all the vectors parallel and evenly spaced, and fixes the origin.

   Matrices and Vectors | The Matrix-Vector Product:
   Again, We think of each element in a vector as a scalar that scales the corresponding basis vectors.

   • Thus, if we know how the basis vectors get transformed, we can then just scale them (by multiplying with our vector elements).
     Mathematically, we think of the vector:

     $$\mathbf{v} = \begin{bmatrix}x \\y \end{bmatrix} = x\hat{i} + y\hat{j}$$

     and its transformed version:

     $$\text{Transformed } \mathbf{v} = x (\text{Transformed } \hat{i}) + y (\text{Transformed } \hat{j})$$

     \(\implies\) we can describe where any vector \(\mathbf{v}\) go, by describing where the basis vectors will land.

     If you’re given a two-by-two matrix describing a linear transformation and some specific vector and you want to know where that linear transformation takes that vector, you can (1) take the coordinates of the vector (2) multiply them by the corresponding columns of the matrix, (3) then add together what you get.
     This corresponds with the idea of adding the scaled versions of our new basis vectors.
     

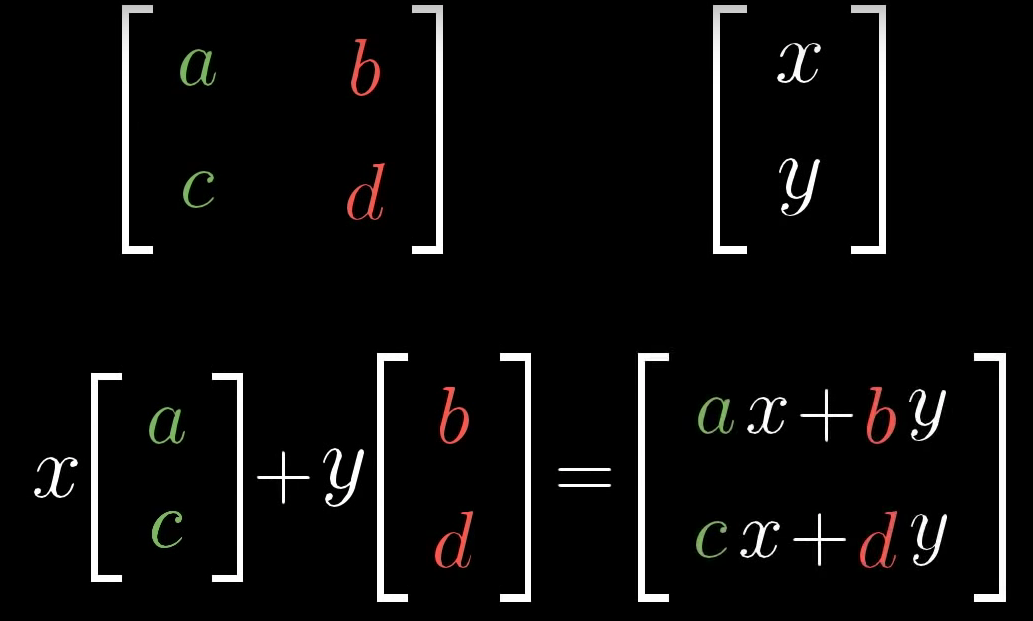
   $$ \mathbf{v} = \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \color{red} x \color{red} {\underbrace{\begin{bmatrix} 1 \\ 0 \end{bmatrix}}_ {\hat{i}}} + \color{red} y \color{red} {\underbrace{\begin{bmatrix} 0 \\ 1 \end{bmatrix}}_ {\hat{j}}} = \begin{bmatrix} 1\times x + 0 \times y \\ 0\times x + 1 \times y \end{bmatrix} = x\hat{i} + y\hat{j} $$

   The Matrix-Vector Product:
   

   Non-Square Matrices \((N \times M)\):
   Map vectors from \(\mathbb{R}^M \rightarrow \mathbb{R}^N\).
   They are transformations between dimensions.

7. The Product of Two Matrices:
   The Product of Two Matrices Corresponds to the composition of the transformations, being applied from right to left.
   This is very important intuition:

   e.g. do matrices commute?
   if you think of the matrices as transformations of space then answer quickly is no.
   Equivalently, Are matrices associative? Yes, function composition is associative: \(f \circ(g \circ h) = (f \circ g) \circ h\)

   

   E.g. Applying two transformations, a Rotation and a Shear:
   Instead of computing the Matrix-Vector product first, then another Matrix-Vector product on the resulting vector, we can combine/compose the two transformations/matrices into one new composition matrix that specifies the new coordinates after applying the two transformations:
   
   where the composition matrix is the Product of the two matrices:
   

   Matrix Multiplication (Composition) Explained

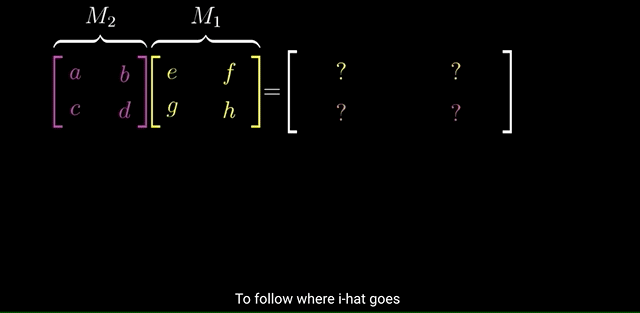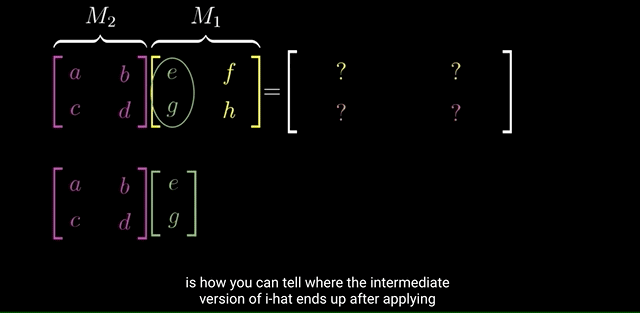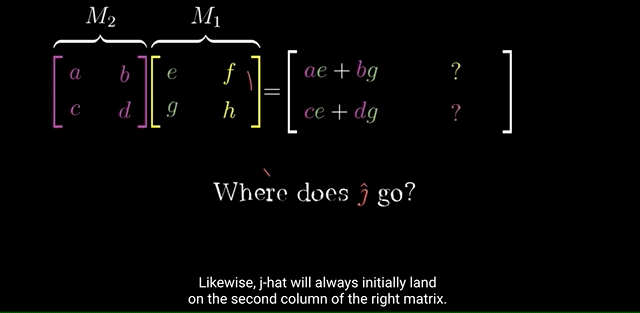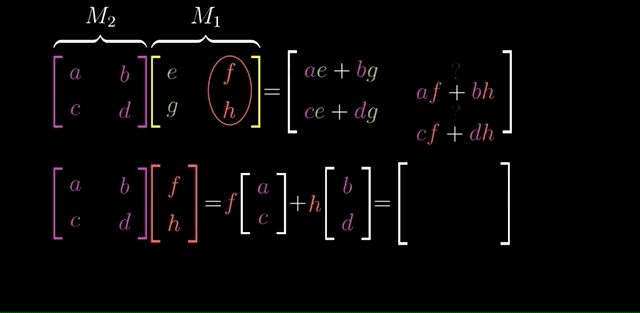
8. Linear Transformations:
   Linear Transformations are transformations that preserve the following properties:
   1. All vectors that are parallel remain parallel
   2. All vectors are evenly spaced
   3. The origin remains fixed
   • An Equivalent Definition of Linearity

   Visualization:

   • Examples of NON-linear Transformations:
     Breaks first rule

     Breaks second rule

     Breaks first rule but only on diagonal lines

   • The new coordinates of the basis vectors \(\hat{\imath}, \hat{\jmath}\) allow us to deduce where every vector is going to land after the transformation, by deducing the linear transformation/function on each basis vector.
     So, if a vector \(\overrightarrow{\mathbf{v}}\) - defined as some linear combination of \(\hat{\imath}, \hat{\jmath}\):

     $$\overrightarrow{\mathbf{v}}=a \hat{\imath}+b \hat{\jmath}$$

     undergoes a linear transformation, it is now defined as the exact same linear combination of the transformed coordinates of \(\hat{\imath}, \hat{\jmath}\):

     $$\text { Transformed } \overrightarrow{\mathbf{v}}=a(\text { Transformed } \hat{\imath})+b(\text { Transformed } \hat{\jmath})$$

   • We tend to combine the two basis vectors in a matrix side by side.

     $$\begin{bmatrix} \hat{\imath} & \hat{\jmath} \end{bmatrix}$$

     E.g. in 2D:

     $$\begin{bmatrix} 1 & 0 0 & 1 \end{bmatrix}$$

     and after a certain linear transformation, the new coordinates of the basis vectors define the new matrix:

   Notes:

   • You should interpret a matrix as a linear transformation of space
   • Each column represents where the corresponding basis vector lands
   • To Transform any vector to the new, linearly transformed space, you can multiply the matrix and the vector to get the new coordinates of the vector in that space
   • A Linear Transformation corresponds to Matrix-Vector multiplication
     • Each coordinate of your vector, scales the corresponding basis vector (column) in the new space
   • We only need to know the coordinates of the basis vectors in the new space to specify a linear transformation
     
     

9. The Determinant:
   The Determinant of a transformation is the “scaling factor” by which the transformation changed any area in the vector space.

   The Negative Determinant determines the orientation.

   Linearity of the Determinant:

   $$\text{det}(AB) = \text{det}(A) \text{det}(B)$$

10. Solving Systems of Equations:
    The Equation \(A\mathbf{x} = \mathbf{b}\), finds the vector \(\mathbf{x}\) that lands on the vector \(\mathbf{b}\) when the transformation \(A\) is applied to it.

    Again, the intuition: is to think of a linear system of equations, geometrically, as trying to find a particular vector that once transformed/moved, lands on the output vector \(\mathbf{b}\).

    • This becomes more important when you think of the different properties, of that transformation/function, encoded (now) in the matrix \(A\):
      • When the \(det(A) \neq 0\) we know that space is preserved, and from the properties of linearity, we know there will always be one (unique) vector that would land on \(\mathbf{b}\) once transformed (and you can find it by “playing the transformation in reverse” i.e. the inverse matrix).
      • When \(det(A) = 0\) then the space is squished down to a lower representation, resulting in information loss.

    Usefullness of LA:

    Linear System of Equations:
    
    Linear System of Equations

    • Intuition:
      • The Matrix \(A\) is a Linear Transformation
      • Solving the Equation \(A \overrightarrow{\mathrm{x}}=\overrightarrow{\mathrm{v}}\) means:
        We are looking for a vector \(\mathrm{x}\) which - after applying the linear transformation \(A\) - lands on \(\mathrm{v}\).

      Visualization

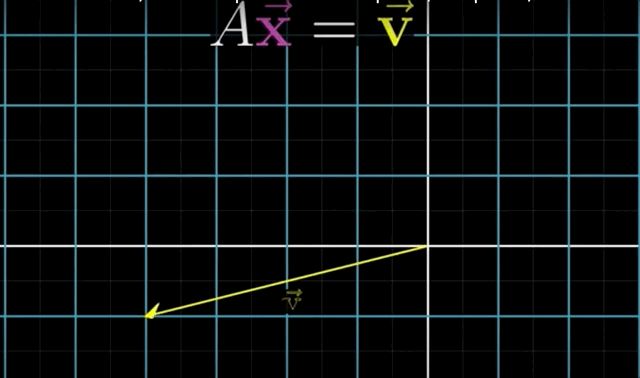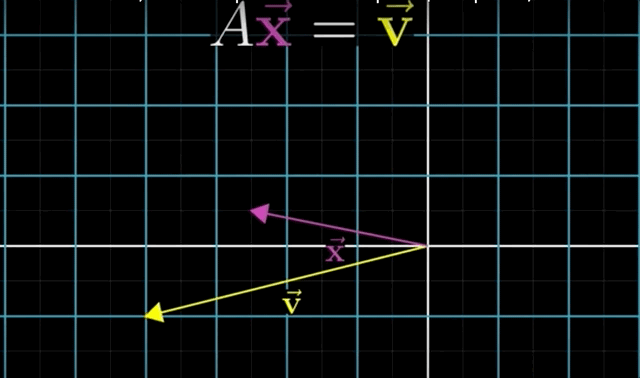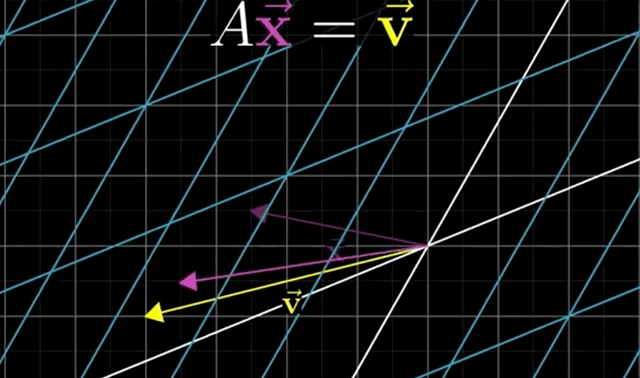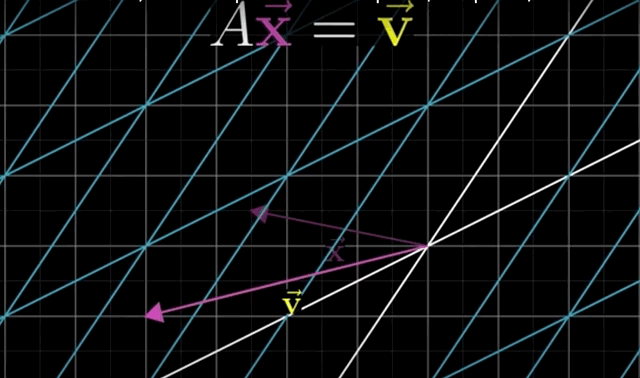
      • Key Insight: you can understand the system of linear equations of \(n\) variables by thinking of transforming space and figuring out which vector lands on another!

      Insight

11. The Inverse of a matrix:
    The Inverse of a matrix is the matrix such that if we “algebraically” multiply the two matrices, we get back to the original coordinates (the identity).
    It is, basically, the transformation applied in reverse.

    The Inverse Matrix is the unique matrix/transformation such that:

    $$A^{-1} A = I$$

    Why inverse transformation/matrix DNE when the __det__erminant is Zero (i.e. space is squished):
    To do so, is equivalent to transforming a line into a plane, which would require mapping each, individual, vector into a “whole line full of vectors” (multiple vectors); which is not something a Function can do.
    Functions map single input to single output.

    • Solution when the Determinant is Zero: It is still possible that a solution exists even when the Determinant is Zero.
      This happens in the (lucky) case that the vector \(\mathrm{v}\) (on the RHS) “lives” on the line (squashed space):
      
      Note: the green and red vectors are the transformed basis vectors.

      • This becomes more and more unlikely as the Rank of the output gets lower
        e.g. Squashing a 3D space on a line (Rank=1)
12. The Determinants, Inverses, & Solutions to Equations:
    When the \(\text{det} = 0\) the area gets squashed to \(0\), and information is lost. Thus:
    1. The Inverse DNE
    2. A unique solution DNE

       i.e. there is no function that can take a line onto a plane; info loss

13. The Rank:
    The Rank is the dimensionality of the output of a transformation.
    More precisely, it is the number of dimensions in the column space.
    Viewed as a Matrix, it is the number of independent vectors (as columns) that make up the matrix.

14. The Column Space:
    The Column Space is the set of all possible outputs of a transformation/matrix.
    • View each column as a basis vector; there span is then, all the possible outputs
    • The Zero Vector (origin): is always in the column space (corresponds to preserving the origin)

    The Column Space allows us to understand when a solution exists.
    For example, even when the matrix is not full-rank (det=0) a solution might still exist; if, when \(A\) squishes space onto a line, the vector \(\mathbf{b}\) lies on that line (in the span of that line).

    • Formally, solution exists if \(\mathbf{b}\) is in the column space of \(A\).

15. The Null Space:
    The Null Space is the set of vectors that get mapped to the origin; also known as The Kernel.

    The Null Space allows us to understand what the set of all possible solutions look like.

    When the vector \(\mathrm{v} = \mathrm{0}\), the null space gives all the possible solutions to the equation \(A \overrightarrow{\mathrm{x}}=\overrightarrow{\mathbf{v}} = 0\)

    Rank and the Zero Vector:
    A Full-Rank matrix maps only the origin to itself.
    A non-full rank (det=0) (rank=n-1) matrix maps a whole line to the origin, (rank=n-2) a plane to the origin, etc.

16. Non-Square Matrices:{: style=”color: SteelBlue”}{: .bodyContents1 #bodyContents1144}
    If the matrix has shape \(m \times n\) and \(m > n\), then it can be viewed as transforming an \(n\)-dimensional vector to \(m\)-dimensional space. (e.g. a line to a plane)

    When \(m < n\) then it is taking your vector from a lower dimension to a higher dimension.

    Some Extra Intuition:
    Intuition

17. The Dot Product/Scalar Product:
    (for vectors \(\mathbf{u}, \mathbf{v}\))

    $$\mathbf{u} \cdot \mathbf{v} = \mathbf{u}^T \mathbf{v}$$

    • Geometrically:
      1. project
18. Cramer’s Rule:
    • Cramer’s Rule Geometrically

19. Coordinate Systems:

    A Coordinate System is just a way to formalize the basis vectors and their lengths. All coordinate systems agree on where the origin is.
    Coordinate Systems are a way to translate between vectors (defined w.r.t. basis vectors being scaled and added in space) and sets of numbers (the elements of the vector/list/array of numbers which we define).

    • Translating between Coordinate Systems

      Imp: 6:47

    • Translating a Matrix/Transformation between Coordinate Systems

    Implicit Assumptions in a Coordinate System:

    • Direction of each basis vector our vector is scaling
    • The unit of distance

20. Eigenstuff:

    • Computing the Eigenvalues/vectors Intuition
    • Diagonalization

    Notes:

    • Complex Eigenvalues, generally, correspond to some kind of rotation in the transformation/matrix (think, multiplication by \(i\) in \(\mathbb{C}\) is a \(90^{\deg}\) rotation).
    • For a diagonal matrix, all the basis vectors are eigenvectors and the diagonal entries are their eigenvalues.