Limits and Continuity

1. Limit [of Function]:
   

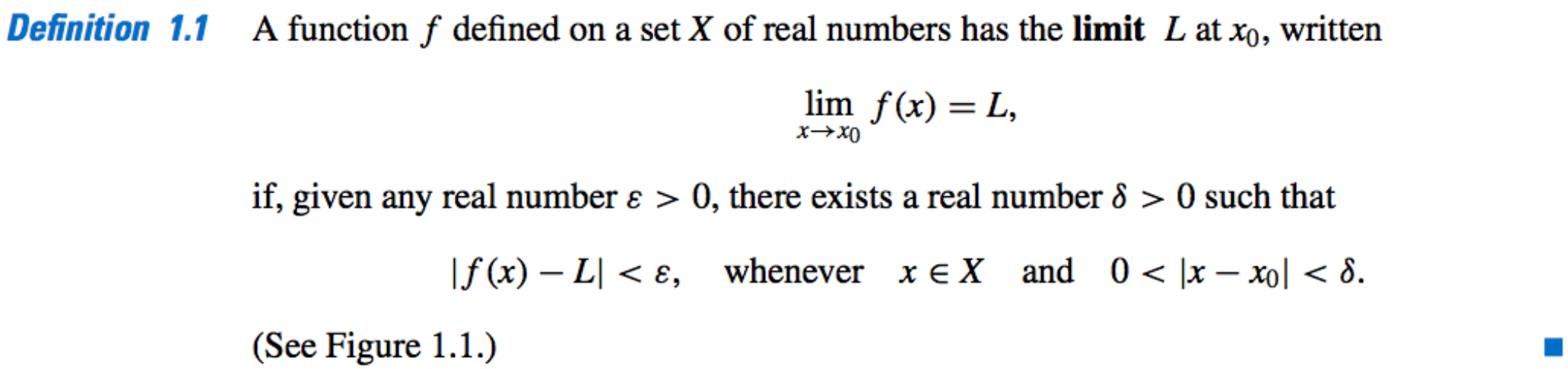
2. Continuity:
   

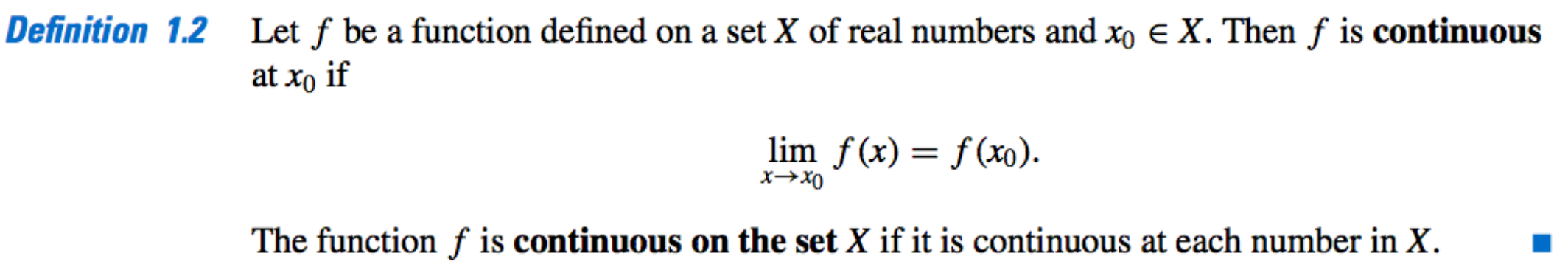
3. Limit [of Sequence]:
   

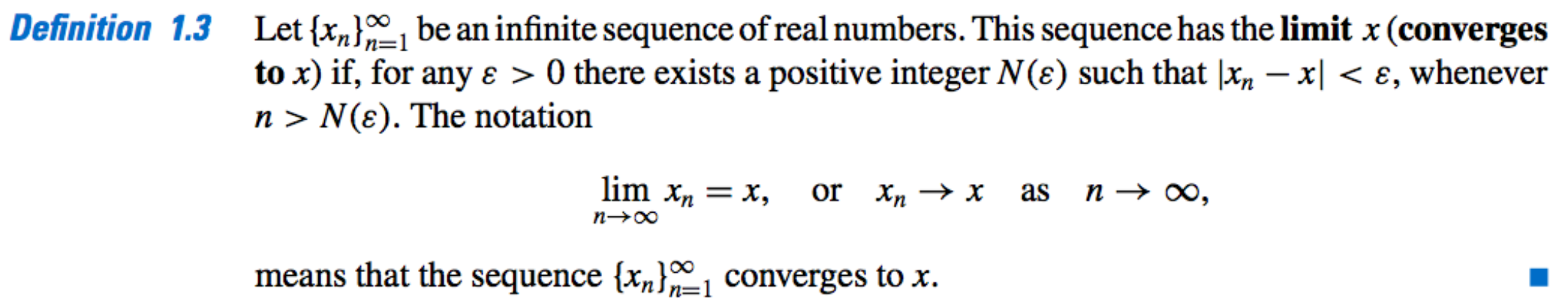
4. Convergence and Continuity, Correspondance:
   

Differentiability

1. Differentiablity:
   

2. Differentiablity and Continuity, Correspondance:
   

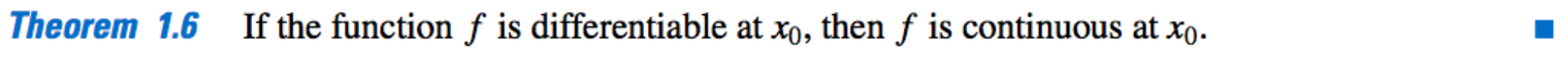
3. Rolle’s Theorem:
   

4. Generalized Rolle’s Theorem:
   

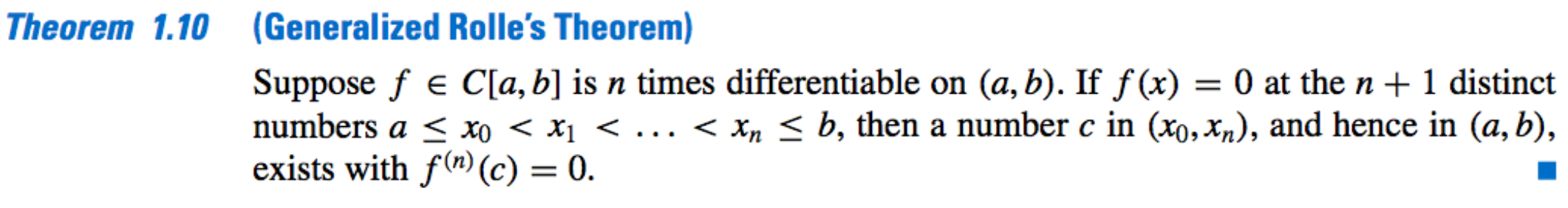
5. Mean Value Theorem:
   

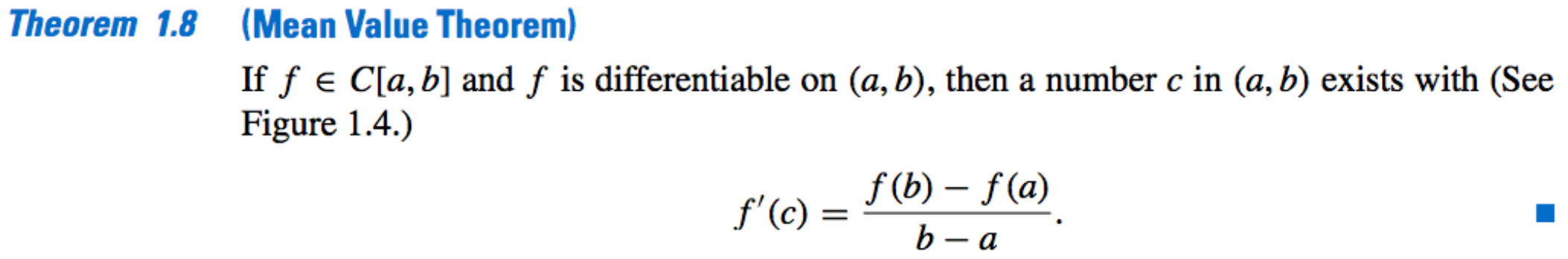
   Proof.
   \(\begin{align} &\ f(a) = g(a)\ \ \ \ \ \\ & \ f(b) = g(b) \\ & \ h(x) = f(x) - g(x)\ \text{, [define }h(x)] \\ & \iff h(a) = h(b) = 0 \\ & \implies h'(x) = f'(x) - g'(x)\\ & \implies h'(x) = f'(x) - g'(x) = 0, \ \ \text{[for some } x = c]\\ & \implies f'(c) = g'(c) = \dfrac{g(b) - g(a)}{b-a}\\ & \implies f'(x) = \dfrac{f(b) - f(a)}{b-a} \end{align}\)

6. Extreme Value Theorem:
   

7. Intermediate Value Theorem:
   

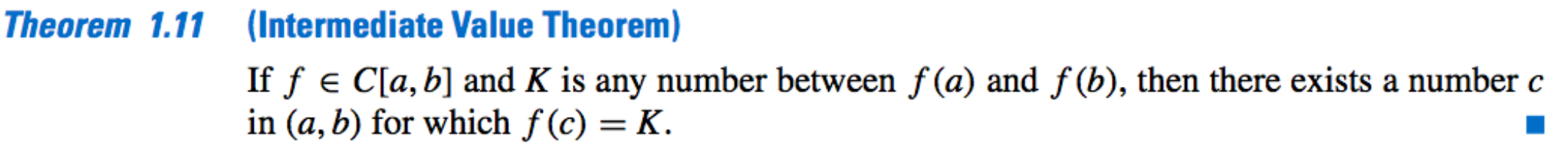
Integration

1. The Riemann Integral:
   

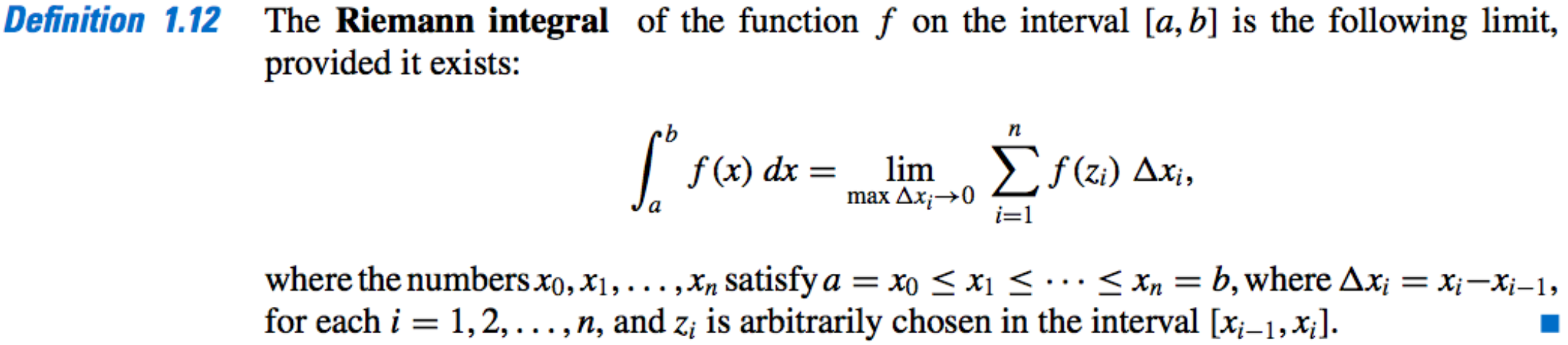
   Or, for equally spaced intervals,
   

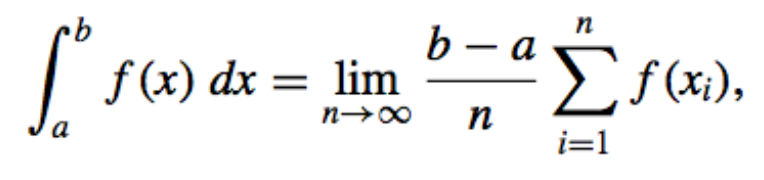
2. Integrability and Continuity, Correspondance:

   A function f that is continuous on an interval \([a, b]\) is also Riemann integrable on \([a, b]\)

3. Weighted Mean Value Theorem for Integrals:
   

   When \(g(x) ≡ 1\), Theorem 1.13 is the usual Mean Value Theorem for Integrals.
   It gives the average value of the function \(f\) over the interval \([a, b]\)
   \(f(c)\ = \ \dfrac{1}{b − a} \int_a^b f(x) \ dx.\)

Taylor Polynomials and Series

1. Taylor’s Theorem:
   

   \(P_n(x)\): is called the nth Taylor polynomial for \(f\) about \(x_0\).

   \(R_n(x)\): is called the truncation error (or remainder term) associated with \(P_n(x)\).

   Since the number \(ξ(x)\) in the truncation error \(R_n(x)\) depends on the value of x at which the polynomial \(P_n(x)\) is being evaluated, it is a function of the variable \(x\).

   Taylor’s Theorem, only, ensures that such a function \((ξ(x))\) exists, and that its value lies between \(x\) and \(x_0\), and not how to determine the function \((ξ(x))\).

2. Polynomials:
   
   • Taylor’s Polynomial: The polynomial definied by
     
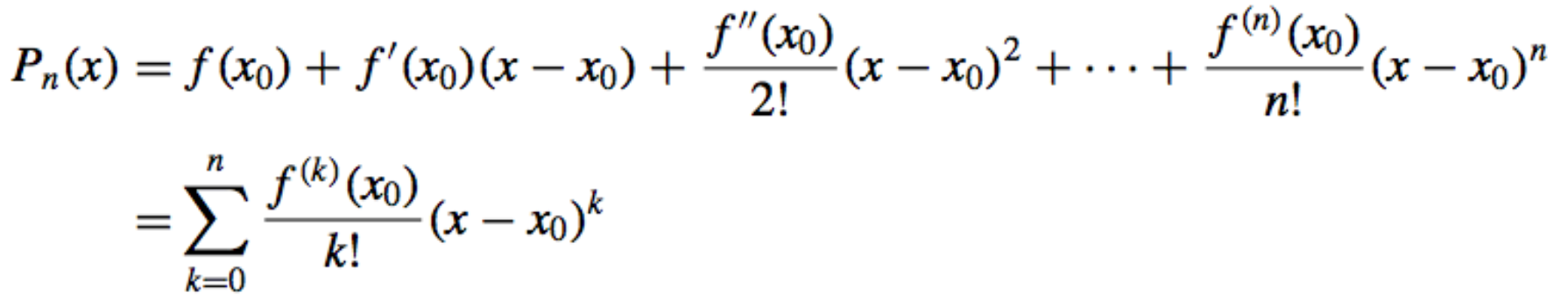
   • Maclaurin Polynomial: The special case Taylors Polynomial with \(x_0 = 0\).
3. Series:
   
   • Taylor’s Series: The infinite series obtained by taking the limit of \(P_n(x),\text{as }\ n \rightarrow \inf\).
   • Maclaurin Series: The special case Taylors series with \(x_0 = 0\).

4. Truncation Error:

   Refers to the error involved in using a truncated, or finite, summation to approximate
   the sum of an infinite series.