Binary Machine Numbers

1. Representing Real Numbers:

   A 64-bit (binary digit) representation is used for a real number.

   • The first bit is a sign indicator, denoted \(s\).
   • Followed by an 11-bit exponent, \(c\), called the characteristic,
   • and a 52-bit binary fraction, \(f\) , called the mantissa.
   • The base for the exponent is 2.

2. Floating-Point Number Form:

   \[(−1)^s\ \ 2^{c−1023} \ (1 + f)\]

3. Smallest Normalized positive Number:

   When: \(s = 0, \ \ c = 1,\ \\) and \(\ \ f = 0\).
   Equivalent to: \(2^{−1022}\ \ \dot \ \ (1 + 0) \ \approx \ 0.22251 \ \dot \ 10^{−307}\).

4. Largest Normalized positive Number:
   

   When: \(s = 0,\ \ c = 2046,\ \\) and \(\ \ f = 1 - 2^{-52}\).
   Equivalent to: \(2^{1023}\ \dot \ (2 - 2^{-52}) \ \approx 0.17977 × 10^{309}\).

5. UnderFlow:

   When numbers occurring in calculations have a magnitude less than,
   \(2^{-1022}\).

6. OverFlow:

   When numbers occurring in calculations have a magnitude greater than,
   \(2^{1023} \dot (2 - 2^{-52})\).

7. Representing the Zero:
   
   • There are Two Representations of the number zero:
     1. A positive 0: when \(s = 0, \ \ c = 0, \ \\) and \(\ f = 0\).
     2. A negative 0: when \(s = 1, \ \ c = 0, \ \\) and \(\ f = 0\).

Decimal Machine Numbers

1. What?

   We assume that machine numbers are represented in the normalized decimal floating-point form.

2. (k-digit) Decimal Machine Numbers:

   \[±0.d_1d_2 ... d_k × 10^n , 1 \leq d_1 \leq 9, \text{and } 0 \leq d_i \leq 9,\]

   \(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{for each } i = 2, ... , k\).

3. Normalized Form:

   \[y = 0.d_1d_2 ... d_k × 10^n\]

4. Floating-Point Form of a Decimal Machine Number:
   The floating-point form of y, denoted \(f_l(y)\), is obtained by terminating the mantissa of \(y\) at k-decimal digits.
5. Termination:
   There are two common ways of performing this termination:
   • Chopping: is to simply chop off the digits \(d_{k+1}d_{k+2}\).

     This produces the floating-point form: \(f_l(y) = 0.d_1d_2 ... d_k × 10^n\)

   • Rounding: adds \(5 × 10^{n−(k+1)}\) to \(y\) and then chops the result

     This produces the floating-point form: \(f_l(y) = 0.\delta_1\delta_2 ... \delta_k × 10^n\).

     For rounding, when \(d_{k+1} \geq 5\), we add \(1\) to \(d_k\) to obtain \(f_l(y)\); that is, we round up. When \(d_{k+1} < 5\), we simply chop off all but the first k digits; so we round down. If we round down, then \(\delta_i = d_i\), for each \(i = 1, 2, ... , k\).
     However, if we round up, the digits (and even the exponent) might change.

6. Approximation Errors:
   

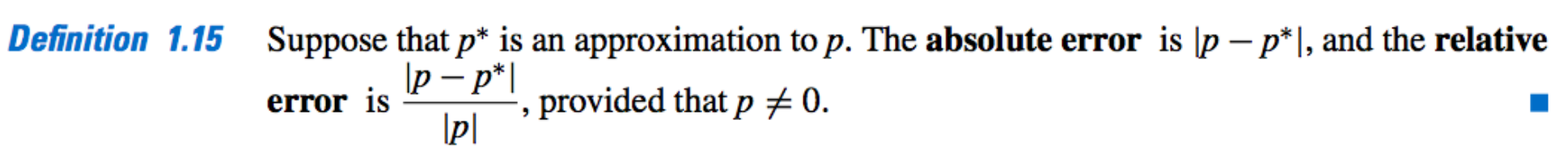
   • The Absolute Error: \(\ \ \ \ \ \ \ \|p − p^∗\|\).

   • The Relative Error: \(\ \ \ \ \ \ \ \dfrac{\|p − p^∗\|}{\|p\|}\).

7. Significant Digits:
   

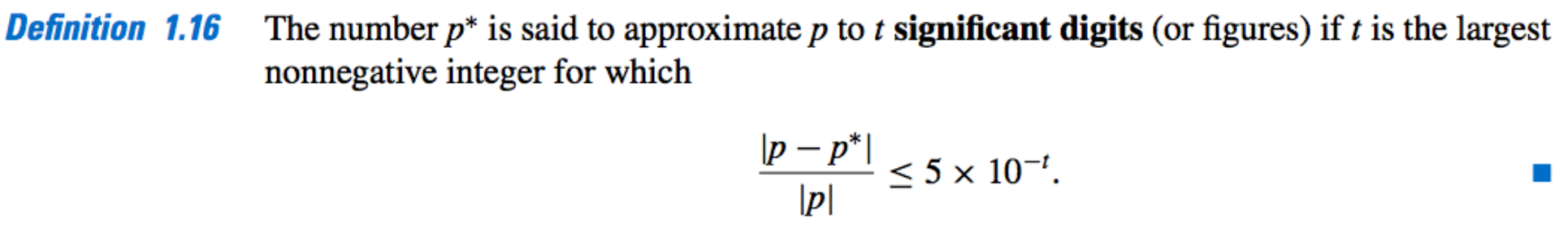
8. Error in using Floating-Point Repr.:
   

   • Chopping:

     The Relative Error = \(|\dfrac{y - f_l(y)}{y}|\)

     The Machine Repr. [for k decimial digits] =

     \(y = 0.d_1d_2 ... d_kd_{k+1} ... × 10^n\).

     \(\implies\)
     
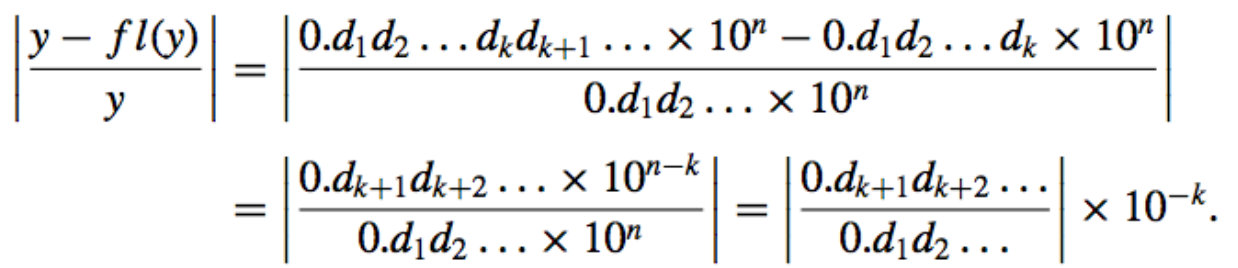
     Bound \(\ \ \ \implies \ \ |\dfrac{y - f_l(y)}{y}| \leq \dfrac{1}{0.1} \times 10^{-k} = 10^{-k+1}\).

   • Rounding:

     In a similar manner, a bound for the relative error when using k-digit rounding arithmetic is

     Bound \(\ \ \ \implies \ \ \|\dfrac{y - f_l(y)}{y}\| \leq 0.5 × 10^{−k+1}\).

9. Distribution of Numbers:
   The number of decimal machine numbers in \([10^n, 10^{n+1}]\) is constant for all integers \(n\).

Finite-Digit Arithmetic

1. Values:

   \[x = f_l(x) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)\]

   \[y = f_l(y) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2)\]

2. Operations:
   
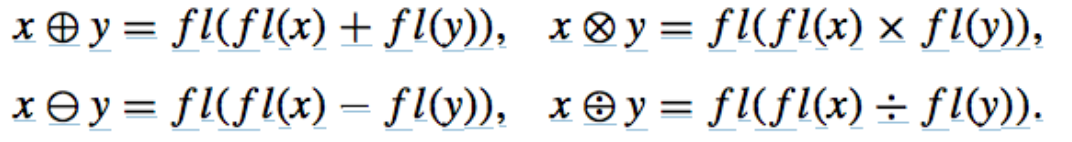
3. Error-producing Calculations:
   
   • Cancelation of significant digits due to the subtraction of nearly equal numbers.
     Show Error
   • Dividing by a number with small magnitude / Multiplying by a number with large magnitude.
     Show Error
4. Avoiding Round-Off Error:
   

   The loss of accuracy due to round-off error can often be avoided by a reformulation of the calculations.

   We change the form of the quadratic formula by rationalizing the numerator:
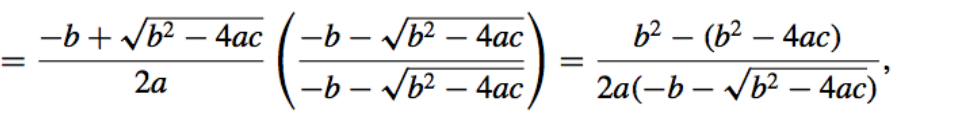
   \(\implies \ \ \ \ \ \ \ \ \ \ \ \ \ \ x_1 = \dfrac{−2c}{b + \sqrt{b^2 − 4ac}}, \ \ \ \ \ \ \ \ \ \ \ \ \ \ x_2 = \dfrac{−2c}{b - \sqrt{b^2 − 4ac}},\)

Nested Arithmetic

1. What?

   Rearranging calculations to reduce the number of computations.

   Remember that chopping (or rounding) is performed after each calculation.

   Polynomials should always be expressed in nested form before performing an evaluation, because this form minimizes the number of arithmetic calculations.

2. Why?

   Accuracy loss due to round-off error can also be reduced by rearranging calculations to reduce the number of computations.