Fixed-Point Problems

1. Fixed Point:

   A fixed point for a function is a number at which the value of the function does not change when the function is applied.

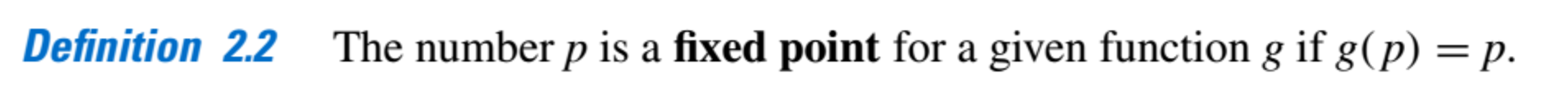
2. Root-finding problems and Fixed-point problems:
   

   Root Finding and Fixed-point problems are equivalent in the following sense

   

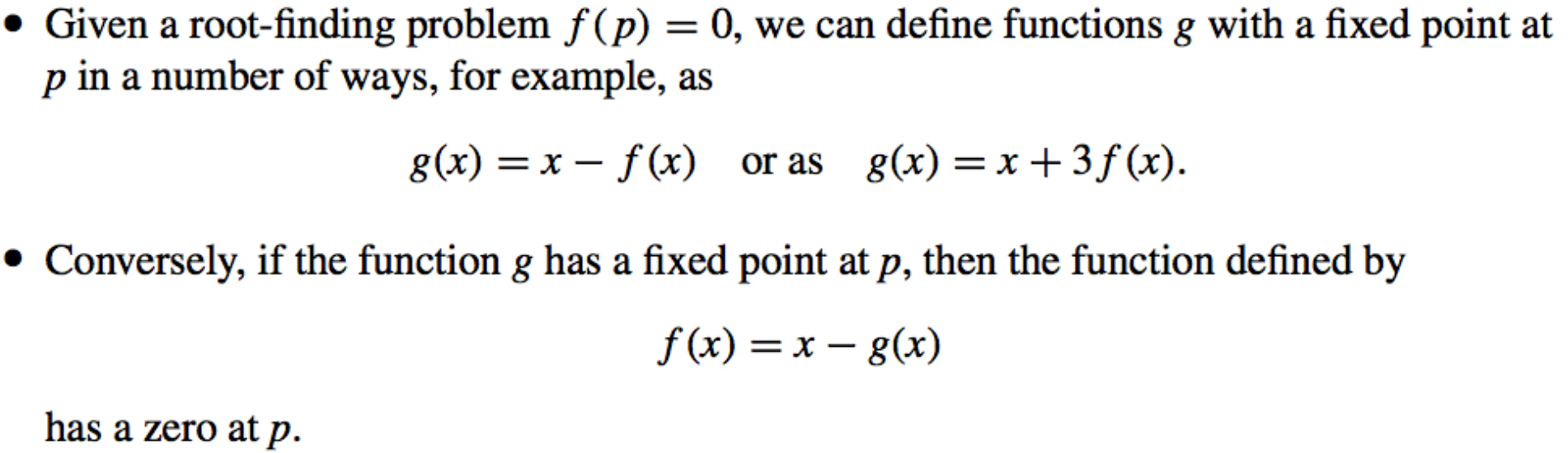
3. Why?:
   Although the problems we wish to solve are in the root-finding form, the fixed-point form is easier to analyze, and certain fixed-point choices lead to very powerful root-finding techniques.

4. Existence and Uniqueness of a Fixed Point.:
   

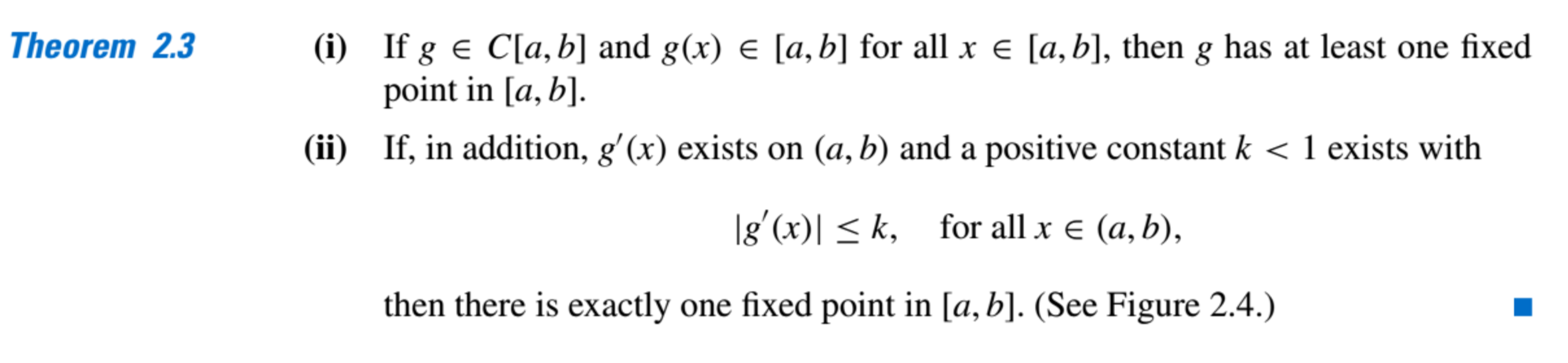
Fixed-Point Iteration

1. Approximating Fixed-Points:
   

2. Algorithm:
   

3. Convergence:
   • Fixed-Point Theorem:
     

   • Error bound in using \(p_n\) for \(p\):
     

     Notice:
     The rate of convergence depends on the factor \(k^n\). The smaller the value of \(k\), the faster the convergence, which may be very slow if \(k\) is close to 1.

4. Using Fixed-Points:
   

   Question. How can we find a fixed-point problem that produces a sequence that reliably and rapidly converges to a solution to a given root-finding problem?

   Answer. Manipulate the root-finding problem into a fixed point problem that satisfies the conditions of Fixed-Point Theorem 2.4 and has a derivative that is as small as possible near the fixed point.

5. Newton’s Method as a Fixed-Point Problem:
   

6. Convergence Example:
   Show Example

7. MatLab Implementation: