Table of Contents
Newton’s Method
- What?:
- Newton’s (or the Newton-Raphson) method is one of the most powerful and well-known numerical methods for solving a root-finding problem
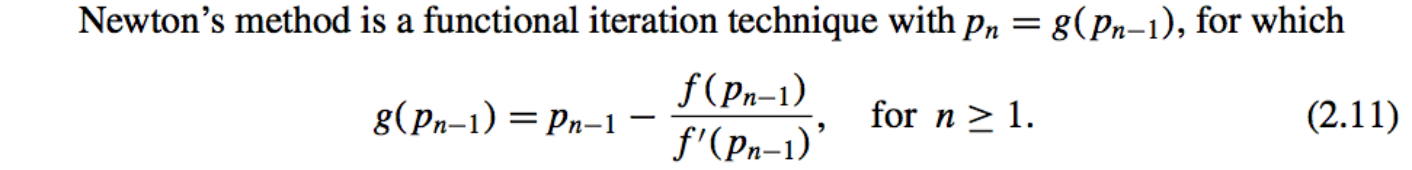

-
Derivation:
Derivation can be found here -
Algorithm:

-
Stopping Criterions:
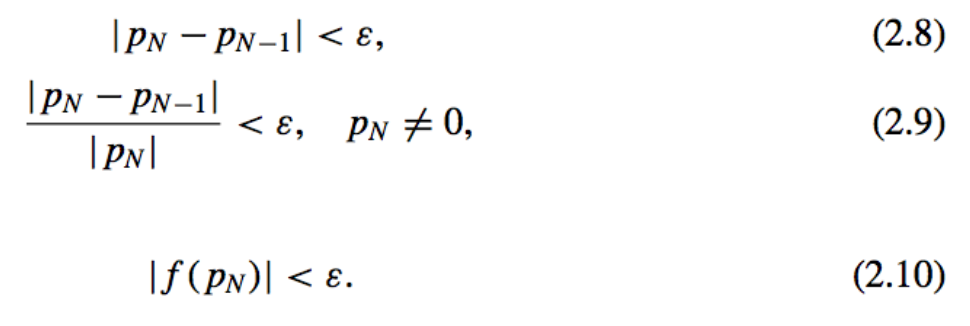
- MatLab Implementation:

Convergence using Newton’s Method
- Convergence Theorem:
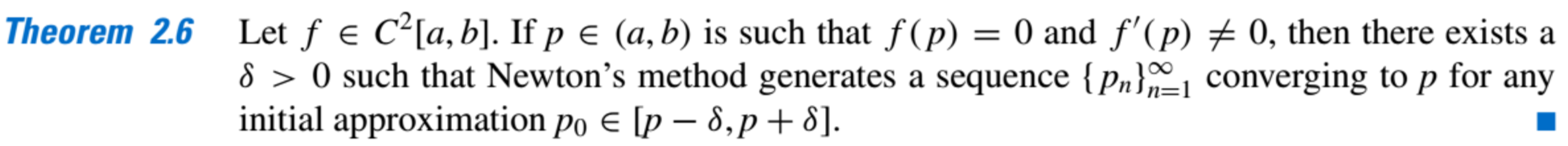
The crucial assumption is that the term involving \(( p − p_0)^2\) is, by comparison with \(| p − p_0|\), so small that it can be deleted
Theorem 2.6 states that,
(1) Under reasonable assumptions, Newton’s method converges provided a sufficiently accurate initial approximation is chosen.
(2) It also implies that the constant k that bounds the derivative of g, and, consequently, indicates, the speed of convergence of the method, decreases to 0 as the procedure continues.
The Secant Method
-
What?
In Newton’s Method
We approximate \(f'( p_n−1)\) as:

To produce:

- Why?
Newton’s Method Weakness: the need to know the value of the derivative of f at each approximation.
Frequently, \(f'(x)\) is harder and needs more arithmetic operations to calculate than \(f(x)\).
Note: only one function evaluation is needed per step for the Secant method after \(p_2\) has been determined. In contrast, each step of Newton’s method requires an evaluation of both the function and its derivative.
-
Algorithm:

- Convergence Speed:
Generally,
The convergence of the Secant method is much faster than functional iteration but slightly slower than Newton’s method.
The Method of False Position
-
What?
The method of False Position (also called Regula Falsi) generates approximations in the same manner as the Secant method, but it includes a test to ensure that the root is always bracketed between successive iterations. -
Why?
Root bracketing is not guaranteed for either Newton’s method or the Secant method. -
Method:

-
Algorithm:
