Aitken’s \(\Delta^2\) Method

1. What?
   

   Derivation can be found here!

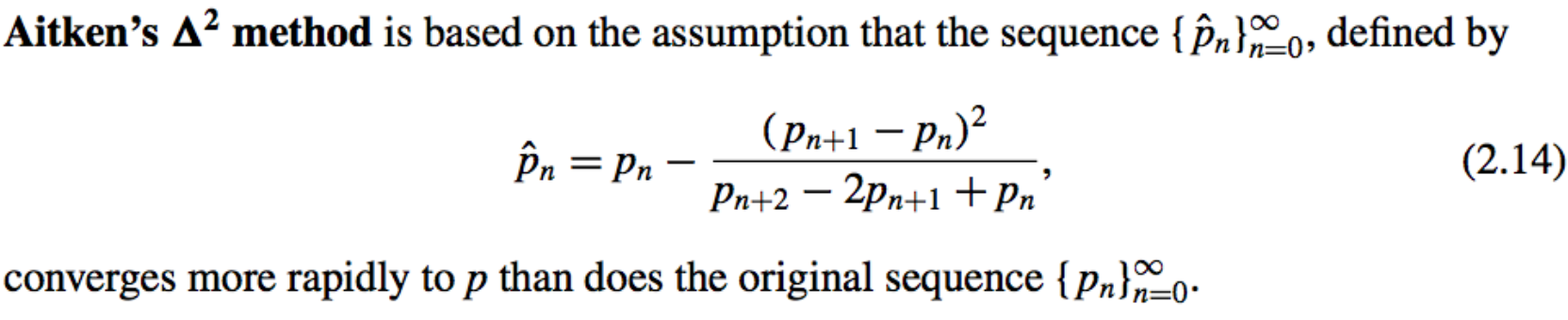
2. Why?
   Can be used to accelerate the convergence of a sequence that is linearly convergent, regardless of its origin or application.

3. Del [Forward Difference]:
   

4. \(\hat{p}_n\) [Formula]:
   

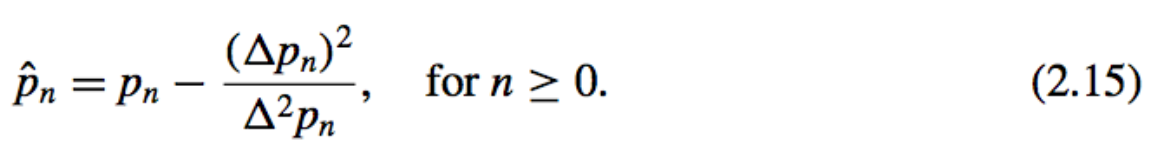
5. Generating the Sequence [Formula]:
   

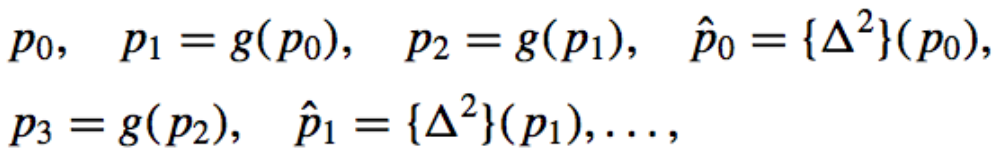
Steffensen’s Method

1. What?:

   By applying a modification of Aitken’s \(\Delta^2\) method to a linearly convergent
   sequence obtained from fixed-point iteration, we can accelerate the convergence to quadratic.

2. Zeros and their Multiplicity:
   

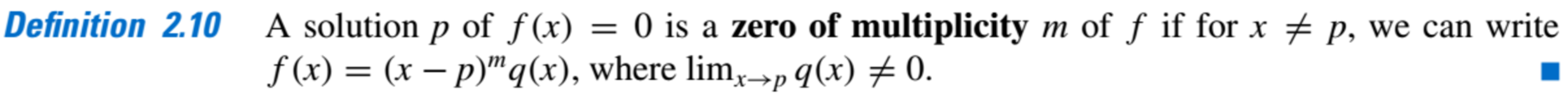
3. Difference from Aitken’s method:
   
   • Aitken’s method: Constructs the terms in order
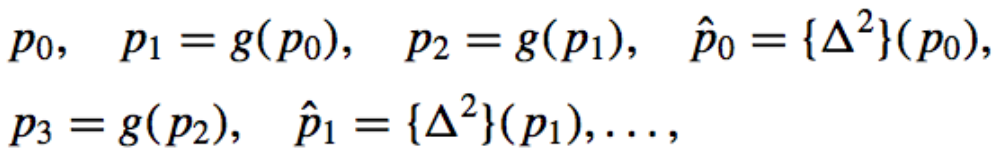
   • Steffensen’s method: constructs the same first four terms, \(p_0, p_1, p_2,\) and \(\hat{p}_0\). However, at this step we assume that \(\hat{p}_0\) is a better approximation to \(p\) than is \(p_2\) and apply fixed-point iteration to \(\hat{p}_0\) instead of \(p_2\)

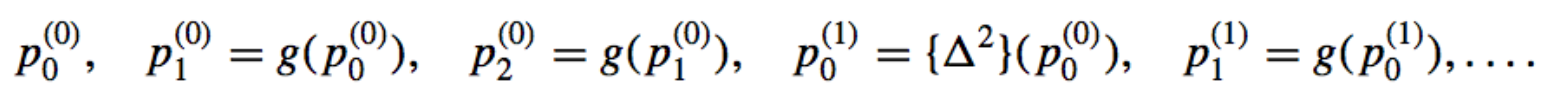
   Notice
   Every third term of the Steffensen sequence is generated by Eq. (2.15);
   the others use fixed-point iteration on the previous term.

4. Algorithm:
   Show Algorithm

5. Convergance of Steffensen’s Method:
   

   Steffensen’s Method gives quadratic convergence without evaluating a derivative.

6. MatLab Implementation: