Algebraic Polynomials

1. What?

   Set of Functions of the form:

   \[P_n(x) = a_nx^n + a_{n−1}x^{n−1} +···+ a_1x + a_0\]

2. Why?

   Polynomials uniformly approximate continuous functions. By this we mean that given any function, defined and continuous on a closed and bounded interval, there exists a polynomial that is as “close” to the given function as desired.

3. Weierstrass Approximation Theorem:
   )

   i.e. Polynomials uniformly approximate continuous functions.

4. Taylor Polynomials:
   

   Taylor Polynomials are generally bad at approximating functions anywhere but at a certain point \(x_0\). To approximate an interval, we do not use Taylors Polynomials.

Lagrange Interpolating Polynomials

1. The linear Lagrange interpolating polynomial:
   

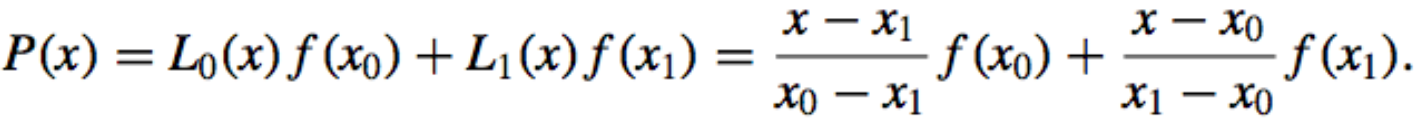
2. The nth Lagrange interpolating polynomial:
   

3. The error term (bound):
   

   PROOF