Table of Contents

Neville’s Method

  1. What?
    A recursive method definition used to generate successively higher-degree
    polynomial approximations at a specific point.
  2. Why?
    A practical difficulty with Lagrange interpolation is that the error term is
    difficult to apply, so the degree of the polynomial needed for the desired accuracy is generally not known until computations have been performed.
  3. The lagrange Polynomial of the point \(x_{m_i}\):
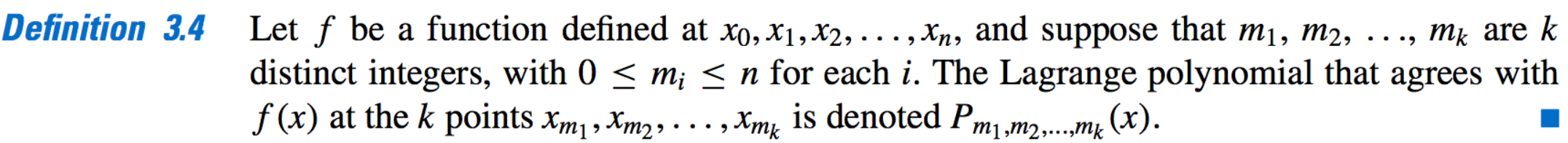
    definition
  4. Method to recursively generate Lagrange polynomial:
    • Method:
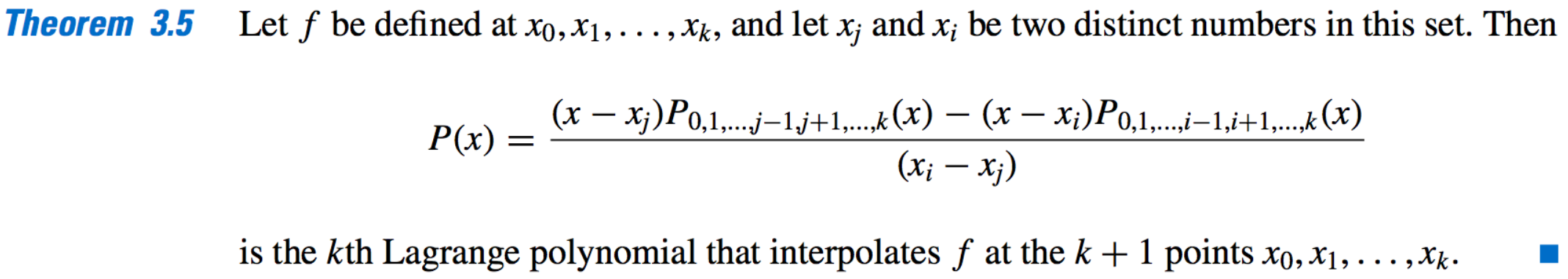
      definition
    • Examples: \(P_{0,1} = \dfrac{1}{x_1 − x_0}[(x − x_0)P_1 − (x − x_1)P_0], \\ P_{1,2} = \dfrac{1}{x_2 − x_1}[(x − x_1)P_2 − (x − x_2)P_1], \\ P_{0,1,2} = \dfrac{1}{x_2 − x_0}[(x − x_0)P_{1,2} − (x − x_2)P_{0,1}]\)
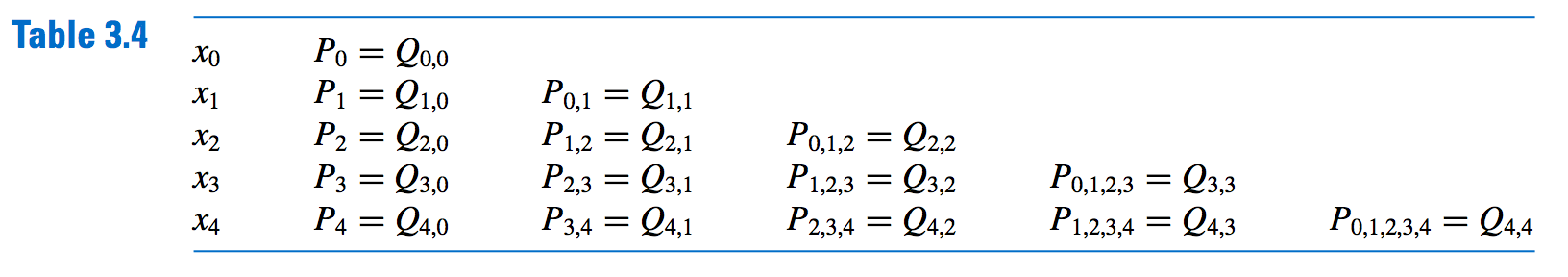
    • Generated according to the following Table: Table
  5. Notation and subscripts:

    • Proceeding down the table corresponds to using consecutive points \(x_i\) with larger i, and proceeding to the right corresponds to increasing the degree of the interpolating polynomial.

    • To avoid the multiple subscripts, we let \(Q_{i,j}(x),\) for \(0 ≤ j ≤ i,\) denote the interpolating polynomial of degree j on the (j + 1) numbers \(x_{i−j}, x_{i−j+1}, ... , x_{i−1}, x_i\); that is,
      \[Q_{i,j} = P_{i−j},_{i−j+1},...,_{i−1},_i\]
  6. Algorithm:
    Nevilles Method
  7. Stopping Criterion:
    • Criterion:
      \(|Q_{i,i} − Q_{i−1,i−1}| < \epsilon\)
    • If the inequality is true, \(Q_{i,i}\) is a reasonable approximation to \(f(x)\).
    • If the inequality is false, a new interpolation point, \(x_{i+1}\), is added.
  8. OMG:
    \(P_{j,..,i} = \dfrac{1}{x_i − x_j}[(x − x_j)P_{j+1,..,i} − (x − x_i)P_{j,..,i-1}], \\ Q_{i,j} = \dfrac{1}{x_{i} − x_{i-j}}[(x − x_{i-j})Q_{i,j-1} − (x − x_i)Q_{i-1,j-1}], \\\)