Ahmad Badary

The derivative

Derivative:
\(f'(x_0) = \lim_{h\to\infty} \ \ \dfrac{f(x_0 + h) − f(x_0)}{h}\)
The forward/backward difference formula:

Derivative formulat [at \(x = x_0\)]
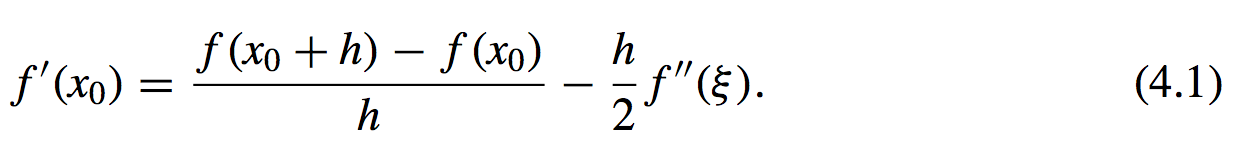
This formula is known as the forward-difference formula if \(h > 0\) and the backward-difference formula if \(h < 0\).

Error Bound: For small values of h, the difference quotient \(\dfrac{f(x_0 + h) − f(x_0)}{h}\) can be used to approximate \(f(x_0)\) with an error bounded by \(M\dfrac{|h|}{2}\), where \(M\) is a bound on \(|f''(x)|\) for \(x\) between \(x_0\) and \(x_0 + h\).
The \((n + 1)\)-point formula to approximate \(f'(x_j)\):
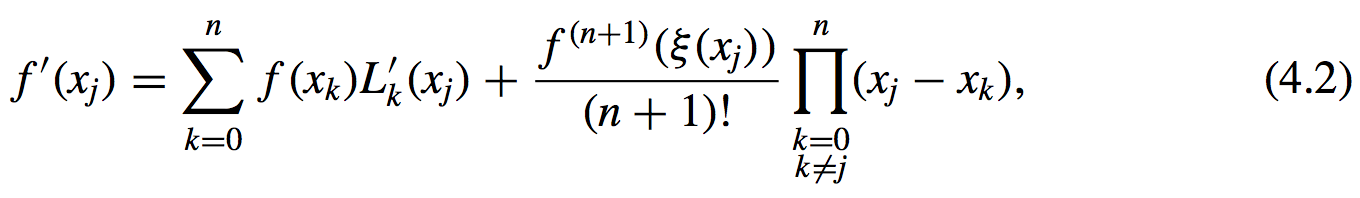
- Derivation:
Three-point Formula:

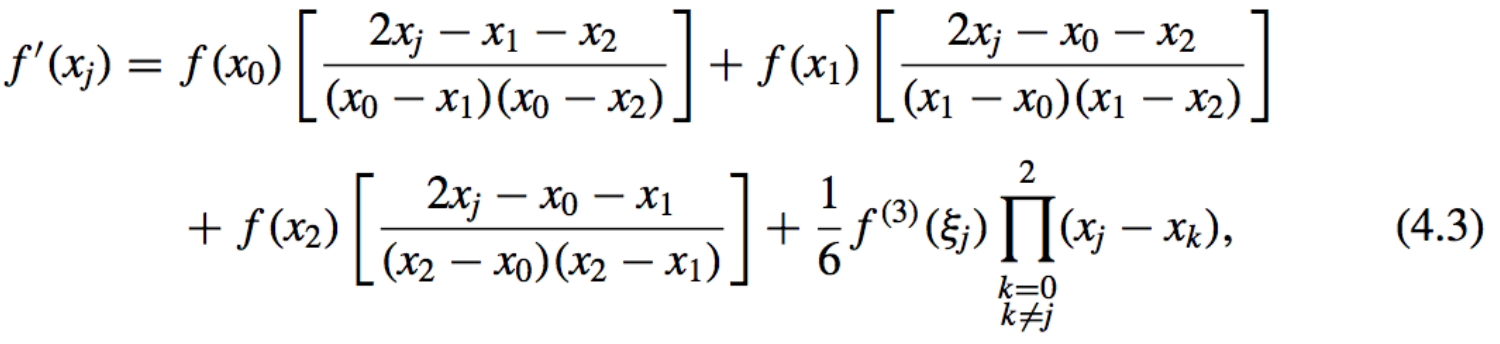
for each \(j = 0, 1, 2\), where the notation \(\zeta_j\) indicates that this point depends on \(x_j\).
- Derivation:

Equally Spaced nodes:

The formulas from Eq. (4.3) become especially useful if the nodes are equally spaced, that is, when \(x_1 = x_0 + h\) and \(x_2 = x_0 + 2h\), for some \(h \neq 0\).
We will assume equally-spaced nodes throughout the remainder of this section.
Three-Point Endpoint Formula:

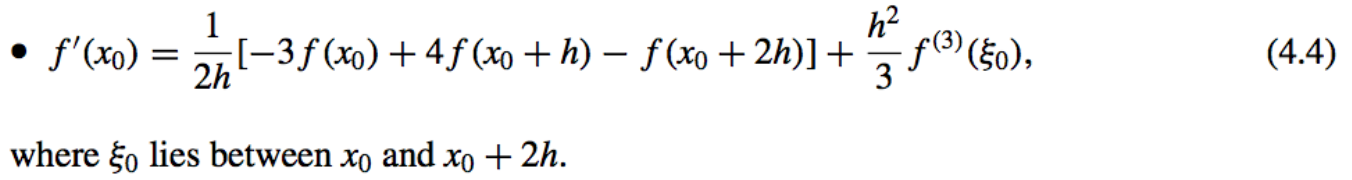
The approximation in Eq. (4.4) is useful near the ends of an interval, because information about f outside the interval may not be available.

Errors: the errors in both Eq. (4.4) and Eq. (4.5) are \(O(h^2)\)
Three-Point Midpoint Formula:

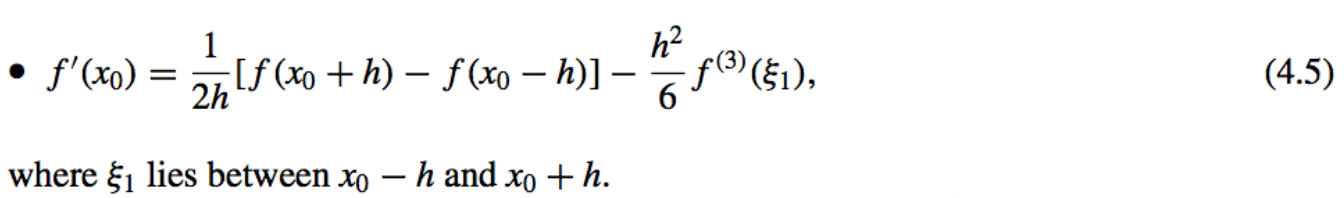
Errors: Although the errors in both Eq. (4.4) and Eq. (4.5) are \(O(h^2)\), the error in Eq. (4.5) is approximately half the error in Eq. (4.4).

This is because Eq. (4.5) uses data on both sides of \(x_0\) and Eq. (4.4) uses data
on only one side. Note also that f needs to be evaluated at only two points in Eq. (4.5), whereas in Eq. (4.4) three evaluations are needed.

What?
They are five-point formulas that involve evaluating the function at two additional points to the three-point formulas.
Why?
One common five-point formula is used to determine approximations for the derivative at the midpoint.
Error:
The error term for these formulas is \(O(h^4)\).
Five-Point Midpoint Formula:

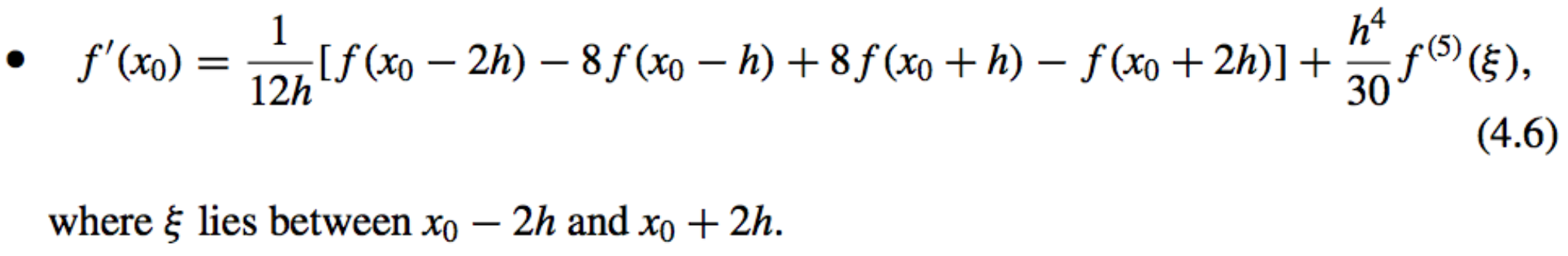
Used for approximation at Mid-Points
Five-Point Endpoint Formula:

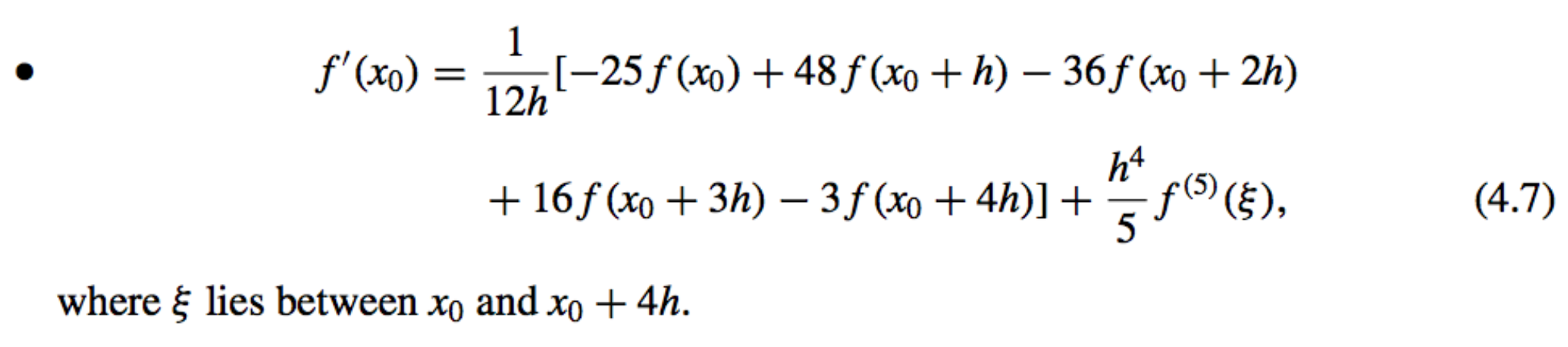
Used for approximation at End-Points

Left-endpoint approximations are found using this formula with \(h > 0\) and right-endpoint approximations with \(h < 0\).

The five-point endpoint formula is particularly useful for the clamped cubic spline interpolation of Section 3.5.

Approximations to Second Derivatives:

Derivation below
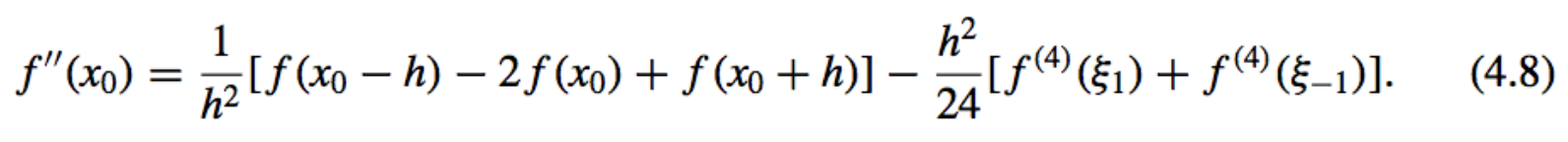
Second Derivative Midpoint Formula:

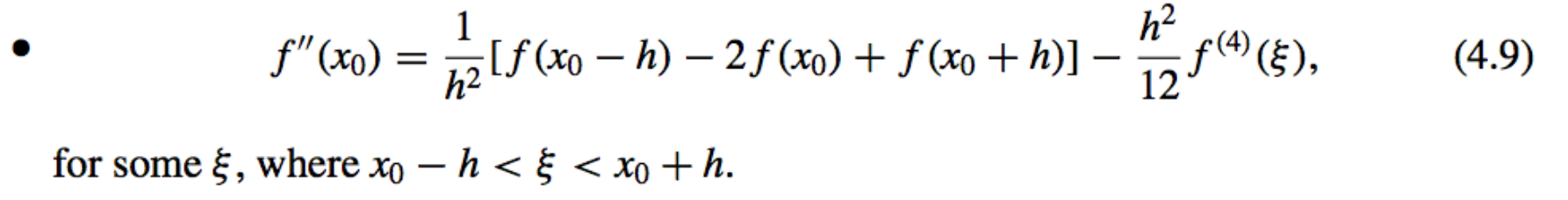
Error Bound: If \(f^{(4)}\) is continuous on \([x_0 − h, x_0 + h]\) it is also bounded, and the approximation is \(O(h^2)\).

Form of Error:
- We assume that our computations actually use the values \(\tilde{f}(x_0 + h)\) and \(\tilde{f}(x_0 − h)\)
- which are related to the true values \(f(x_0 + h)\) and \(f(x_0 − h)\) by:
  
  \(f(x_0 + h) = \tilde{f}(x_0 + h) + e(x_0 + h) \ \\) &
  \(f(x_0 − h) = \tilde{f}(x_0 − h) + e(x_0 − h)\)
The Total Error:

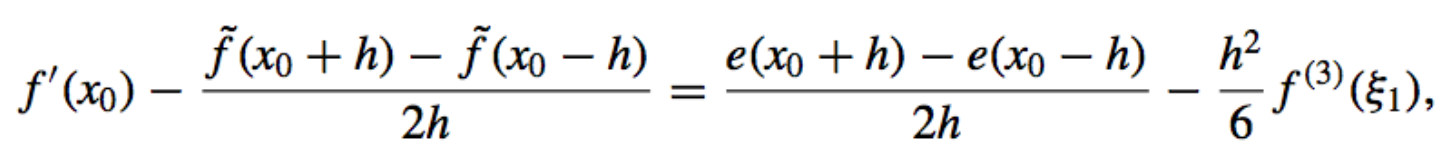
It is due both to round-off error, the first part, and to truncation error.
Error Bound:

If we assume that the round-off errors \(e(x_0 ± h)\) are bounded by some number \(ε > 0\)and that the third derivative of \(f\) is bounded by a number \(M > 0\), then
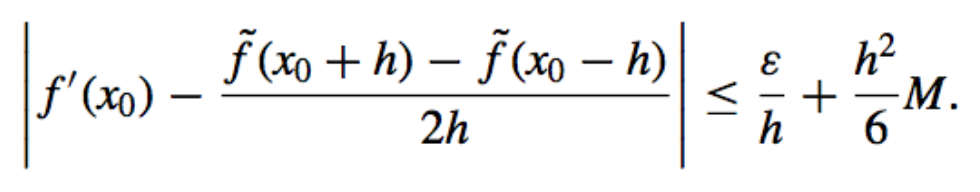
Reducing Truncation Error:
- How? To reduce the truncation error, \(\dfrac{h**2}{6}M\), we need to reduce \(h\).
- Effect of reducing \(h\): But as \(h\) is reduced, the roundoff error \(\dfrac{ε}{h}\) grows.
Conclusion:
- It is seldom advantageous to let \(h\) be too small, because in that case the round-off error will dominate the calculations.
- But we must remain aware that reducing the step size will not always improve the approximation.
- As approximation methods, numerical differentiation is unstable.