Extrapolation

1. What?
   
   • Extrapolation that is used to generate high-accuracy results while using low-order formulas.
   • Extrapolation can be applied whenever it is known that an approximation technique has an error term with a predictable form, one that depends on a parameter, usually the step size \(h\).
   • Suppose that for each number \(h \neq 0\) we have a formula \(N_1(h)\) that approximates an unknown constant \(M\), and that the truncation error involved with the approximation has the form,
     \(M − N_1(h) = K_1h + K_2h^2 + K_3h^3 +··· ,\)
     for some collection of (unknown) constants \(K_1, K_2, K_3, ...\) .
   • The truncation error is \(O(h)\), so unless there was a large variation in magnitude among the constants \(K_1, K_2, K_3, ... ,\)
     \(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ M − N_1(0.1) \approx 0.1K_1,\ \ \ \ \ \ \ \ M − N_1(0.01) \approx 0.01K_1,\)
     and, in general,
     \(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ M − N_1(h) \approx K_1h\) .
   • The object of extrapolation is to find an easy way to combine these rather inaccurate \(O(h)\) approximations in an appropriate way to produce formulas with a higher-order truncation error.
2. Why?
   
   • We can combine the \(N_1(h)\) formulas to produce an \(\mathcal{O}(h^2)\) approximation formula, \(N_2(h)\), for \(M\) with
     \(M − N_2(h) = \hat{K}_2h^2 + \hat{K}_3h^3 +···\) ,
     for some, again unknown, collection of constants \(\hat{K}_2, \hat{K}_3, ...\).
     Then we would have
     \(M − N_2(0.1) \approx 0.01\hat{K}_2, M − N_2(0.01) \approx 0.0001\hat{K}_2,\)
   • If the constants \(K_1\) and \(\hat{K}_2\) are roughly of the same magnitude, then the \(N_2(h)\) approximations would be much better than the corresponding \(N_1(h)\) approximations.
3. The \(\mathcal{O}(h)\) formula for approximating \(M\):
   

   The First Formula:
   

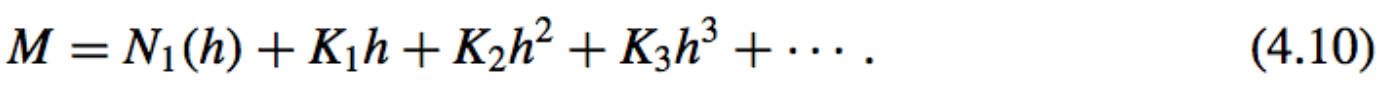
   The Second Formula:
   

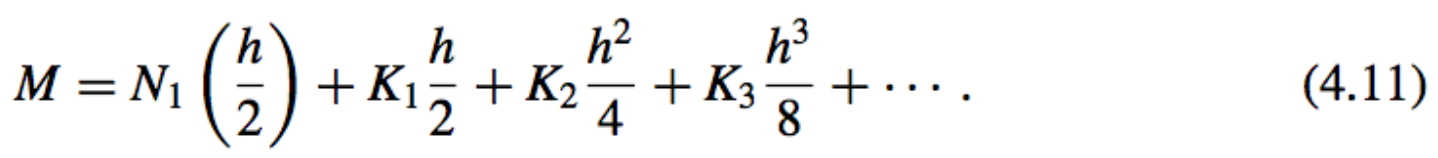
4. The \(\mathcal{O}(h^2)\) approximation formula for M:
   
   Show Derivation

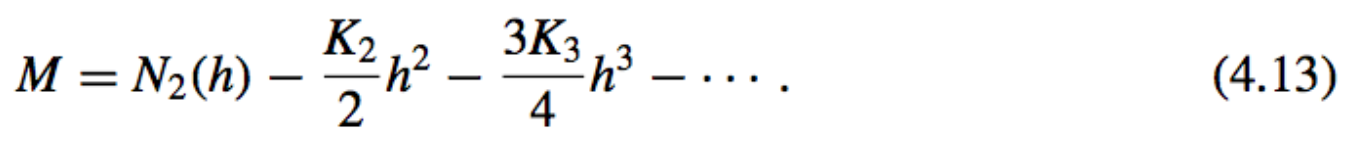
5. When to apply Extrapolation?
   

   Extrapolation can be applied whenever the truncation error for a formula has the form:
   

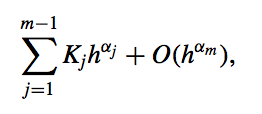
   for a collection of constants \(K_j\) and when \(\alpha_1 < \alpha_2 < \alpha_3 < ··· < \alpha_m\).

   The extrapolation is much more effective than when all powers of \(h\) are present because the averaging process produces results with errors \(\mathcal{O}(h^2), \mathcal{O}(h^4), \mathcal{O}(h^6), ...\), with essentially no increase in computation, over the results with errors, \(\mathcal{O}(h), \mathcal{O}(h^2), \mathcal{O}(h^3), ...\) .

6. The \(\mathcal{O}(h^4)\) formula for approximating \(M\):
   

   Derivation below

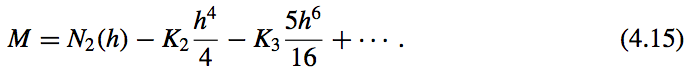
7. The \(\mathcal{O}(h^6)\) formula for approximating \(M\):
   

   Derivation below

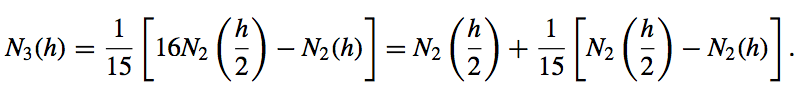
8. The \(\mathcal{O}(h^{2j})\) formula for approximating \(M\):
   
   Show Derivation

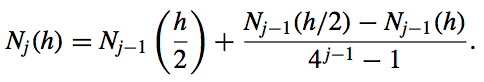
9. The Order the Approximations Generated:
   

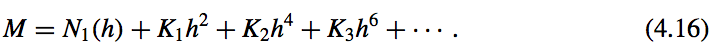
   It is conservatively assumed that the true result is accurate at least to within the agreement of the bottom two results in the diagonal, in this case, to within
   \(|N_3(h) − N_4(h)|\).

   

Deriving n-point Formulas with Extrapolation

1. Deriving Five-point Formula:
   Show Derivation