Table of Contents
Numerical Quadrature
-
- What?
- The basic method involved in approximating \(\int_{a}^{b} f(x) dx\).
-
- How?
- It uses a sum \(\sum_{i=0}^{n} a_i f(x_i)\) to approximate \(\int_{a}^{b} f(x) dx\).
-
- Based on:
- The methods of quadrature in this section are based on the interpolation polynomials given in Chapter 3.
- Method:
- Select a set of distinct nodes \({x_0, ... , x_n}\) from the interval \([a, b]\).
- Then integrate the Lagrange interpolating polynomial
\(P_n(x) = \sum_{i=0}^{n} f(x_i)L_i(x)\)
and its truncation error term over \([a, b]\) to obtain
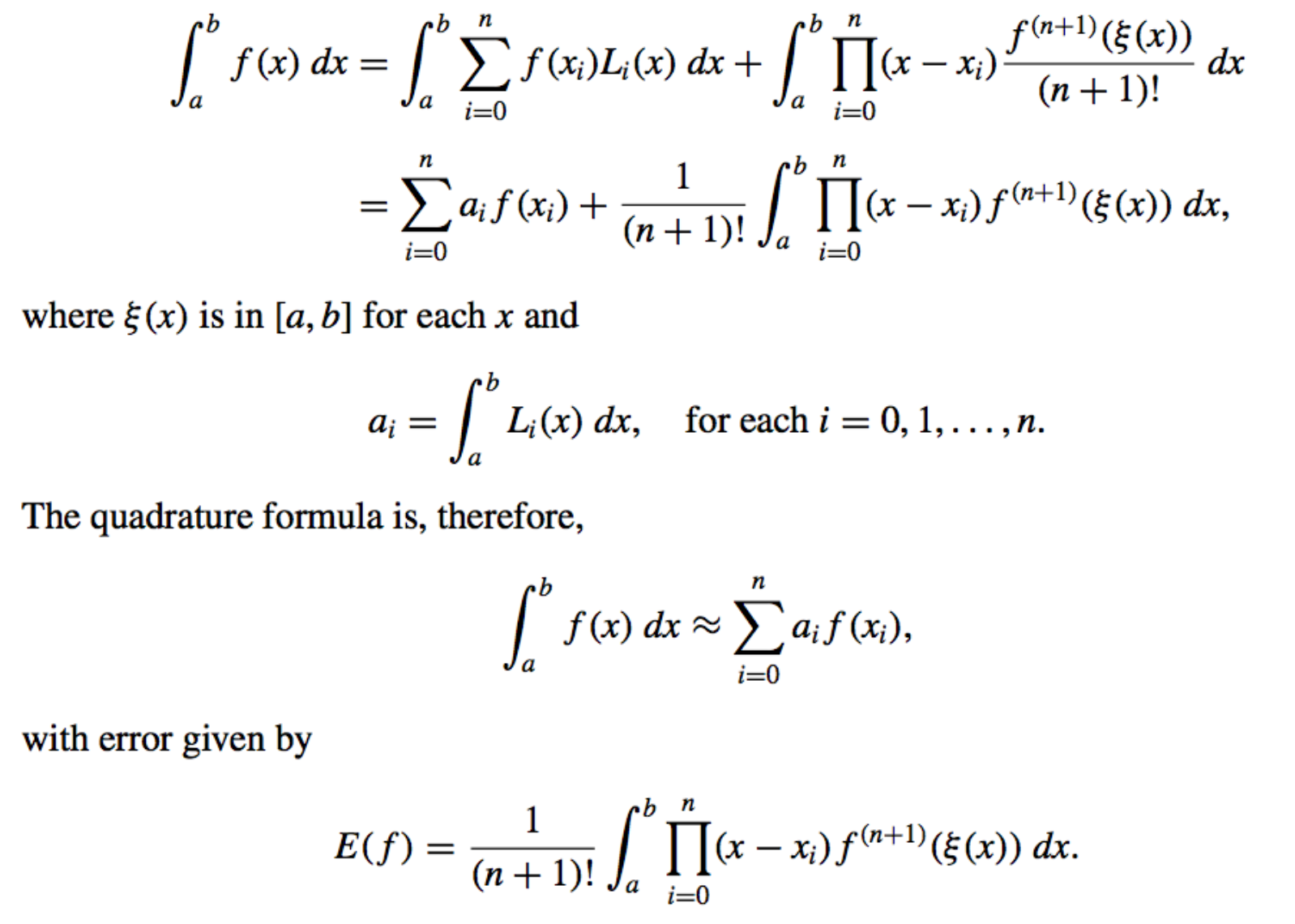
-
The Quadrature Formula:
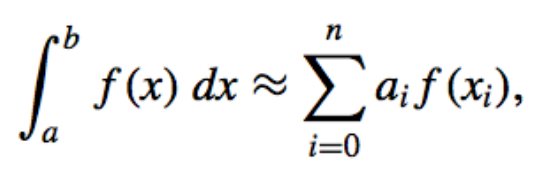
- The Error:
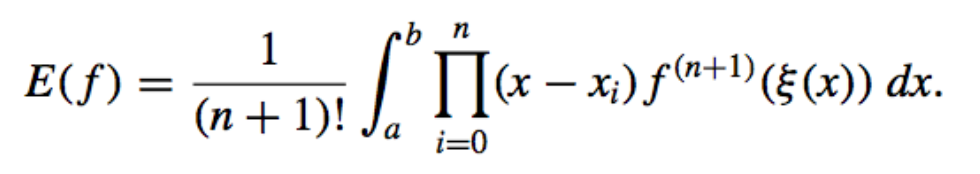
The Trapezoidal Rule
-
- What?
- Approximation method for integrals produced by using first (linear) Lagrange polynomials with equally-spaced nodes.
-
The Trapezoidal Rule:
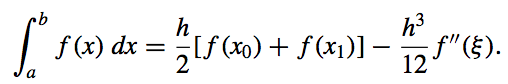

- Error:
The error term for the Trapezoidal rule involves \(f\) , so the rule gives the exact result when applied to any function whose second derivative is identically zero, that is, any polynomial of degree one or less.
Simpson’s Rule
- What?
A method to approximate an integral that results from integrating over \([a, b]\) the second Lagrange polynomial with equally-spaced nodes \(x_0 = a, x_2 = b,\) and \(x_1 = a + h\), where \(h = \dfrac{(b − a)}{2}\). - Simpson’s Rule:
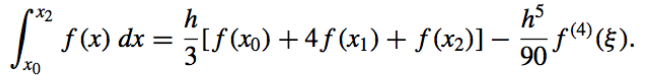

- Error:
The error term in Simpson’s rule involves the fourth derivative of \(f\) , so it gives exact results when applied to any polynomial of degree three or less.
Measuring Precision
- What?
The standard derivation of quadrature error formulas is based on determining the class of polynomials for which these formulas produce exact results. - Precision [degree of accuracy]:
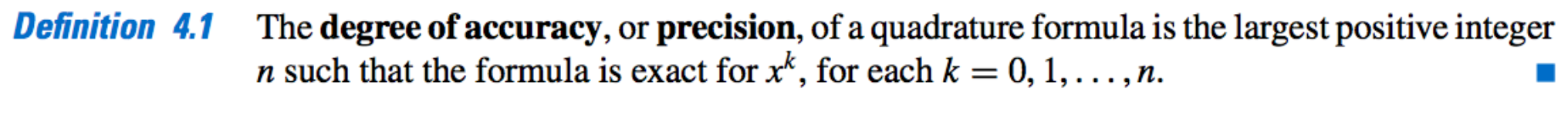
Definition 4.1 implies that the Trapezoidal and Simpson’s rules have degrees of precision one and three, respectively.
- Precision of Quadrature Formulas:
- The degree of precision of a quadrature formula is n if and only if the error is zero for all polynomials of degree \(k = 0, 1, ... , n\), but is not zero for some polynomial of degree \(n + 1\).
- The Trapezoidal and Simpson’s rules are examples of a class of methods known as Newton-Cotes formulas.
- Types of Newton-Cotes formulas: There are 2 types, Open, and Closed.
Closed Newton-Cotes Formulas
- What?
- The \((n+1)\)-point closed Newton-Cotes formula uses nodes \(x_i = x_0 +ih\), for \(i = 0, 1, ... , n,\) where \(x_0 = a, x_n = b\) and \(h = \dfrac{(b − a)}{n}\) .
- It is called closed because the endpoints of the closed interval [a, b] are included as nodes.
- Form of the Formula:
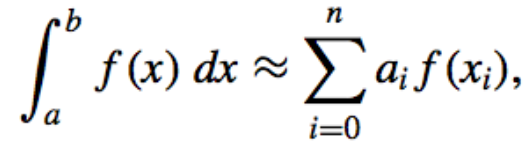
where,
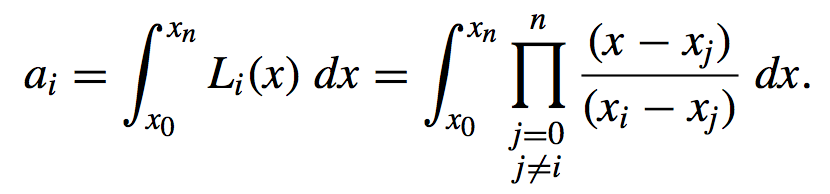
-
The Error Analysis:
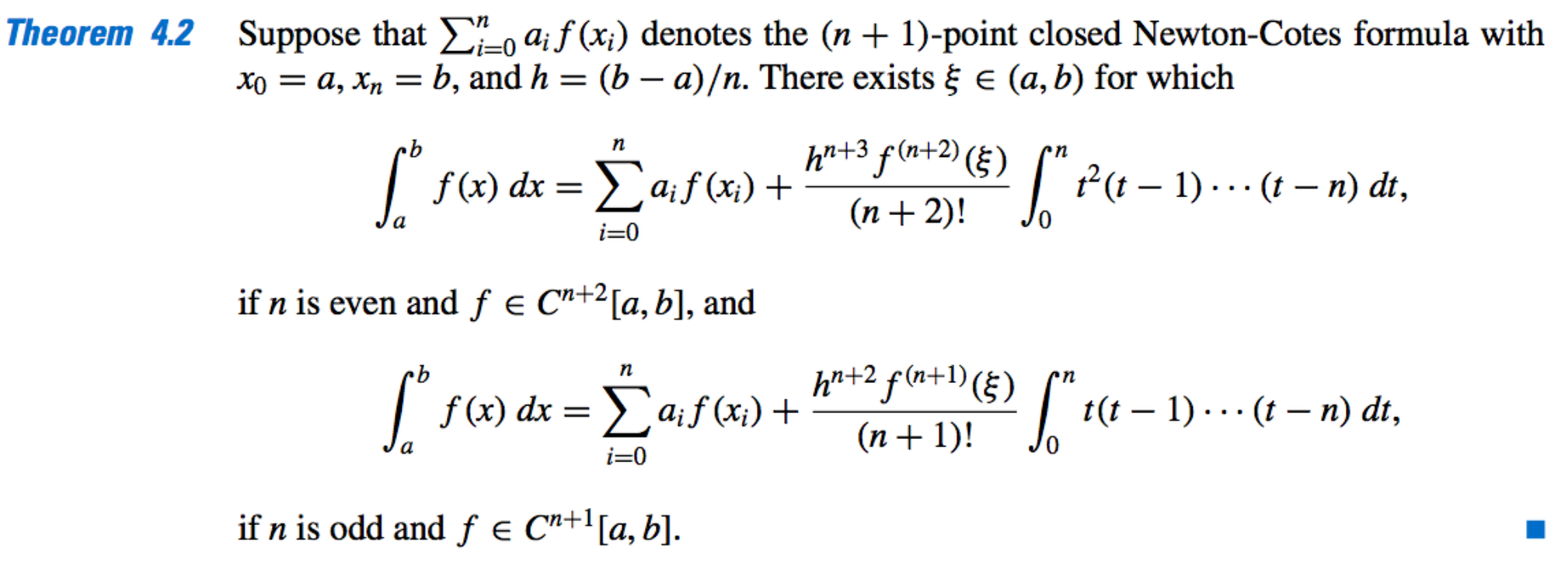
- Degree of Preceision:
- Even-n: the degree of precision is \(n + 1\) (although the interpolation polynomial is of degree at most n)
- Odd-n: the degree of precision is only \(n\).
- Closed Form Formulas:
- \(n = 1\): Trapezoidal rule
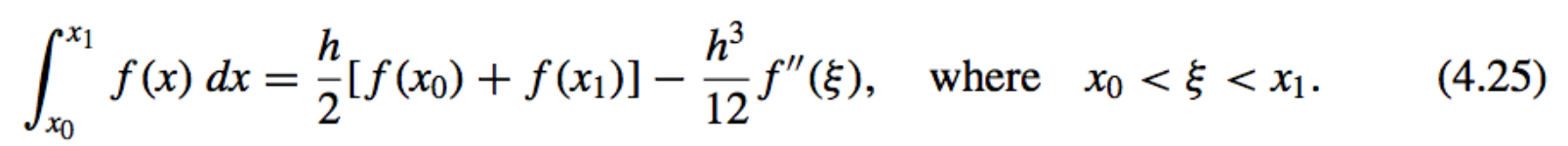
- \(n = 2\): Simpson’s rule
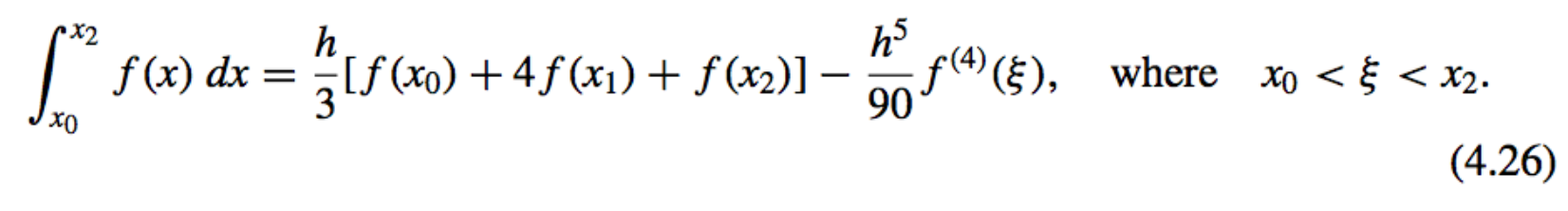
- \(n = 3\): Simpson’s Three-Eighths rule
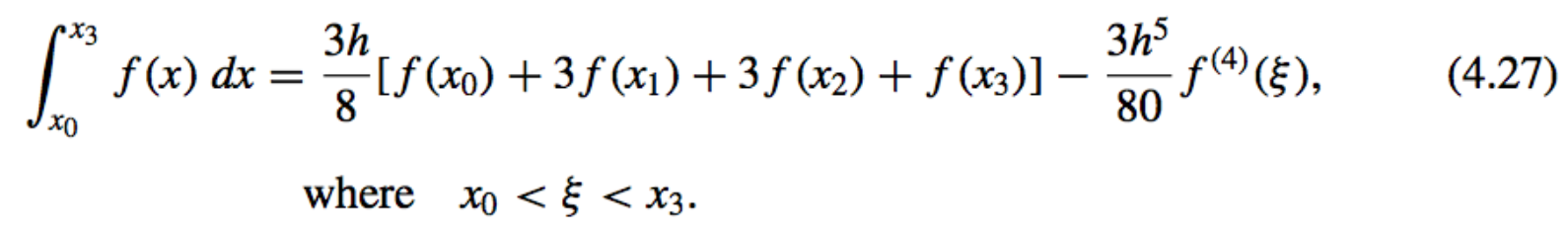
- n = 4:
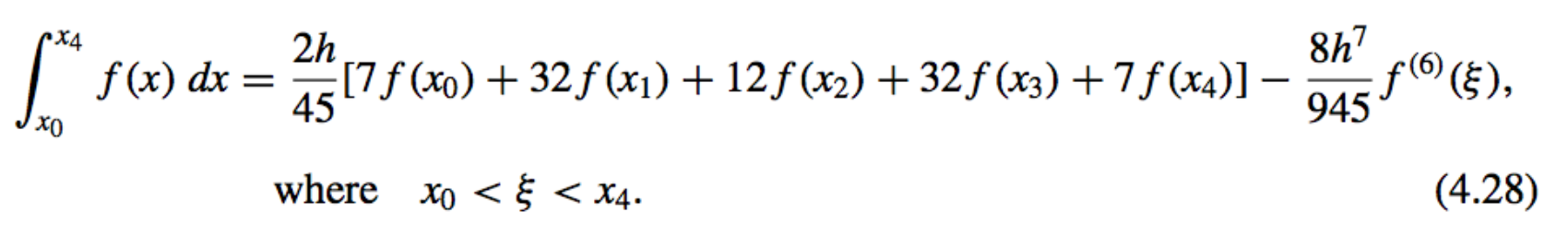
- \(n = 1\): Trapezoidal rule
Open Newton-Cotes Formulas
- What?
- They do not include the endpoints of \([a, b]\) as nodes.
- They use the nodes \(x_i = x_0 + ih\), for each \(i = 0, 1, ... , n\), where \(h = \dfrac{b − a}{n + 2}\) and \(x_0 = a + h\).
- This implies that \(x_n = b − h\), so we label the endpoints by setting \(x_{−1} = a\) and \(x_{n+1} = b\).
- Open formulas contain all the nodes used for the approximation within the open interval \((a, b)\)
- Form of the Formula:
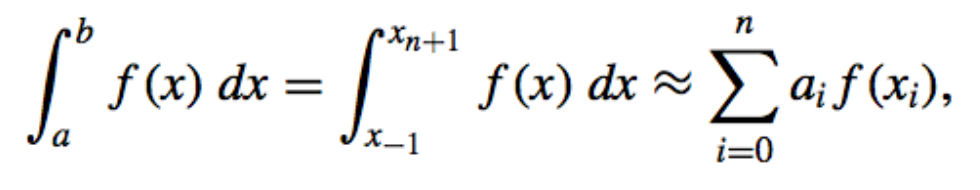
where,
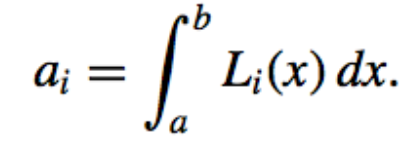
-
The Error Analysis:
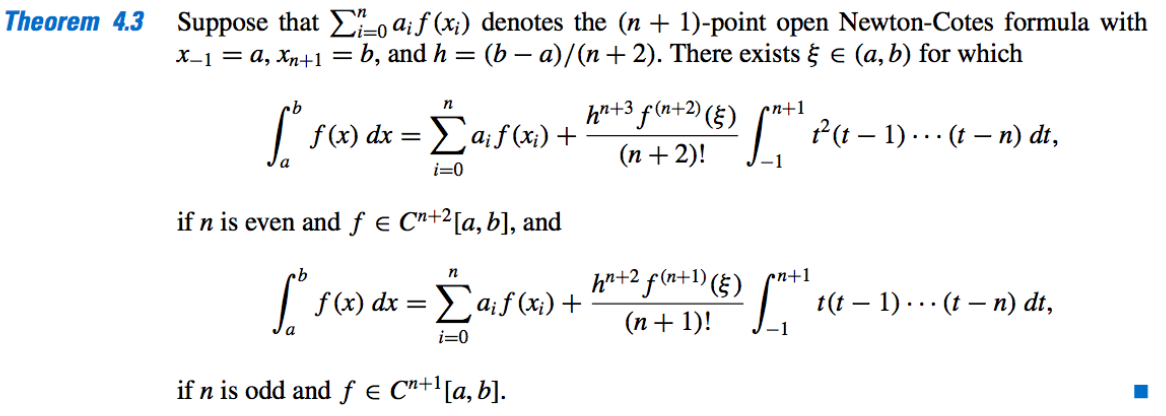
- Degree of Preceision:
- Even-n: Higher.
- Odd-n: Lower.
- Open Form Formulas:
- \(n = 0\): Midpoint rule
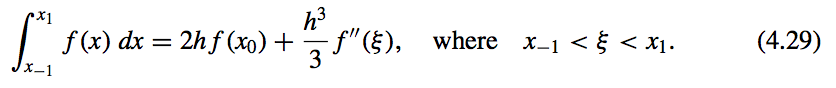
- \(n = 1\):
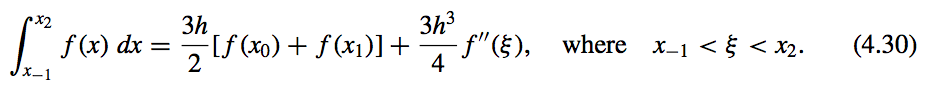
- \(n = 2\):
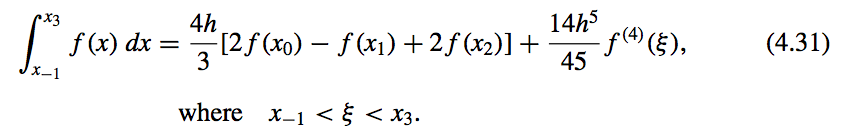
- n = 3:
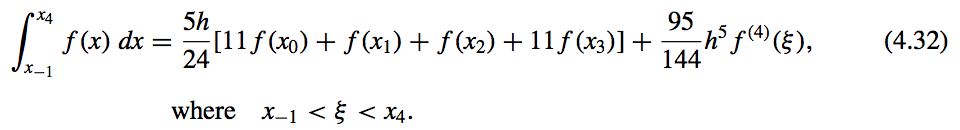
- \(n = 0\): Midpoint rule