Composite Rules

1. What?
   A piecewise approach to numerical integration that uses the low-order Newton-Cotes formulas.
2. Why?
   
   • The Newton-Cotes formulas are generally unsuitable for use over large integration intervals.
   • High-degree formulas would be required, and the values of the coefficients in these formulas are difficult to obtain.
   • Newton-Cotes formulas are based on interpolatory polynomials that use equally-spaced nodes, a procedure that is inaccurate over large intervals because of the oscillatory nature of high-degree polynomials.

3. Notice:

   \(h = \dfrac{b − a}{n}\) and \(x_j = a + jh\)

Composite Simpson’s rule

1. Composite Simpson’s rule:
   
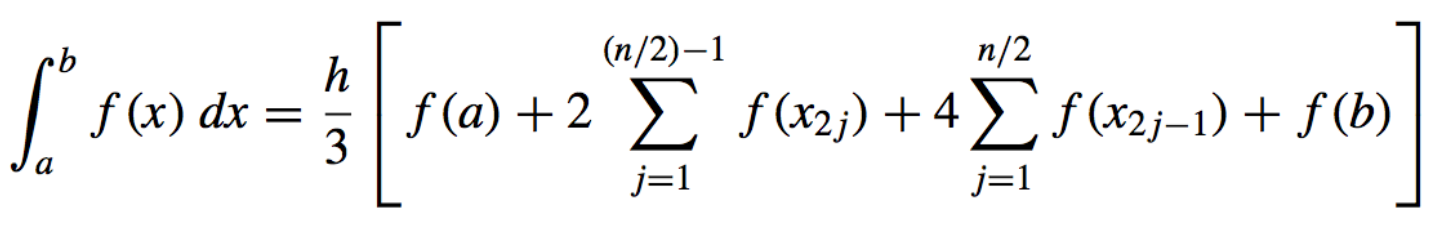
2. Error in Comoposite Simpson’s Rule:
   

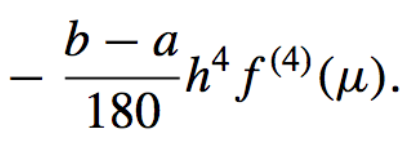
   Error \(\ \ \in \ \ \ \mathcal{O}(h^4)\)

3. Theorem [Rule and Error]:
   
4. Algorithm:
   

Composite Newton-Cotes Rules

1. Composite Trapezoidal rule:
   
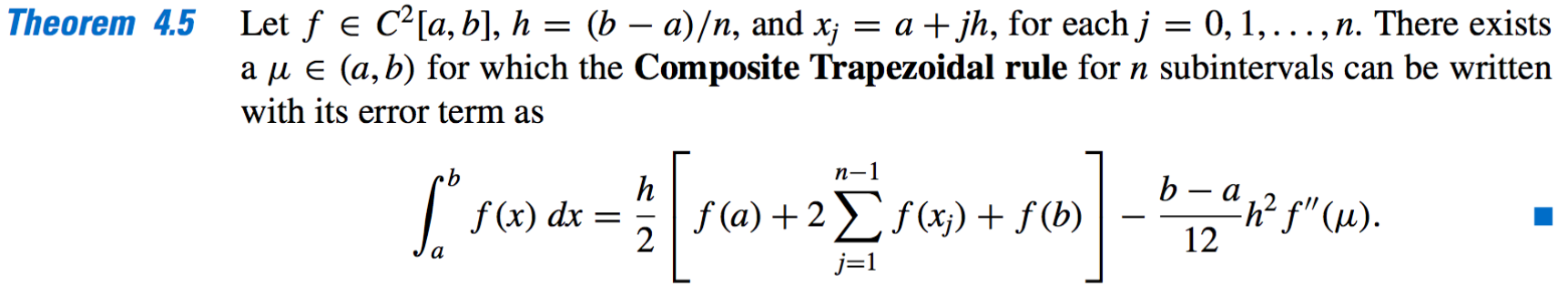
2. Composite Midpoint rule:
   

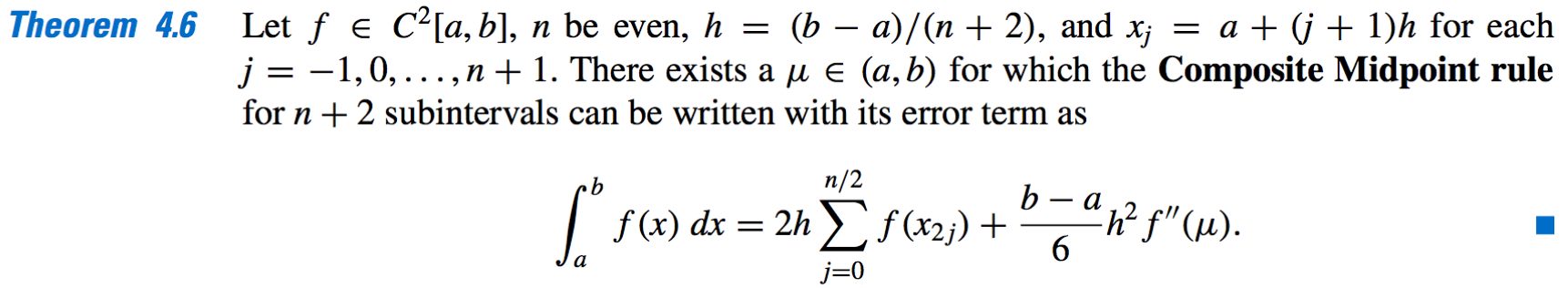
Round-Off Error Stability

1. Stability Property:
   An important property shared by all the composite integration techniques is a stability with respect to round-off error.
   The round-off error does not depend on the number of calculations performed.
2. Proof:
   Show Derivation