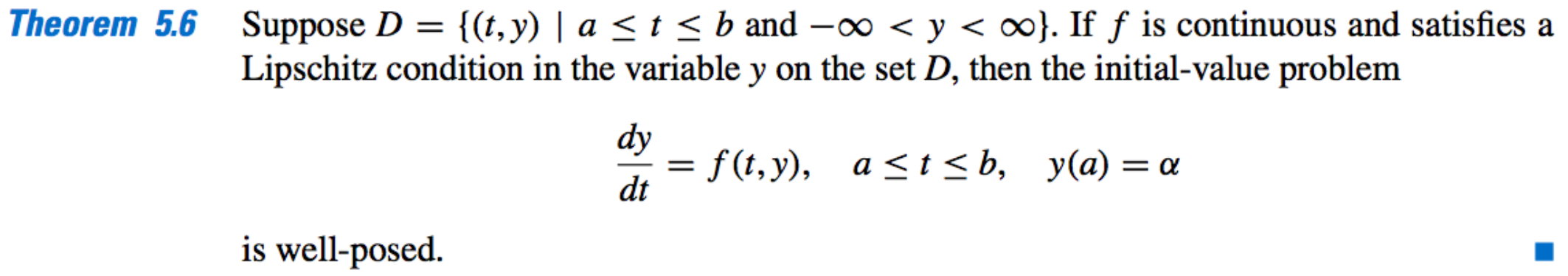Theory of IVP

1. Lipschitz Condition:
   

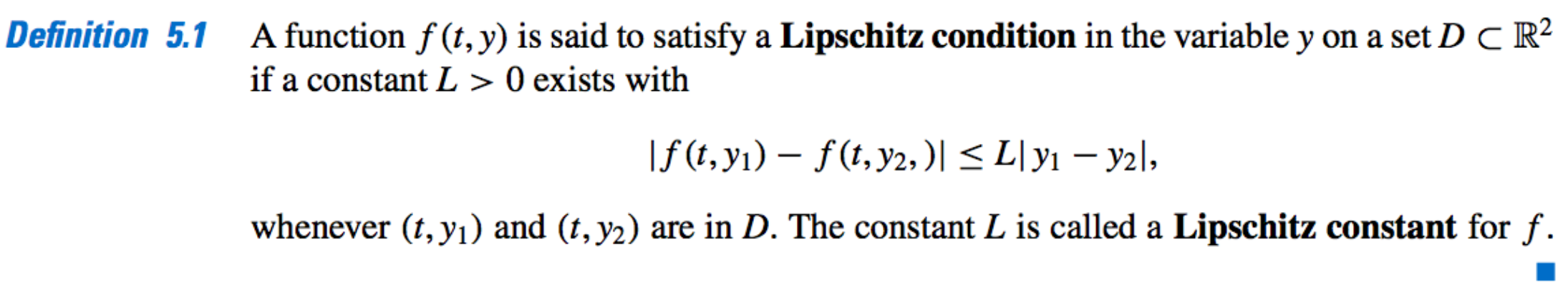
2. Convex Set:
   

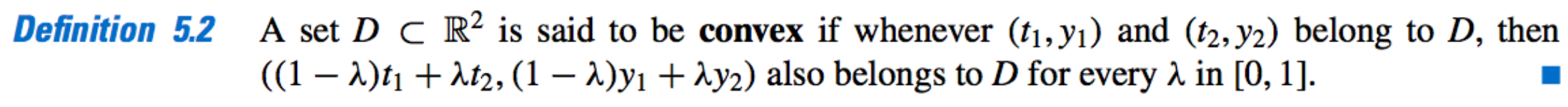
3. Lipschitz Condition on Convex Sets:
   

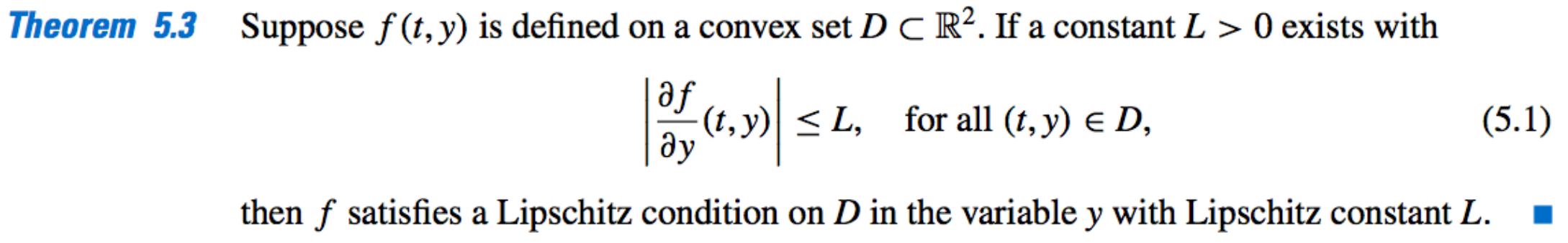
4. Existence and Uniqueness Theorem for First-Order ODEs:
   

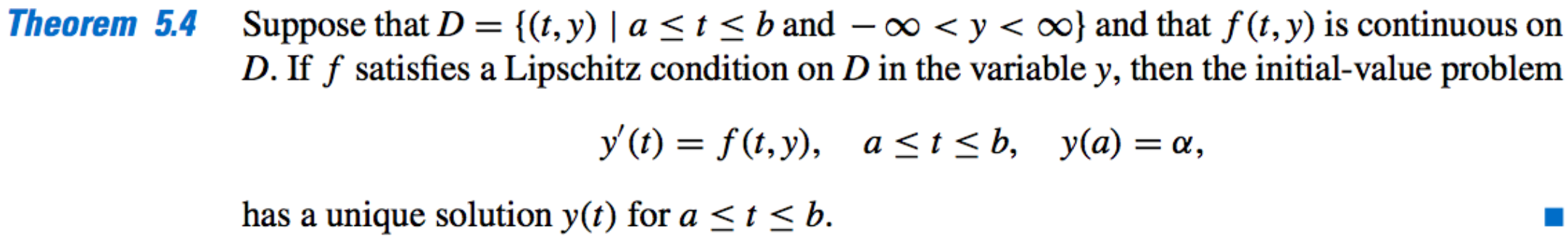
Well-Posed Problems

1. What?

   It is the property that small changes, or perturbations, in the statement of the problem introduce correspondingly small changes in the solution.

2. Why?

   Due to round-off errors and measurment error we need to make sure the result of such small errors is minuscule.

3. A Well-Posed Problem:
   

   The problem specified by (5.3) is called a perturbed problem associated with the original problem (5.2).

   It assumes the possibility of an error being introduced in the statement of the differential equation, as well as an error δ0 being present in the initial condition.

4. Conditions for being Well-Posed: