Local Truncation Error

1. What?

   The local truncation error at a specified step measures the amount by which the exact solution to the differential equation fails to satisfy the difference equation being used for the approximation at that step.

2. Why?
   

   We need a means for comparing the efficiency of various approximation methods.

   The local truncation will serve quite well to determine not only the local error of a method but the actual approximation error.

3. Definition:
   

4. Why local?
   

   This error is a local error because it measures the accuracy of the method at a specific step, assuming that the method was exact at the previous step.

5. What does it depend on?
   

   As such, it depends on the differential equation, the step size, and the particular step in the approximation.

6. Euler Method Truncation Error:
   (5.7)

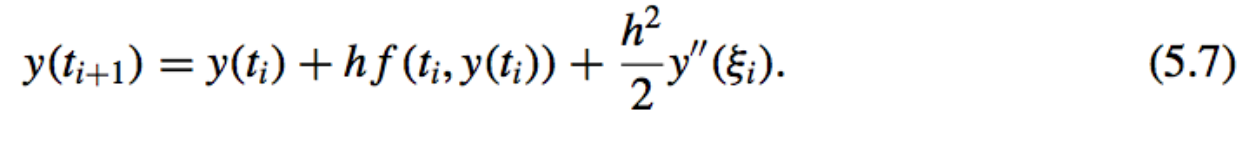
7. How to select difference equations methods?
   One way to select difference-equation methods for solving ordinary differential equations is in such a manner that their local truncation errors are O(hp) for as large a value of p as possible, while keeping the number and complexity of calculations of the methods within a reasonable bound.

Talors Method

1. Taylors Method of order n:
   Show Derivation

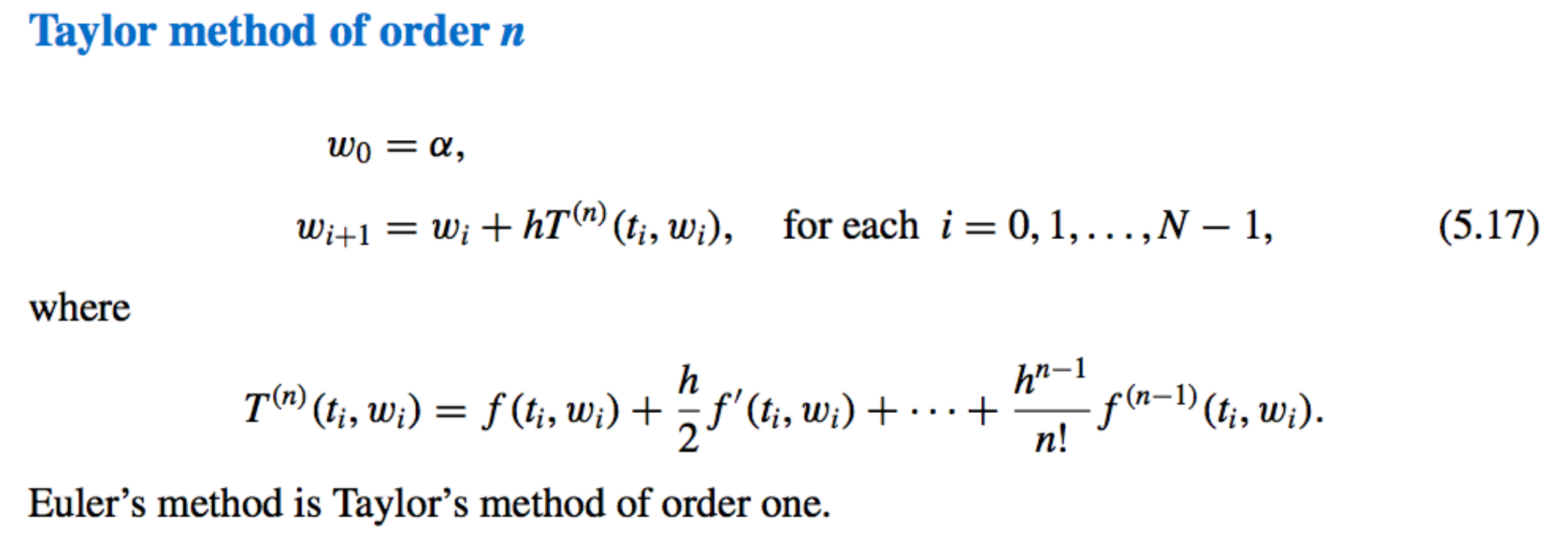
2. Approximation Theorem:
   Show Derivation

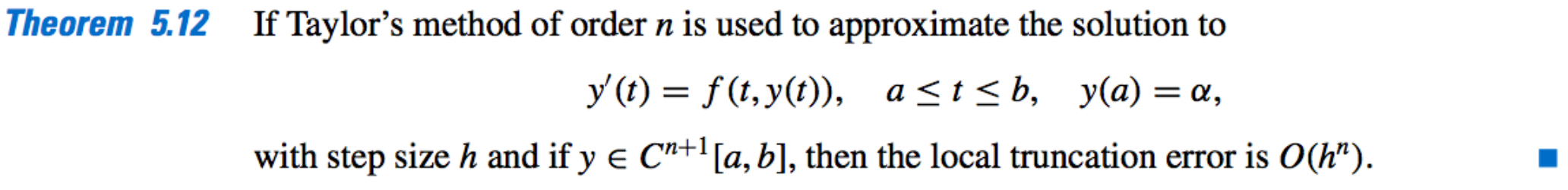
3. Using Hermite Polynomials to evaluate a differential equations at a midpoint:
   Show Example