Runge-Kutta methods

1. What?

2. Why?

   The Taylor methods outlined in the previous section have the desirable property of highorder local truncation error, but the disadvantage of requiring the computation and evaluation of the derivatives of \(f(t, y)\). This is a complicated and time-consuming procedure for most problems, so the Taylor methods are seldom used in practice.

   The Runge-Kutta methods have the high-order local truncation error of the Taylor methods but eliminate the need to compute and evaluate the derivatives of \(f(t, y)\)

3. Taylor’s Theorem [2-variables]:
   

Runge-Kutta Methods of Order Two

1. What? \

2. Midpoint Method:
   
   • 2nd order:
     
   • Higher order:
     

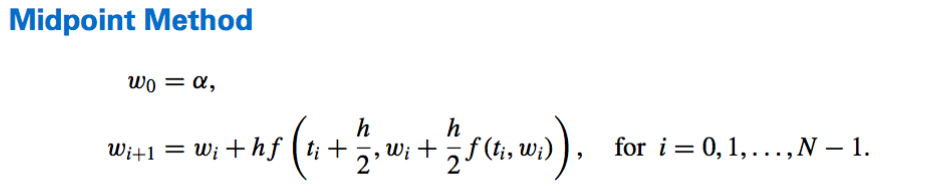
     The fact that (5.21) has four parameters, however, gives a flexibility in their choice, so a number of \(O(h^2)\) methods can be derived.
     Show Derivation

3. Modified Euler Method:
   

   One of the most important is the Modified Euler method, which corresponds to choosing \(a_1 = a_2 = \dfrac{1}{2}\) and \(\alpha_2 = \delta_2 = h\). It has the following difference-equation form:
   

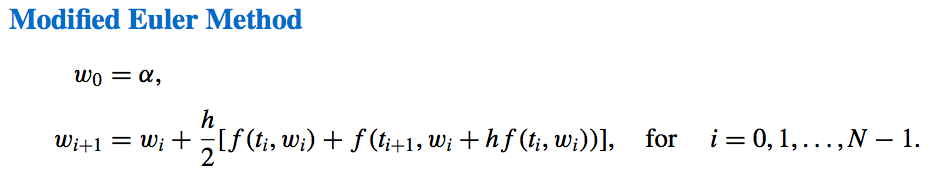
4. Error Order:
   

   The order of error for this new method is the same as that of the Taylor method of order two.

Higher-Order Runge-Kutta Methods

1. What? The term \(T^{(3)}(t, y)\) can be approximated with error \(O(h^3)\) by an expression of the form \(f(t + \alpha_1, y + \delta_1 f(t + \alpha_2, y + \delta_2 f(t, y)))\), involving four parameters, the algebra involved in the determination of \(\alpha_1, \delta_1, \alpha_2,\) and \(\delta_2\) is quite involved.

2. Heun’s method:
   

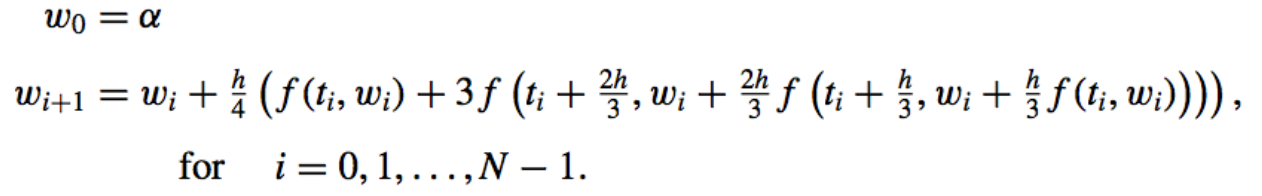
   • Local Truncation Error: \(\mathcal{O}(h^3)\).
3. Runge-Kutta Order Four:
   
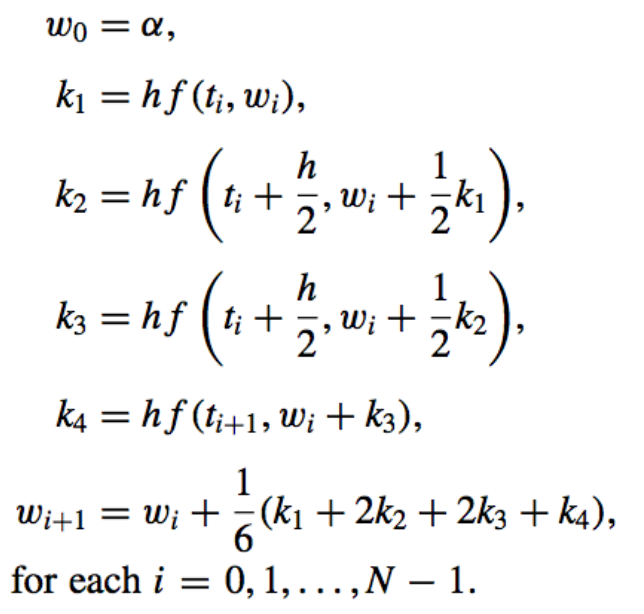
   • Local Truncation Error: \(\mathcal{O}(h^4)\).

     Provided the solution \(y(t)\) has five continuous derivatives.

   • Algorithm:
     Show Algorithm

Computational Comparisons

1. What is Compuatation Heavy?

   The main computational effort in applying the Runge-Kutta methods is the evaluation of \(f\).

2. Function Evaluations:
   

   • Second Order:

     2 function evaluations per step

     Error of order \(\mathcal{O}(h^2)\).

   • Fourth Order:

     4 function evaluations per step

     Error of order \(\mathcal{O}(h^4)\).

3. Relationship between number of evaluations and order of truncation error:
   

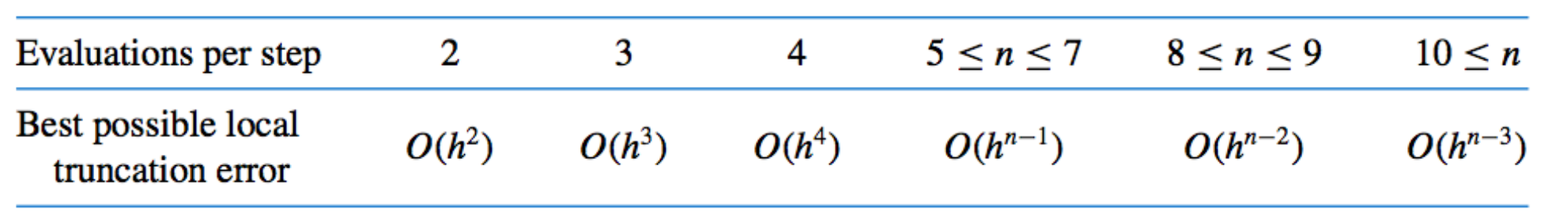
   This indicates why the methods of order less than five with smaller step size are used in preference to the higher-order methods using a larger step size.

   This is because..

4. Comparing lower-order Runge-Kutta Methods:
   The Runge-Kutta method of order four requires four evaluations per step, whereas Euler’s method requires only one evaluation. Hence if the Runge-Kutta method of order four is to be superior it should give more accurate answers than Euler’s method with one-fourth the step size. Similarly, if the Runge-Kutta method of order four is to be superior to the second-order Runge-Kutta methods, which require two evaluations per step, it should give more accuracy with step size h than a second-order method with step size h/2.

   This indeed holds true.