Table of Contents

Adaptive Methods

  1. What?

    Techniques used to control the error of a difference equation method in an efficient manner by the appropriate choice of mesh points.

    By using methods of differing order we can predict the local truncation error and, using this prediction, choose a step size that will keep it and the global error in check.

  2. Why?
    Adaptive Methods incorporate in the step-size procedure an estimate of the truncation error that does not require the approximation of the higher derivatives of the function.
    They adapt the number and position of the nodes used in the approximation to ensure that the truncation error is kept within a specified bound.
  3. Derivation:

Runge-Kutta-Fehlberg Method

  1. What?
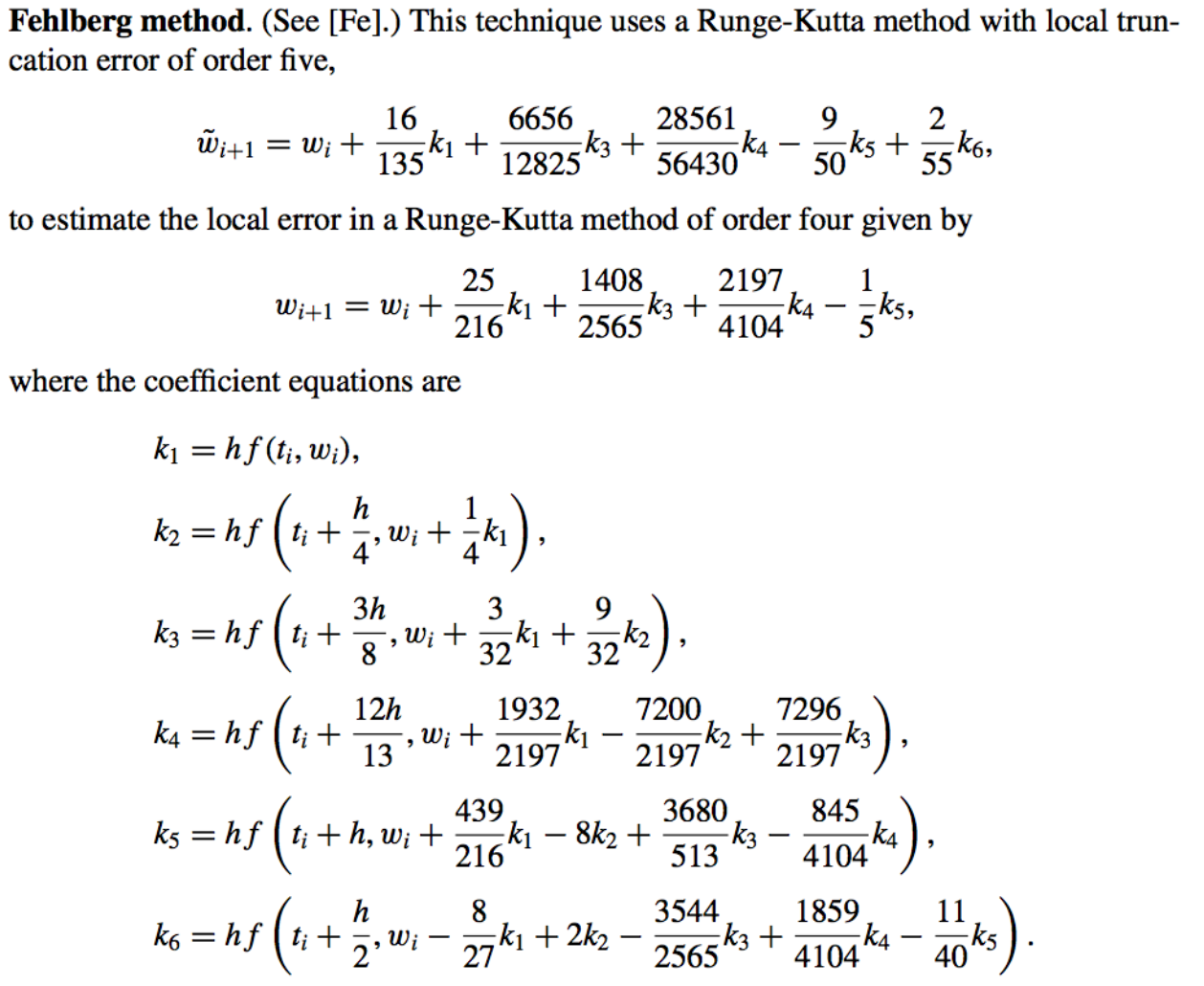
    formula

  2. Why?

    An advantage to this method is that only six evaluations of f are required per step.

    As opposed to requiring at least four evaluations of \(f\) for the fourth-order method and an additional six for the fifth-order method, for a total of at least ten function evaluations.

    \(\implies\) This Method has at least a \(40\%\) decrease in the number of function evaluations over the use of a pair of arbitrary fourth- and fifth-order methods.

  3. Error Bound Order:
    \(\mathcal{O}(h^5)\)

  4. The choice of “q”:
    • The value of q determined at the ith step is used for two purposes:
      1. When \(q < 1\): to reject the initial choice of \(h\) at the ith step and repeat the calculations using \(qh\), and
      2. **When \(q \geq 1\): to accept the computed value at the ith step using the step size \(h\), but change the step size to \(qh\) for the (i + 1)st step.

    Because of the penalty in terms of function evaluations that must be paid if the steps are repeated, q tends to be chosen conservatively.

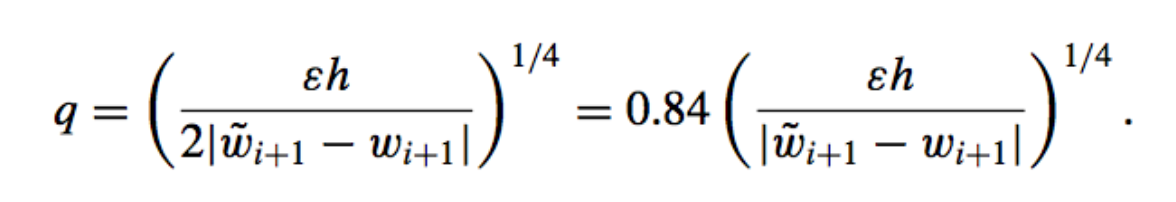
    • The choice of q for the “Runge-Kutta-Fehlberg”: formula
  5. Algorithm:
    • Notice:
      1. Step 9 is added to eliminate large modifications in step size.
      2. This is done to avoid spending too much time with small step sizes in regions with irregularities in the derivatives of y, and to avoid large step sizes, which can result in skipping sensitive regions between the steps.
      3. The step-size increase procedure could be omitted completely from the algorithm.
      4. The step-size decrease procedure used only when needed to bring the error under control.