Multi-Step Methods

1. What?

   Methods that use the information produced at the steps \(t_0, t_1, .. , t_{i-1}, t_i\), to approximate \(t_{i+1}\).

2. Why?

   Since the error \([\mid w_j − y(t_j) \mid]\) increases with each step, we know that the previously computed values of \(t\) are actually more accurate than those coming up next.

   Thus, it makes sense to use these more accurate values to produce the next result.

3. m-step Multistep Method:
   

4. Types of Methods:
   

   1. Open / Explicit Methods: If \(b_m = 0\) because Eq. \((5.24)\) then gives \(w_{i+1}\) explicitly in terms of previously determined values.

   2. Closed / Implicit Methods: If \(b_m \neq 0\) because \(w_{i+1}\) occurs on both sides of Eq. \((5.24)\), so \(w_{i+1}\) is specified, only, implicitly.

5. Open vs Closed / Explicit vs Implicit:
   In general, the coefficients of the terms involving \(f\) in the local truncation error are smaller for the implicit methods than for the explicit methods.

6. Starting Values:

   The starting values must be specified, generally by assuming \(w_0 = \alpha\) and generating the remaining values by either a Runge-Kutta or Taylor method.

7. Deriving Multi-Step Methods:
   

   Show Derivation

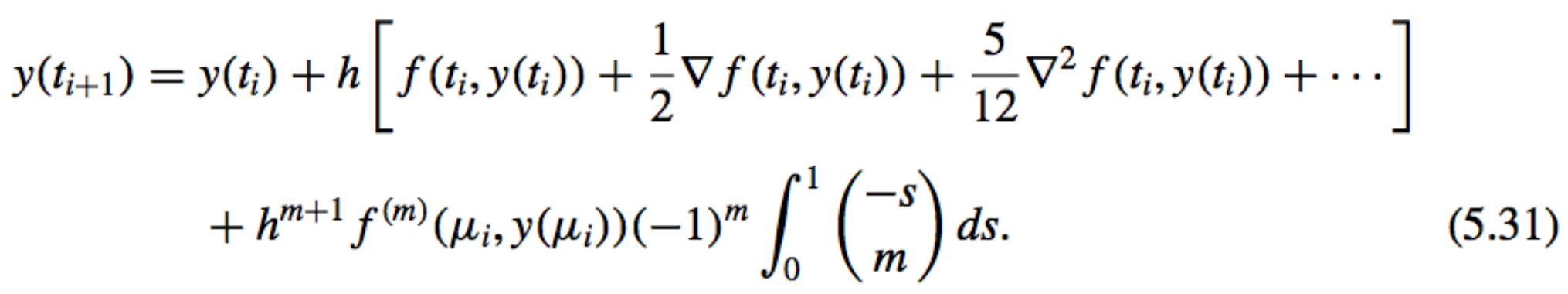
8. Example [Deriving three-step Adams-Bashforth]:
   Show Derivation

Adams-Bashforth Explicit Methods

1. Adams-Bashforth Two-Step Explicit Method:
   

2. Adams-Bashforth Three-Step Explicit Method:
   

3. Adams-Bashforth Four-Step Explicit Method:
   

4. Adams-Bashforth Five-Step Explicit Method:
   

Adams-Moulton Implicit Methods

1. What?

   Implicit methods are derived by using \((t_{i+1}, f(t_{i+1}, y(t_{i+1})))\) as an additional interpolation node in the approximation of the integral,

   \(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\) \(\ \ \ \ \ \ \ \\) \(\int_{t_{i+1}}^{t_i} f(t, y(t)) dt\).

2. Adams-Moulton Two-Step Implicit Method:
   

3. Adams-Moulton Three-Step Implicit Method:
   

4. Adams-Moulton Four-Step Implicit Method:
   

5. DrawBacks:
   To apply an implicit method, we must solve the implicit equation for \(w_{i+1}\).
   This is not always possible, and even when it can be done the solution for \(w_{i+1}\) may not be unique.

Predictor-Corrector Methods

1. What?

   The combination of an explicit method to predict and an implicit to improve the prediction.

2. Why?

   Even though the implicit methods are better than the explicit methods, they have the inherent weakness of first having to convert the method algebraically to an explicit representation for \(w_{i+1}\).

   This procedure is not always possible,
   WHY?

3. Derivation:
   Show Derivation

4. Algorithm:
   Show Algorithm

5. Milne’s method:
   

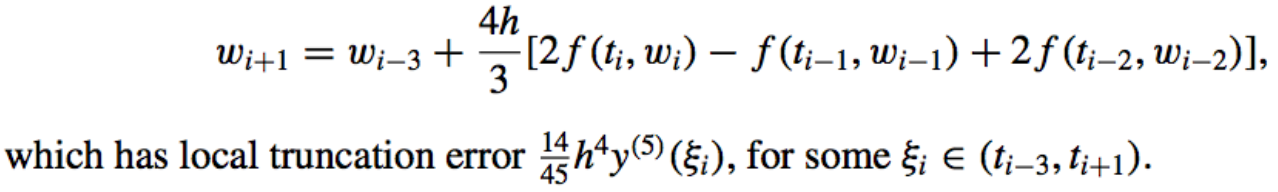
   Derived by integrating an interpolating polynomial over \([t_{i−3}, t_{i+1}]\).

6. Implicit Simpson’s Method:
   

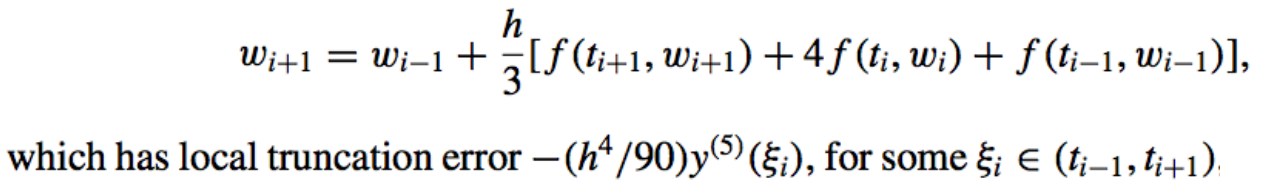
   Derived by integrating an interpolating polynomial over \([t_{i−1}, t_{i+1}]\).

7. Another Predictor-Corrector Method:
   

   • Milne’s method is occasionally used as a predictor for the implicit Simpson’s method.

   • Properties:

     1. The local truncation error involved with a predictor-corrector method of the Milne-Simpson type is generally smaller than that of the Adams-Bashforth-Moulton method.
     2. However, the technique has limited use because of round-off error problems, which do not occur with the Adams procedure.