Introduction and Architecture

1. From PCA to Auto-Encoders:
   - High dimensional data can often be represented using a much lower dimensional code.
   - This happens when the data lies near a linear manifold in the high dimensional space.
   - Thus, if we can find this linear manifold, we can project the data on the manifold and, then, represent the data by its position on the manifold without losing much information because in the directions orthogonal to the manifold there isn’t much variation in the data.

   Finding/Learning the Manifold:
   Often, PCA is used as a method to determine this linear manifold to reduce the dimensionality of the data from \(N\)-dimensions to, say, \(M\)-dimensions, where \(M < N\).
   - However, what if the manifold that the data is close to, is non-linear?
   Obviously, we need someway to find this non-linear manifold.

   Deep-Learning provides us with Deep AutoEncoders.
   Auto-Encoders allows us to deal with curved manifolds in the input space by using deep layers, where the code is a non-linear function of the input, and the reconstruction of the data from the code is, also, a non-linear function of the code.

   Using Backpropagation to implement PCA (inefficiently):
   Procedure

   - The reason to use backprop to implement PCA is that it allows us to generalize PCA.
   - With non-linear layers before and after the code, it should be possible to efficiently represent data that lies on or near a non-linear manifold.
   
   

2. Auto-Encoders:
   An AutoEncoder is an artificial neural network used for unsupervised learning of efficient codings.
   It aims to learn a representation (encoding) for a set of data, typically for the purpose of dimensionality reduction.
   

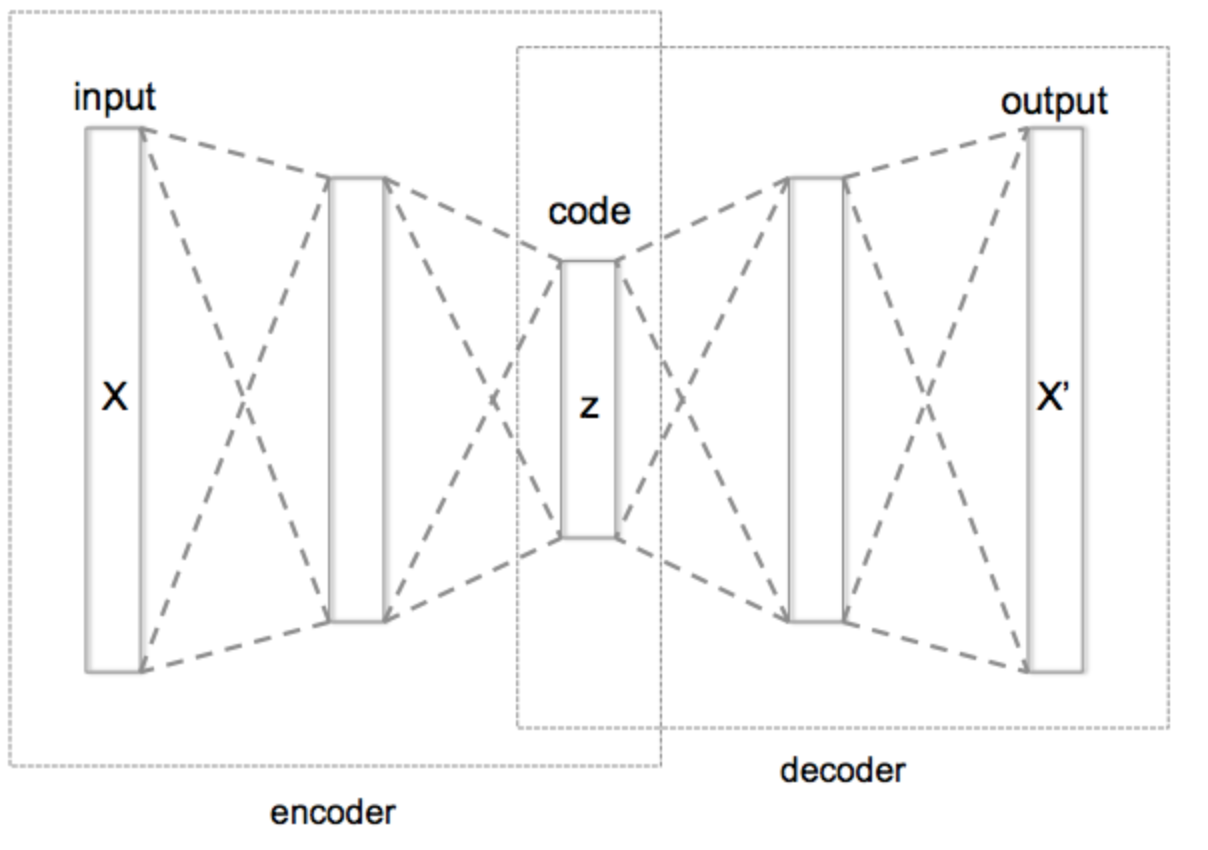
3. Deep Auto-Encoders:
   They provide a really nice way to do non-linear dimensionality reduction:
   • They provide flexible mappings both ways
   • The learning time is linear (or better) in the number of training examples
   • The final encoding model/Encoder is fairly compact and fast
     
     
4. Advantages of Depth:
   Autoencoders are often trained with only a single layer encoder and a single layer decoder, but using deep encoders and decoders offers many advantages:
   • Depth can exponentially reduce the computational cost of representing some functions
   • Depth can exponentially decrease the amount of training data needed to learn some functions
   • Experimentally, deep Autoencoders yield better compression compared to shallow or linear Autoencoders
     
     
5. Learning Deep Autoencoders:
   Training Deep Autoencoders is very challenging:
   • It is difficult to optimize deep Autoencoders using backpropagation
   • With small initial weights the backpropagated gradient dies

   There are two main methods for training:

   • Just initialize the weights carefully as in Echo-State Nets. (No longer used)
   • Use unsupervised layer-by-layer pre-training. (Hinton)
     This method involves treating each neighbouring set of two layers as a restricted Boltzmann machine so that the pretraining approximates a good solution, then using a backpropagation technique to fine-tune the results. This model takes the name of deep belief network.
   • Joint Training (most common)
     This method involves training the whole architecture together with a single global reconstruction objective to optimize.

   A study published in 2015 empirically showed that the joint training method not only learns better data models, but also learned more representative features for classification as compared to the layerwise method.
   The success of joint training, however, is mostly attributed (depends heavily) on the regularization strategies adopted in the modern variants of the model.

   Is Joint Training Better for Deep Auto-Encoders? (paper)
   

6. Architecture:
   An auto-encoder consists of:
   • An Encoding Function
   • A Decoding Function
   • A Distance Function

   We choose the encoder and decoder to be parametric functions (typically neural networks), and to be differentiable with respect to the distance function, so the parameters of the encoding/decoding functions can be optimized to minimize the reconstruction loss, using Stochastic Gradient Descent.

   The simplest form of an Autoencoder is a feedforward neural network (similar to the multilayer perceptron (MLP)) – having an input layer, an output layer and one or more hidden layers connecting them – but with the output layer having the same number of nodes as the input layer, and with the purpose of reconstructing its own inputs (instead of predicting the target value \({\displaystyle Y}\) given inputs \({\displaystyle X}\)).

7. Structure and Mathematics:
   The encoder and the decoder in an auto-encoder can be defined as transitions \(\phi\) and \({\displaystyle \psi ,}\) such that:

   $$ {\displaystyle \phi :{\mathcal {X}}\rightarrow {\mathcal {F}}} \\ {\displaystyle \psi :{\mathcal {F}}\rightarrow {\mathcal {X}}} \\ {\displaystyle \phi ,\psi =\arg \min_{\phi ,\psi }\|X-(\psi \circ \phi )X\|^{2}}$$

   where \({\mathcal {X} = \mathbf{R}^d}\) is the input space, and \({\mathcal {F} = \mathbf{R}^p}\) is the latent (feature) space, and \(p < d\).

   The encoder takes the input \({\displaystyle \mathbf {x} \in \mathbb {R} ^{d}={\mathcal {X}}}\) and maps it to \({\displaystyle \mathbf {z} \in \mathbb {R} ^{p}={\mathcal {F}}}\):

   $${\displaystyle \mathbf {z} =\sigma (\mathbf {Wx} +\mathbf {b} )}$$

   • The image \(\mathbf{z}\) is referred to as code, latent variables, or latent representation.
   • \({\displaystyle \sigma }\) is an element-wise activation function such as a sigmoid function or a rectified linear unit.
   • \({\displaystyle \mathbf {W} }\) is a weight matrix
   • \({\displaystyle \mathbf {b} }\) is the bias.

   The Decoder maps \({\displaystyle \mathbf {z} }\) to the reconstruction \({\displaystyle \mathbf {x'} }\) of the same shape as \({\displaystyle \mathbf {x} }\):

   $${\displaystyle \mathbf {x'} =\sigma '(\mathbf {W'z} +\mathbf {b'} )}$$

   where \({\displaystyle \mathbf {\sigma '} ,\mathbf {W'} ,{\text{ and }}\mathbf {b'} }\) for the decoder may differ in general from those of the encoder.

   Autoencoders minimize reconstruction errors, such as the L-2 loss:

   $${\displaystyle {\mathcal {L}}(\mathbf {x} ,\psi ( \phi (\mathbf {x} ) ) ) = {\mathcal {L}}(\mathbf {x} ,\mathbf {x'} )=\|\mathbf {x} -\mathbf {x'} \|^{2}=\|\mathbf {x} -\sigma '(\mathbf {W'} (\sigma (\mathbf {Wx} +\mathbf {b} ))+\mathbf {b'} )\|^{2}}$$

   where \({\displaystyle \mathbf {x} }\) is usually averaged over some input training set.
   
   

8. Applications:
   The applications of auto-encoders have changed overtime.
   This is due to the advances in the fields that auto-encoders were applied in, or to the incompetency of the auto-encoders.
   Recently, auto-encoders are applied to:
   • Data-Denoising
   • Dimensionality Reduction (for data visualization)

   With appropriate dimensionality and sparsity constraints, Autoencoders can learn data projections that are more interesting than PCA or other basic techniques.

   For 2D visualization specifically, t-SNE is probably the best algorithm around, but it typically requires relatively low-dimensional data. So a good strategy for visualizing similarity relationships in high-dimensional data is to start by using an Autoencoder to compress your data into a low-dimensional space (e.g. 32 dimensional) (by an auto-encoder), then use t-SNE for mapping the compressed data to a 2D plane.

   • Deep Autoencoders for document retrieval (Hinton)
   • Semantic Hashing (Hinton)
   • Learning binary codes for image retrieval (Hinton)
   • Shallow Autoencoders for pre-training (Hinton)
     
     
9. Types of Auto-Encoders:
   • Vanilla Auto-Encoder
   • Sparse Auto-Encoder
   • Denoising Auto-Encoder
   • Variational Auto-Encoder (VAE)
   • Contractive Auto-Encoder
     
     

10. Auto-Encoders for initializing Neural-Nets:
    After training an auto-encoder, we can use the encoder to compress the input data into it’s latent representation (which we can view as features) and input those to the neural-net (e.g. a classifier) for prediction.
    
    

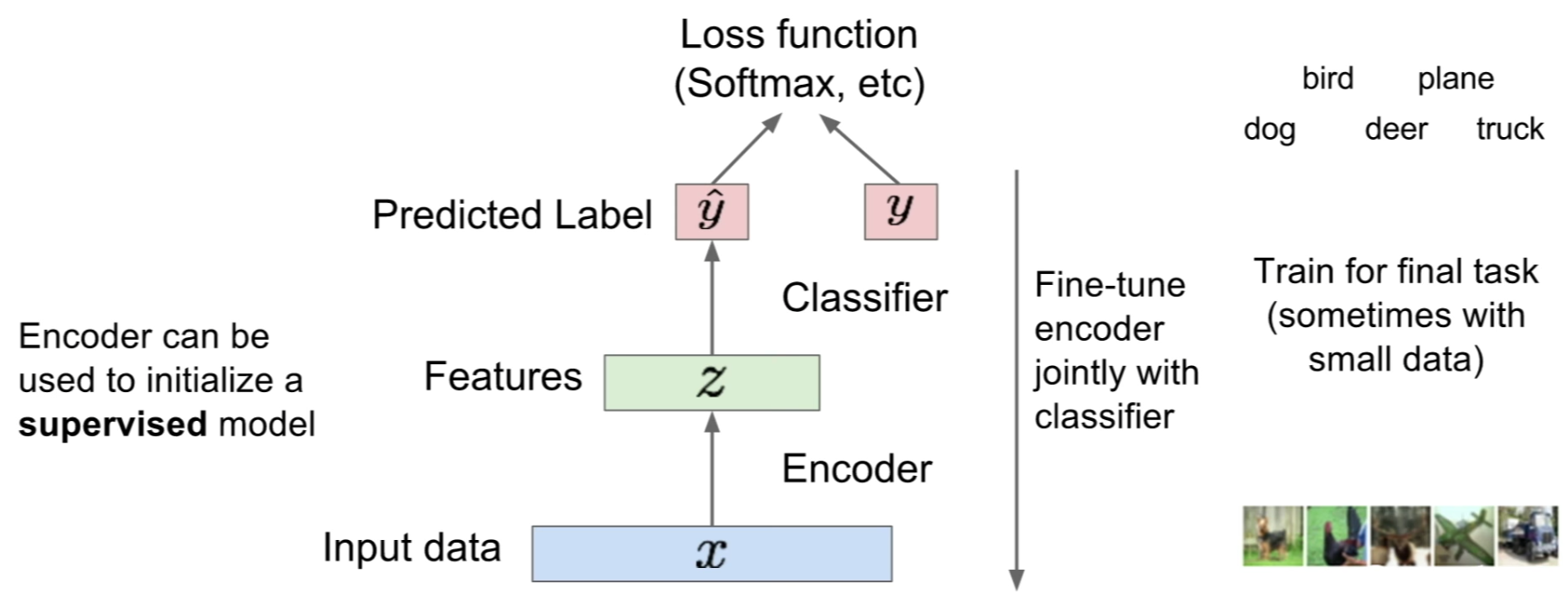
11. Representational Power, Layer Size and Depth:
    The universal approximator theorem guarantees that a feedforward neural network with at least one hidden layer can represent an approximation of any function (within a broad class) to an arbitrary degree of accuracy, provided that it has enough hidden units. This means that an Autoencoder with a single hidden layer is able to represent the identity function along the domain of the data arbitrarily well.
    However, the mapping from input to code is shallow. This means that we are not able to enforce arbitrary constraints, such as that the code should be sparse.
    A deep Autoencoder, with at least one additional hidden layer inside the encoder itself, can approximate any mapping from input to code arbitrarily well, given enough hidden units.
    
    

Notes:

• Progression of AEs (in CV?):
  • Originally: Linear + nonlinearity (sigmoid)
  • Later: Deep, fully-connected
  • Later: ReLU CNN (UpConv)

DL Book - AEs

1. Undercomplete Autoencoders:
   An Undercomplete Autoencoder is one whose code dimension is less than the input dimension.
   Learning an undercomplete representation forces the Autoencoder to capture the most salient features of the training data.
   
   

2. Challenges:
   • If an Autoencoder succeeds in simply learning to set \(\psi(\phi (x)) = x\) everywhere, then it is not especially useful.
     Instead, Autoencoders are designed to be unable to learn to copy perfectly. Usually they are restricted in ways that allow them to copy only approximately, and to copy only input that resembles the training data.
   • In Undercomplete Autoencoders If the Encoder and Decoder are allowed too much capacity, the Autoencoder can learn to perform the copying task without extracting useful information about the distribution of the data.
     Theoretically, one could imagine that an Autoencoder with a one-dimensional code but a very powerful nonlinear encoder could learn to represent each training example \(x^{(i)}\) with the code \(i\). This specific scenario does not occur in practice, but it illustrates clearly that an Autoencoder trained to perform the copying task can fail to learn anything useful about the dataset if the capacity of the Autoencoder is allowed to become too great.
   • A similar problem occurs in complete AEs
   • As well as in the overcomplete case, in which the hidden code has dimension greater than the input.
     In complete and overcomplete cases, even a linear encoder and linear decoder can learn to copy the input to the output without learning anything useful about the data distribution.
     
     

3. Regularized AutoEncoders:
   To address the challenges in learning useful representations; we introduce Regularized Autoencoders.

   Regularized Autoencoders allow us to train any architecture of Autoencoder successfully, choosing the code dimension and the capacity of the encoder and decoder based on the complexity of distribution to be modeled.

   Rather than limiting the model capacity by keeping the encoder and decoder shallow and the code size small, regularized Autoencoders use a loss function that encourages the model to have other properties besides the ability to copy its input to its output:

   • Sparsity of the representation
   • Smallness of the derivative of the representation
   • Robustness to noise or to missing inputs.

   A regularized Autoencoder can be nonlinear and overcomplete but still learn something useful about the data distribution even if the model capacity is great enough to learn a trivial identity function.
   
   

4. Generative Models as (unregularized) Autoencoders:
   In addition to the traditional AEs described here, nearly any generative model with latent variables and equipped with an inference procedure (for computing latent representations given input) may be viewed as a particular form of Autoencoder; most notably the descendants of the Helmholtz machine (Hinton et al., 1995b), such as:
   • Variational Autoencoders
   • Generative Stochastic Networks

   These models naturally learn high-capacity, overcomplete encodings of the input and do NOT require regularization for these encodings to be useful. Their encodings are naturally useful because the models were trained to approximately maximize the probability of the training data rather than to copy the input to the output.
   
   

5. Stochastic Encoders and Decoders:
   Discussion
   
   

Regularized Autoencoders

1. Sparse Autoencoders:
   Sparse Autoencoders are simply Autoencoders whose training criterion involves a sparsity penalty \(\Omega(\boldsymbol{h})\) on the code layer \(\boldsymbol{h},\) in addition to the reconstruction error:

   $${\displaystyle {\mathcal {L}}(\mathbf {x} ,\psi ( \phi (\mathbf {x} ) ) ) + \Omega(\boldsymbol{h})}$$

   where typically we have \(\boldsymbol{h}=\phi(\boldsymbol{x})\), the encoder output.

   Regularization Interpretation:
   We can think of the penalty \(\Omega(\boldsymbol{h})\) simply as a regularizer term added to a feedforward network whose primary task is to copy the input to the output (unsupervised learning objective) and possibly also perform some supervised task (with a supervised learning objective) that depends on these sparse features.

   Bayesian Interpretation of Regularization:
   Unlike other regularizers such as weight decay, there is not a straightforward Bayesian interpretation to this regularizer.
   Regularized Autoencoders defy such an interpretation because the regularizer depends on the data and is therefore by definition not a prior in the formal sense of the word.
   We can still think of these regularization terms as implicitly expressing a preference over functions.

   Latent Variable Interpretation:
   Rather than thinking of the sparsity penalty as a regularizer for the copying task, we can think of the entire sparse Autoencoder framework as approximating maximum likelihood training of a generative model that has latent variables.

   Correspondence between Sparsity and a Directed Probabilistic Model:
   Suppose we have a model with visible variables \(\boldsymbol{x}\) and latent variables \(\boldsymbol{h},\) with an explicit joint distribution \(p_{\text {model }}(\boldsymbol{x}, \boldsymbol{h})=p_{\text {model }}(\boldsymbol{h}) p_{\text {model }}(\boldsymbol{x} \vert \boldsymbol{h}) .\) We refer to \(p_{\text {model }}(\boldsymbol{h})\) as the model’s prior distribution over the latent variables, representing the model’s beliefs prior to seeing \(\boldsymbol{x}\)¹.
   The log-likelihood can be decomposed as:

   $$\log p_{\text {model }}(\boldsymbol{x})=\log \sum_{\boldsymbol{h}} p_{\text {model }}(\boldsymbol{h}, \boldsymbol{x})$$

   We can think of the Autoencoder as approximating this sum with a point estimate for just one highly likely value for \(\boldsymbol{h}\).
   This is similar to the sparse coding generative model (section 13.4), but with \(\boldsymbol{h}\) being the output of the parametric encoder rather than the result of an optimization that infers the most likely \(\boldsymbol{h}\). From this point of view, with this chosen \(\boldsymbol{h}\), we are maximizing:

   $$\log p_{\text {model }}(\boldsymbol{h}, \boldsymbol{x})=\log p_{\text {model }}(\boldsymbol{h})+\log p_{\text {model }}(\boldsymbol{x} \vert \boldsymbol{h})$$

   The \(\log p_{\text {model }}(\boldsymbol{h})\) term can be sparsity-inducing. For example, the Laplace prior,

   $$p_{\text {model }}\left(h_{i}\right)=\frac{\lambda}{2} e^{-\lambda\left|h_{i}\right|}$$

   corresponds to an absolute value sparsity penalty.
   Expressing the log-prior as an absolute value penalty, we obtain

   $$\begin{aligned} \Omega(\boldsymbol{h}) &=\lambda \sum_{i}\left|h_{i}\right| \\-\log p_{\text {model }}(\boldsymbol{h}) &=\sum_{i}\left(\lambda\left|h_{i}\right|-\log \frac{\lambda}{2}\right)=\Omega(\boldsymbol{h})+\text { const } \end{aligned}$$

   where the constant term depends only on \(\lambda\) and not \(\boldsymbol{h} .\) We typically treat \(\lambda\) as a hyperparameter and discard the constant term since it does not affect the parameter learning.
   Other priors such as the Student-t prior can also induce sparsity.
   From this point of view of sparsity as resulting from the effect of \(p_{\text {model}}(\boldsymbol{h})\) on approximate maximum likelihood learning, the sparsity penalty is not a regularization term at all. It is just a consequence of the model’s distribution over its latent variables. This view provides a different motivation for training an Autoencoder: it is a way of approximately training a generative model. It also provides a different reason for why the features learned by the Autoencoder are useful: they describe the latent variables that explain the input.

   Correspondence between Sparsity and an Undirected Probabilistic Model:
   Early work on sparse Autoencoders (Ranzato et al., 2007a, 2008) explored various forms of sparsity and proposed a connection between the sparsity penalty and the log \(Z\) term that arises when applying maximum likelihood to an undirected probabilistic model \(p(\boldsymbol{x})=\frac{1}{Z} \tilde{p}(\boldsymbol{x})\).
   The idea is that minimizing \(\log Z\) prevents a probabilistic model from having high probability everywhere, and imposing sparsity on an Autoencoder prevents the Autoencoder from having low reconstruction error everywhere. In this case, the connection is on the level of an intuitive understanding of a general mechanism rather than a mathematical correspondence.

   The interpretation of the sparsity penalty as corresponding to \(\log p_{\text {model }}(\boldsymbol{h})\) in a directed model \(p_{\text {model}}(\boldsymbol{h}) p_{\text {model}} \left(\boldsymbol{x} \vert \boldsymbol{h}\right)\) is more mathematically straightforward.

   Achieving actual zeros in \(\boldsymbol{h}\):
   One way to achieve actual zeros in \(\boldsymbol{h}\) for sparse (and denoising) Autoencoders was introduced in Glorot et al. (2011b). The idea is to use rectified linear units to produce the code layer. With a prior that actually pushes the representations to zero (like the absolute value penalty), one can thus indirectly control the average number of zeros in the representation.

   Notes:

   • Sparse Autoencoder and Unsupervised Feature Learning #1 (Ng)
   • Sparse Autoencoder and Unsupervised Feature Learning #2 (Ng)
     
     
2. Denoising Autoencoders:
   Denoising Autoencoders (DAEs) is an Autoencoder that receives a corrupted data point as input and is trained to predict the original, uncorrupted data point as its output.
   It minimizes:

   $$L(\boldsymbol{x}, g(f(\tilde{\boldsymbol{x}})))$$

   where \(\tilde{\boldsymbol{x}}\) is a copy of \(\boldsymbol{x}\) that has been corrupted by some form of noise.

   Denoising Autoencoders must therefore learn to undo this corruption rather than simply copying their input.
   Denoising training forces \(\psi\) and \(\phi\) to implicitly learn the structure of \(p_{\text {data}}(\boldsymbol{x}),\) as shown by Alain and Bengio (2013) and Bengio et al. (2013c).
   - Provide yet another example of how useful properties can emerge as a byproduct of minimizing reconstruction error.
   - Also an example of, how overcomplete, high-capacity models may be used as Autoencoders so long as care is taken to prevent them from learning the identity function.

   We introduce a corruption process \(C(\tilde{\mathbf{x}} \vert \mathbf{x})\) which represents a conditional distribution over corrupted samples \(\tilde{\boldsymbol{x}}\), given a data sample \(\boldsymbol{x}\).
   The Autoencoder then learns a reconstruction distribution \(p_{\text {reconstruct}}(\mathrm{x} \vert \tilde{\mathrm{x}})\) estimated from training pairs \((\boldsymbol{x}, \tilde{\boldsymbol{x}}),\) as follows:

   • Sample a training example \(\boldsymbol{x}\) from the training data.
   • Sample a corrupted version \(\tilde{\boldsymbol{x}}\) from \(C(\tilde{\mathbf{x}} \vert \mathbf{x}=\boldsymbol{x})\)
   • Use \((\boldsymbol{x}, \tilde{\boldsymbol{x}})\) as a training example for estimating the Autoencoder reconstruction distribution \(p_{\text {reconstruct}}(\boldsymbol{x} \vert \tilde{\boldsymbol{x}})=p_{\text {decoder}}(\boldsymbol{x} \vert \boldsymbol{h})\) with \(\boldsymbol{h}\) the output of encoder \(f(\tilde{\boldsymbol{x}})\) and \(p_{\text {decoder}}\) typically defined by a decoder \(g(\boldsymbol{h})\).

   Learning:
   Typically we can simply perform gradient-based approximate minimization (such as minibatch gradient descent) on the negative log-likelihood \(-\log p_{\text {decoder}}(\boldsymbol{x} \vert \boldsymbol{h})\).
   So long as the encoder is deterministic, the denoising Autoencoder is a feedforward network and may be trained with exactly the same techniques as any other FFN.
   We can therefore view the DAE as performing stochastic gradient descent on the following expectation:

   $$-\mathbb{E}_{\mathbf{x} \sim \hat{p}_{\text {data }}(\mathbf{x})} \mathbb{E}_{\tilde{\mathbf{x}} \sim C(\tilde{\mathbf{x}} \vert \boldsymbol{x})} \log p_{\text {decoder}}(\boldsymbol{x} \vert \boldsymbol{h}=f(\tilde{\boldsymbol{x}}))$$

   where \(\hat{p}_ {\text {data}}(\mathrm{x})\) is the training distribution.

   Score Matching - Estimating the Score:
   Score Matching (Hyvärinen, 2005) is an alternative to maximum likelihood. It provides a consistent estimator of probability distributions based on encouraging the model to have the same score as the data distribution at every training point \(\boldsymbol{x}\). In this context, the score is a particular gradient field

   $$\nabla_{\boldsymbol{x}} \log p(\boldsymbol{x})$$

   For Autoencoders, it is sufficient to understand that learning the gradient field of \(\log p_{\text {data}}\) is one way to learn the structure of \(p_{\text {data itself}}\).

   A very important property of DAEs is that their training criterion (with \(\text { conditionally Gaussian } p(\boldsymbol{x} \vert \boldsymbol{h}))\) makes the Autoencoder learn a vector field \((f(\boldsymbol{x}))-\boldsymbol{x}\)) that estimates the score of the data distribution.
   Vector Field Learning and the Score of \(p_{\text{data}}\)
   Continuous Valued \(\boldsymbol{x}\):
   For continuous-valued \(\boldsymbol{x}\), the denoising criterion with Gaussian corruption and reconstruction distribution yields an estimator of the score that is applicable to general encoder and decoder parametrizations (Alain and Bengio, 2013).
   This means a generic encoder-decoder architecture may be made to estimate the score by training with the squared error criterion,

   $$\|g(f(\tilde{x}))-x\|^{2}$$

   and corruption,

   $$C(\tilde{\mathbf{x}}=\tilde{\boldsymbol{x}} \vert \boldsymbol{x})=\mathcal{N}\left(\tilde{\boldsymbol{x}} ; \mu=\boldsymbol{x}, \Sigma=\sigma^{2} I\right)$$

   with noise variance \(\sigma^{2}\).
   Illustration for continuous \(\boldsymbol{x}\)
   Guarantees:
   In general, there is no guarantee that the reconstruction \(g(f(\boldsymbol{x}))\) minus the input \(\boldsymbol{x}\) corresponds to the gradient of any function, let alone to the score. That is why the early results (Vincent, 2011) are specialized to particular parametrizations where \(g(f(\boldsymbol{x}))-\boldsymbol{x}\) may be obtained by taking the derivative of another function. Kamyshanska and Memisevic \((2015)\) generalized the results of Vincent \((2011)\) by identifying a family of shallow Autoencoders such that \(g(f(\boldsymbol{x}))-\boldsymbol{x}\) corresponds to a score for all members of the family.

   DAEs as representing Probability Distributions and Variational AEs:
   So far we have described only how the DAE learns to represent a probability distribution. More generally, one may want to use the Autoencoder as a generative model and draw samples from this distribution. This is knows as the Variational Autoencoder.

   Denoising AutoEncoders and RBMs:
   Denoising training of a specific kind of Autoencoder (sigmoidal hidden units, linear reconstruction units) using Gaussian noise and mean squared error as the reconstruction cost is equivalent (Vincent, 2011) to training a specific kind of undirected probabilistic model called an RBM with Gaussian visible units. This kind of model will be described in detail in section 20.5.1; for the present discussion it suffices to know that it is a model that provides an explicit \(p_{\text {model }}(\boldsymbol{x} ; \boldsymbol{\theta})\). When the RBM is trained using denoising score matching (Kingma and LeCun, 2010), its learning algorithm is equivalent to denoising training in the corresponding Autoencoder. With a fixed noise level, regularized score matching is not a consistent estimator; it instead recovers a blurred version of the distribution. However, if the noise level is chosen to approach \(0\) when the number of examples approaches infinity, then consistency is recovered. Denoising score matching is discussed in more detail in section 18.5.
   Other connections between Autoencoders and RBMs exist. Score matching applied to RBMs yields a cost function that is identical to reconstruction error combined with a regularization term similar to the contractive penalty of the CAE (Swersky et al., 2011). Bengio and Delalleau (2009) showed that an Autoencoder gradient provides an approximation to contrastive divergence training of RBMs.

   Historical Perspective:
   Discussion
   
   

3. Regularizing by Penalizing Derivatives:
   Another strategy for regularizing an Autoencoder is to use a penalty \(\Omega\) as in sparse Autoencoders,

   $$L(\boldsymbol{x}, g(f(\boldsymbol{x})))+\Omega(\boldsymbol{h}, \boldsymbol{x})$$

   but with a different form of \(\Omega\):

   $$\Omega(\boldsymbol{h}, \boldsymbol{x})=\lambda \sum_{i}\left\|\nabla_{\boldsymbol{x}} h_{i}\right\|^{2}$$

   This forces the model to learn a function that does not change much when \(\boldsymbol{x}\) changes slightly. Because this penalty is applied only at training examples, it forces the Autoencoder to learn features that capture information about the training distribution.
   An Autoencoder regularized in this way is called a contractive Autoencoder (CAE). This approach has theoretical connections to denoising Autoencoders, manifold learning and probabilistic modeling.
   
   

4. Contractive Autoencoders:
   Contractive Autoencoders (CAEs) (Rifai et al., 2011a,b) introduces an explicit regularizer on the code \(\boldsymbol{h}=\phi(\boldsymbol{x}),\) encouraging the derivatives of \(\phi\) to be as small as possible:

   $$\Omega(\boldsymbol{h})=\lambda\left\|\frac{\partial \phi(\boldsymbol{x})}{\partial \boldsymbol{x}}\right\|_ {F}^{2}$$

   The penalty \(\Omega(\boldsymbol{h})\) is the squared Frobenius norm (sum of squared elements) of the Jacobian matrix of partial derivatives associated with the encoder function.

   Connection to Denoising Autoencoders:
   There is a connection between the denoising Autoencoder and the contractive Autoencoder: Alain and Bengio (2013) showed that in the limit of small Gaussian input noise, the denoising reconstruction error is equivalent to a contractive penalty on the reconstruction function that maps \(\boldsymbol{x}\) to \(\boldsymbol{r}=\psi(\phi(\boldsymbol{x}))\).
   In other words:
   - Denoising Autoencoders: make the reconstruction function resist small but finite-sized perturbations of the input
   - Contractive Autoencoders: make the feature extraction function resist infinitesimal perturbations of the input.
   When using the Jacobian-based contractive penalty to pretrain features \(\phi(\boldsymbol{x})\) for use with a classifier, the best classification accuracy usually results from applying the contractive penalty to \(\phi(\boldsymbol{x})\) rather than to \(\psi(\phi(\boldsymbol{x}))\).
   A contractive penalty on \(\phi(\boldsymbol{x})\) also has close connections to score matching.

   Contractive - Definition and Analysis:
   The name contractive arises from the way that the CAE warps space. Specifically, because the CAE is trained to resist perturbations of its input, it is encouraged to map a neighborhood of input points to a smaller neighborhood of output points. We can think of this as contracting the input neighborhood to a smaller output neighborhood.

   To clarify, the CAE is contractive only locally-all perturbations of a training point \(\boldsymbol{x}\) are mapped near to \(\phi(\boldsymbol{x})\). Globally, two different points \(\boldsymbol{x}\) and \(\boldsymbol{x}^{\prime}\) may be mapped to \(\phi(\boldsymbol{x})\) and \(\psi\left(\boldsymbol{x}^{\prime}\right)\) points that are farther apart than the original points.

   As a linear operator:
   We can think of the Jacobian matrix \(J\) at a point \(x\) as approximating the nonlinear encoder \(\phi(x)\) as being a linear operator. This allows us to use the word “contractive” more formally.
   In the theory of linear operators, a linear operator is said to be contractive if the norm of \(J x\) remains less than or equal to 1 for all unit-norm \(x\). In other words, \(J\) is contractive if it shrinks the unit sphere.
   We can think of the CAE as penalizing the Frobenius norm of the local linear approximation of \(\phi(x)\) at every training point \(x\) in order to encourage each of these local linear operator to become a contraction.

   Manifold Learning:
   Regularized Autoencoders learn manifolds by balancing two opposing forces.
   In the case of the CAE, these two forces are reconstruction error and the contractive penalty \(\Omega(\boldsymbol{h}) .\) Reconstruction error alone would encourage the CAE to learn an identity function. The contractive penalty alone would encourage the CAE to learn features that are constant with respect to \(\boldsymbol{x}\).
   The compromise between these two forces yields an Autoencoder whose derivatives \(\frac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{x}}\) are mostly tiny. Only a small number of hidden units, corresponding to a small number of directions in the input, may have significant derivatives.

   The goal of the CAE is to learn the manifold structure of the data.
   Directions \(x\) with large \(J x\) rapidly change \(h,\) so these are likely to be directions which approximate the tangent planes of the manifold.
   Experiments by Rifai et al. (2011 a,b) show that training the CAE results in:

   1. Most singular values of \(J\) dropping below \(1\) in magnitude and therefore becoming contractive
   2. However, some singular values remain above \(1,\) because the reconstruction error penalty encourages the CAE to encode the directions with the most local variance.
   • The directions corresponding to the largest singular values are interpreted as the tangent directions that the contractive Autoencoder has learned.
   • Visualizations of the experimentally obtained singular vectors do seem to correspond to meaningful transformations of the input image.
     Since, Ideally, these tangent directions should correspond to real variations in the data.
     For example, a CAE applied to images should learn tangent vectors that show how the image changes as objects in the image gradually change pose.
     Estimated Tangent Vectors of the Manifold

   Issues with Contractive Penalties:
   Although it is cheap to compute the CAE regularization criterion, in the case of a single hidden layer Autoencoder, it becomes much more expensive in the case of deeper Autoencoders.
   The strategy followed by Rifai et al. (2011a) is to:
   - Separately train a series of single-layer Autoencoders, each trained to reconstruct the previous Autoencoder’s hidden layer.
   - The composition of these Autoencoders then forms a deep Autoencoder.

   • Because each layer was separately trained to be locally contractive, the deep Autoencoder is contractive as well.
   • The result is not the same as what would be obtained by jointly training the entire architecture with a penalty on the Jacobian of the deep model, but it captures many of the desirable qualitative characteristics.

   Another issue is that the contractive penalty can obtain useless results if we do not impose some sort of scale on the decoder.
   - For example, the encoder could consist of multiplying the input by a small constant \(\epsilon\) and the decoder could consist of dividing the code by \(\epsilon\).
   As \(\epsilon\) approaches \(0\), the encoder drives the contractive penalty \(\Omega(\boldsymbol{h})\) to approach \(0\) without having learned anything about the distribution.
   Meanwhile, the decoder maintains perfect reconstruction.
   - In Rifai et al. (2011a), this is prevented by tying the weights of \(\phi\) and \(\psi\). Both \(\phi\) and \(\psi\) are standard neural network layers consisting of an affine transformation followed by an element-wise nonlinearity, so it is straightforward to set the weight matrix of \(\psi\) to be the transpose of the weight matrix of \(\phi\).

5. Predictive Sparse Decomposition:
   Discussion

Learning Manifolds with Autoencoders

PDF