K-Nearest Neighbors (k-NN)

1. KNN:
   KNN is a non-parametric method used for classification and regression.
   It is based on the Local Constancy (Smoothness) Prior, which states that “the function we learn should not change very much within a small region.”, for generalization.
   • K-Means & Local Constancy

   
   

2. Structure:
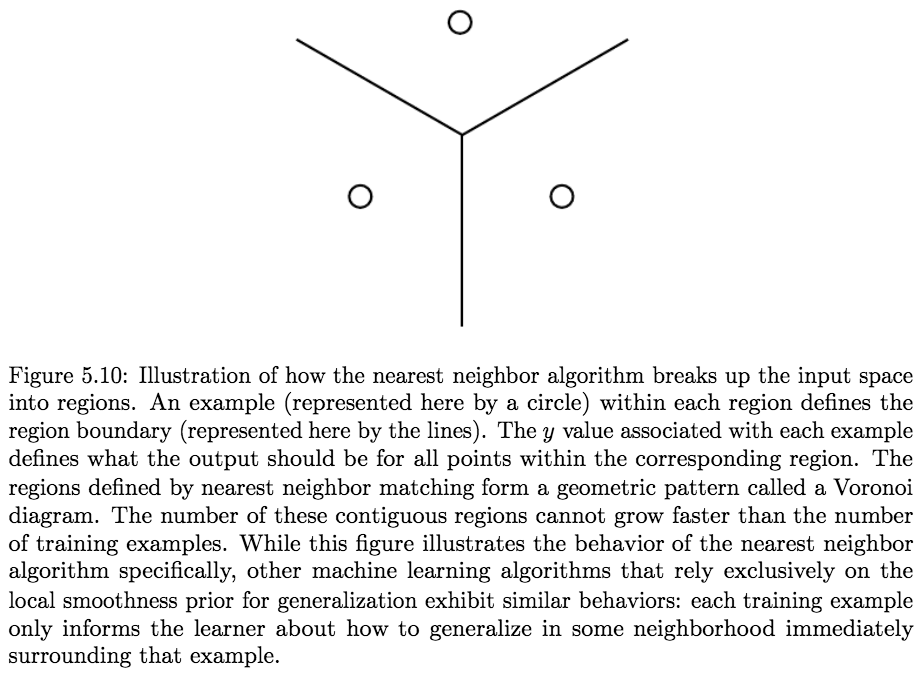
   In both classification and regression, the input consists of the \(k\) closest training examples in the feature space. The output depends on whether k-NN is used for classification or regression:
   • In k-NN classification, the output is a class membership. An object is classified by a plurality vote of its neighbors, with the object being assigned to the class most common among its \(k\) nearest neighbors (\(k\) is a positive integer, typically small). If \(k = 1\), then the object is simply assigned to the class of that single nearest neighbor.
   • In k-NN regression, the output is the property value for the object. This value is the average of the values of \(k\) nearest neighbors.
     
     

3. Formal Description - Statistical Setting:
   Suppose we have pairs \({\displaystyle (X_{1},Y_{1}),(X_{2},Y_{2}),\dots ,(X_{n},Y_{n})}\) taking values in \({\displaystyle \mathbb {R} ^{d}\times \{1,2\}}\), where \(Y\) is the class label of \(X\), so that \({\displaystyle X|Y=r\sim P_{r}}\) for \({\displaystyle r=1,2}\) (and probability distributions \({\displaystyle P_{r}}\). Given some norm \({\displaystyle \|\cdot \|}\) on \({\displaystyle \mathbb {R} ^{d}}\) and a point \({\displaystyle x\in \mathbb {R} ^{d}}\), let \({\displaystyle (X_{(1)},Y_{(1)}),\dots ,(X_{(n)},Y_{(n)})}\) be a reordering of the training data such that \({\displaystyle \|X_{(1)}-x\|\leq \dots \leq \|X_{(n)}-x\|}\).
   
   

4. Choosing \(k\):
   Nearest neighbors can produce very complex decision functions, and its behavior is highly dependent on the choice of \(k\):
   

   Choosing \(k = 1\), we achieve an optimal training error of \(0\) because each training point will classify as itself, thus achieving \(100\%\) accuracy on itself.
   However, \(k = 1\) overfits to the training data, and is a terrible choice in the context of the bias-variance tradeoff.

   Increasing \(k\) leads to increase in training error, but a decrease in testing error and achieves better generalization.

   At one point, if \(k\) becomes too large, the algorithm will underfit the training data, and suffer from huge bias.

   In general, we select \(k\) using cross-validation.

   

   \[\text{Training and Test Errors as a function of } k \:\:\:\:\:\:\:\:\:\:\:\:\]

   
   

5. Bias-Variance Decomposition of k-NN:
   PDF (189)

   
   

6. Properties:
   • Computational Complexity:
     • We require \(\mathcal{O}(n)\) space to store a training set of size \(n\). There is no runtime cost during training if we do not use specialized data structures to store the data.
       However, predictions take \(\mathcal{O}(n)\) time, which is costly.
     • There has been research into Approximate Nearest Neighbors (ANN) procedures that quickly find an approximation for the nearest neighbor - some common ANN methods are Locality-Sensitive Hashing and algorithms that perform dimensionality reduction via randomized (Johnson-Lindenstrauss) distance-preserving projections.
     • k-NN is a type of instance-based learning, or “lazy learning”, where the function is only approximated locally and all computation is deferred until classification.
   • Flexibility:
     • When \(k>1,\) k-NN can be modified to output predicted probabilities \(P(Y \vert X)\) by defining \(P(Y \vert X)\) as the proportion of nearest neighbors to \(X\) in the training set that have class \(Y\).
     • k-NN can also be adapted for regression — instead of taking the majority vote, take the average of the \(y\) values for the nearest neighbors.
     • k-NN can learn very complicated, non-linear decision boundaries (highly influenced by choice of \(k\)).
   • Non-Parametric(ity):
     k-NN is a non-parametric method, which means that the number of parameters in the model grows with \(n\), the number of training points. This is as opposed to parametric methods, for which the number of parameters is independent of \(n\).
   • High-dimensional Behavior:
     • k-NN does NOT behave well in high dimensions.
       As the dimension increases, data points drift farther apart, so even the nearest neighbor to a point will tend to be very far away.
     • It is sensitive to the local structure of the data (in any/all dimension/s).
   • Theoretical Guarantees/Properties:
     \(1\)-NN has impressive theoretical guarantees for such a simple method:
     • Cover and Hart, 1967 prove that as the number of training samples \(n\) approaches infinity, the expected prediction error for \(1-\mathrm{NN}\) is upper bounded by \(2 \epsilon^{*}\), where \(\epsilon^{*}\) is the Bayes (optimal) error.
     • Fix and Hodges, 1951 prove that as \(n\) and \(k\) approach infinity and if \(\frac{k}{n} \rightarrow 0\), then the \(k\) nearest neighbor error approaches the Bayes error.
       
       
7. Algorithm and Computational Complexity:
   Training:
   • Algorithm: To train this classifier, we simply store our training data for future reference.
     Sometimes we store the data in a specialized structure called a k-d tree. This data structure usually allows for faster (average-case \(\mathcal{O}(\log n)\)) nearest neighbors queries.

     For this reason, k-NN is sometimes referred to as “lazy learning”.

   • Complexity: \(\:\:\:\:\mathcal{O}(1)\)

   Prediction:

   • Algorithm:
     1. Compute the \(k\) closest training data points (“nearest neighbors”) to input point \(\boldsymbol{z}\).
        “Closeness” is quantified using some metric; e.g. Euclidean distance.
     2. Assignment Stage:
        • Classification: Find the most common class \(y\) among these \(k\) neighbors and classify \(\boldsymbol{z}\) as \(y\) (majority vote)
        • Regression: Take the average label of the \(k\) nearest points.
   • Complexity: \(\:\:\:\:\mathcal{O}(N)\)
     
     

   Notes:

   • We choose odd \(k\) for binary classification to break symmetry of majority vote
     
     

8. Behavior in High-Dimensional Space - Curse of Dimensionality:
   As mentioned, k-NN does NOT perform well in high-dimensional space. This is due to the “Curse of Dimensionality”.

   Curse of Dimensionality (CoD):
   To understand CoD, we first need to understand the properties of metric spaces. In high-dimensional spaces, much of our low-dimensional intuition breaks down:

   Geometry of High-Dimensional Space:
   Consider a ball in \(\mathbb{R}^d\) centered at the origin with radius \(r\), and suppose we have another ball of radius \(r - \epsilon\) centered at the origin. In low dimensions, we can visually see that much of the volume of the outer ball is also in the inner ball.
   In general, the volume of the outer ball is proportional to \(r^{d}\), while the volume of the inner ball is proportional to \((r-\epsilon)^{d}\).
   Thus the ratio of the volume of the inner ball to that of the outer ball is:

   $$\frac{(r-\epsilon)^{d}}{r^{d}}=\left(1-\frac{\epsilon}{r}\right)^{d} \approx e^{-\epsilon d / r} \underset{d \rightarrow \infty}{\longrightarrow} 0$$

   Hence as \(d\) gets large, most of the volume of the outer ball is concentrated in the annular region \(\{x : r-\epsilon < x < r\}\) instead of the inner ball.
   

   Concentration of Measure:
   High dimensions also make Gaussian distributions behave counter-intuitively. Suppose \(X \sim\) \(\mathcal{N}\left(0, \sigma^{2} I\right)\). If \(X_{i}\) are the components of \(X\) and \(R\) is the distance from \(X\) to the origin, then \(R^{2}=\sum_{i=1}^{d} X_{i}^{2}\). We have \(\mathbb{E}\left[R^{2}\right]=d \sigma^{2},\) so in expectation a random Gaussian will actually be reasonably far from the origin. If \(\sigma=1,\) then \(R^{2}\) is distributed chi-squared with \(d\) degrees of freedom.
   One can show that in high dimensions, with high probability \(1-\mathcal{O}\left(e^{-d^{\epsilon}}\right)\), this multivariate Gaussian will lie within the annular region \(\left\{X :\left|R^{2}-\mathbb{E}\left[R^{2}\right]\right| \leq d^{1 / 2+\epsilon}\right\}\) where \(\mathbb{E}\left[R^{2}\right]=d \sigma^{2}\) (one possible approach is to note that as \(d \rightarrow \infty,\) the chi-squared approaches a Gaussian by the CLT, and use a Chernoff bound to show exponential decay). This phenomenon is known as Concentration of Measure.

   Without resorting to more complicated inequalities, we can show a simple, weaker result:
   \(\bf{\text{Theorem:}}\) \(\text{If } X_{i} \sim \mathcal{N}\left(0, \sigma^{2}\right), i=1, \ldots, d \text{ are independent and } R^{2}=\sum_{i=1}^{d} X_{i}^{2}, \text{ then for every } \epsilon>0, \\ \text{the following holds: }\)

   $$\lim_{d \rightarrow \infty} P\left(\left|R^{2}-\mathbb{E}\left[R^{2}\right]\right| \geq d^{\frac{1}{2}+\epsilon}\right)=0$$

   Thus in the limit, the squared radius is concentrated about its mean.

   Proof.

   Thus a random Gaussian will lie within a thin annular region away from the origin in high dimensions with high probability, even though the mode of the Gaussian bell curve is at the origin. This illustrates the phenomenon in high dimensions where random data is spread very far apart.

   The k-NN classifier was conceived on the principle that nearby points should be of the same class - however, in high dimensions, even the nearest neighbors that we have to a random test point will tend to be far away, so this principle is no longer useful.
   
   

9. Improving k-NN:
   (1) Obtain More Training Data:
   More training data allows us to counter-act the sparsity in high-dimensional space.

   (2) Dimensionality Reduction - Feature Selection and Feature Projection:
   Reduce the dimensionality of the features and/or pick better features. The best way to counteract the curse of dimensionality.

   (3) Different Choices of Metrics/Distance Functions:
   We can modify the distance function. E.g.

   • The family of Minkowski Distances that are induced by the \(L^p\) norms:

     $$D_{p}(\mathbf{x}, \mathbf{z})=\left(\sum_{i=1}^{d}\left|x_{i}-z_{i}\right|^{p}\right)^{\frac{1}{p}}$$

     Without preprocessing the data, \(1-\mathrm{NN}\) with the \(L^{3}\) distance outperforms \(1-\mathrm{NN}\) with \(L^{2}\) on MNIST.

   • We can, also, use kernels to compute distances in a different feature space.
     For example, if \(k\) is a kernel with associated feature map \(\Phi\) and we want to compute the Euclidean distance from \(\Phi(x)\) to \(\Phi(z)\), then we have:

     $$\begin{aligned}\|\Phi(\mathbf{x})-\Phi(\mathbf{z})\|_ {2}^{2} &=\Phi(\mathbf{x})^{\top} \Phi(\mathbf{x})-2 \Phi(\mathbf{x})^{\top} \Phi(\mathbf{z})+\Phi(\mathbf{z})^{\top} \Phi(\mathbf{z}) \\ &=k(\mathbf{x}, \mathbf{x})-2 k(\mathbf{x}, \mathbf{z})+k(\mathbf{z}, \mathbf{z}) \end{aligned}$$

     Thus if we define \(D(\mathrm{x}, \mathrm{z})=\sqrt{k(\mathrm{x}, \mathrm{x})-2 k(\mathrm{x}, \mathrm{z})+k(\mathrm{z}, \mathrm{z})}\) , then we can perform Euclidean nearest neighbors in \(\mathrm{\Phi}\)-space without explicitly representing \(\Phi\) by using the kernelized distance function \(D\).